Корреляционно- регрессионный анализ

5.

Различают два типа связей между различными явлениями и их признаками: функциональную (жестко детерминированную) и статистическую (стохастические детерминированную). Строго определить различие этих типов связи можно тогда, когда они получают математическую формулировку. ∆ связь двух явлений (признаков)

Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними является функциональной. ∆ 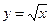→ значению х=4 соответствует не одно, а два значения у (у₁=2 и у=-2).

Если с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения с некоторыми вероятностями, но ее среднее значение изменяются по определенному закону – связь является статистической (стохастической). При статистической связи разным значениям одной переменной соответствуют разные распределения значений другой переменной.

В анализе финансово-хозяйственной деятельности стохастические модели используются, когда необходимо:

- оценить влияние факторов, по которым нельзя построить жестко детерминированную модель;

- изучить и сравнить влияние факторов, которые невозможно включить в одну и ту же детерминированную модель;

- выделить и оценить влияние сложных факторов, которые не могут быть выражены одним определенным количественным показателем (∆ пол, образование, занятие, семейное состояние человека, отрасль, форма собственности предприятия, т.е. признаки не имеющие количественного выражения).

Условия применения стохастического подхода:

- необходимо наличие достаточно большой совокупности объектов (детерминированную модель можно анализировать и строить по одному объекту);

- необходим достаточный объем наблюдений (считается, что при построении регрессии количество наблюдений должно в 6-8 раз превышать количество факторов, что крайне редко встречается в АФХДП);

- наличие случайности наблюдений.

В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода распространены в экономических исследованиях.

Стохастическое моделирование предназначено для решения трех основных задач:

1. установление самого факта наличия (отсутствия) связи между признаками;

2. прогнозирование неизвестных значений результативных показателей по заданным значениям факторных признаков;

3. измерение тесноты связи между показателями и сравнительный анализ степени их влияния.

Этапы стохастического моделирования.

Этап 1 – качественный анализ:

■ постановка цели анализа;

■ определение совокупности данных;

■ определение результативных признаков;

■ выбор периода анализа;

■ определение факторных признаков:

▪ 1. признаки-факторы должны находиться в причинной связи с результативным признаком. Поэтому, недопустимо, например, в модель ПТ (у) вводить в качестве одного из факторов (x_j) средний разряд рабочих, хотя включение такого фактора значительно повышает коэффициент корреляции;

▪ 2. признаки-факторы не должны дублировать друг друга 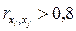→ не следует включать в модель ПТ и энерговооруженность рабочих и их фондовооруженность, так как эти факторы тесно связаны друг с другом в большинстве объектов;

▪ 3. не следует включать в модель факторы разных уровней иерархии. ∆ в модель себестоимости продукции не следует включать и платежеспособный спрос населения, и цену продукции, и т.е. субфактор самого спроса;

▪ 4. желательно, чтобы между результативным и факторными признаками соблюдалось единство совокупности, к которой они отнесены, т.е. ∆ у - средняя заработная плата рабочего, то х_i – должны относиться к рабочему: разряд, стаж, возраст, энерговооруженность рабочего и т.д. Правило это не категорическое (в модель можно включить и уровень специализации предприятия)

Этап 2 – предварительный анализ моделируемой совокупности:

■ проверка однородности совокупности (Var < 33%), если совокупность неоднородна следует исключать из нее «аномальные» наблюдения, поскольку они, скорее всего, нетипичны для данного исследования;

■ исключение «аномальных» наблюдений (наблюдение признается аномальным и исключается, если его отклонение от средней (х_i - 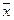) более чем в 3 раза превышает среднеквадратическое отклонение выборки σ;

■ установление законов распределения изучаемых переменных. В условиях малых выборок проверка нормальности распределений признаков проводится путем сравнения эмпирических коэффициентов асимметрии и эксцесса с их средними квадратическими ошибками (σ_As и σ_Ex соответственно). Нормальность распределения подтверждается, если выполнены неравенства: │As│<3σ_As и │Ex│<3σ_Ex.

Этап 3 – построение регрессионной модели экономического объекта:

■ перебор конкурирующих вариантов моделей (как правило, осуществляется с использованием компьютера);

■ уточнение перечня факторов, включаемых в модель (например, путем расчета парных коэффициентов корреляции). Факторы x_i и x_j включаются в модель вида y=f (x₁, x₂,…, x_n) одновременно, есл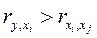и:

и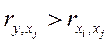

■ расчет оценок параметров уравнения регрессии.

Этап 4 – экономическая интерпретация и практическое использование модели

■ определение пространственно-временной устойчивости зависимостей. Проверка устойчивости модели осуществляется расчетом ее параметров на усеченной или расширенной совокупности, а также по той же совокупности, но в другом временном интервале;

■ оценка прогностических свойств модели.

Корреляционный анализ есть метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными. Особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее тесноты, не вскрывая ее причин.

В статистике теснота связи может определяться с помощью различных коэффициентов (Фехнера, Пирсона, коэффициента ассоциации и т.д.), а в анализе финансово-хозяйственной деятельности чаще используется линейный коэффициент корреляции:

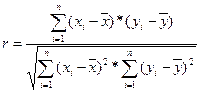или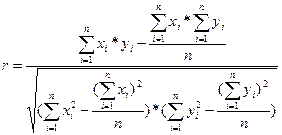

Значение r изменяются в интервале [-1; +1]. r = -1 свидетельствует о наличии жестко детерминированной обратной связи между факторами. r = + 1 – прямая зависимость факторов. r ≈ 0 – связи между факторами не наблюдается. При социально экономическом анализе │r│ < 0,3 – связь слабая: 0,3 <│r│ < 0,7 – связь средней тесноты; │r│ > 0,7 – тесная.

Регрессионный анализ – это метод установления аналитического выражения (модели, уравнения) стохастической зависимости между исследуемыми признаками. В отличие от корреляционного анализа, который отвечает на вопрос, существует ли связь между анализируемыми признаками, регрессионный анализ дает и ее формализованное выражение. В экономических исследованиях корреляционный и регрессионный анализ нередко объединяются в один – корреляционно-регрессионный анализ.

Регрессионная модель может быть построена при наличии любой зависимости (степенной, логарифмической, экспоненциальной и т.д.), однако в многофакторном анализе используют только линейные модели вида:

У = а + b₁x₁ + b₂x₂ +…+ b_m x_m

Коэффициенты рекомендуется определять с помощью аналитических пакетов для персонального компьютера. В наиболее простом случае коэффициенты регрессии однофакторного линейного уравнения регрессии вида у=а+bx можно найти по формулам:

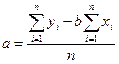
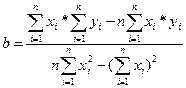
экономический смысл коэффициентов регрессии

Дата добавления: 2014-01-03