Основы корреляционного метода

Лекция № 4

1. Сущность теории корреляции.

2. Вычисление коэффициента корреляции.

3. Оценка точности коэффициента корреляции.

4. Ранговая корреляция.

5. Получение эмпирических формул зависимости явлений.

6. Множественная корреляция.

7. Частная корреляция.

8. Компонентный и факторный анализы.

1 Сущность теории корреляции. Диалектический подход к изучению закономерностей природы и общества требует рассмотрения процессов и явлений в их сложных взаимосвязях.

Явления географической среды зависят от многих, часто неизвест­ных и меняющихся факторов. Выявить и изучить такие связи помогает теория корреляции - один из центральных разделов математической статистики, исключительно важный для исследователей.

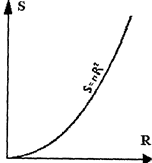
Рисунок 4.1 – Функциональ­ная зависимость

Главные задачи корреляционного анализа - изучение формы, знака (плюс или минус) и тесноты связей.

Опишем кратко сущность теории корреляции.

Все связи делятся на функцио­нальные, рассматриваемые в курсах математического анализа, и корреля­ционные.

Функциональная зависимость предполагает однозначное соответ­ствие между величинами, когда численному значению одной величины, называемой аргументом, соответствует строго определенное значение другой величины - функции. При графическом изображении функцио­нальной связи в прямоугольной системе координат (х, у), если по оси абсцисс отложить значение одного признака, а по оси ординат - друго­го, все точки расположатся на одной линии (прямой или кривой). Функ­циональные (идеальные) связи встречаются в абстрактных математиче­ских обобщениях. Например, зависимость площади круга от радиуса (R) выразится на графике определенной кривой (рис. 1), построенной по формуле

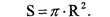
В любой опытной науке экспериментатор имеет дело не с функ­циональными связями, а с корреляционными, для которых характерен известный разброс результатов эксперимента. Причина колеблемости заключается в том, что функция (изучаемое явление) зависит не только от одного или нескольких рассматриваемых факторов, но и от множест­ва других. Так, урожайность зерновых культур будет зависеть от ряда климатических, почвенных, экономических и других условий. Если связь урожайности с каким-либо из указанных факторов изобразить графически в системе координат (х, у), то получим разброс точек. Зако­номерности корреляционных связей и изучает теория корреляции.

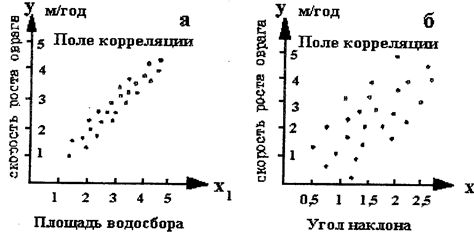
В основе теории корреляции лежит представление о тесноте связи между изучаемыми явлениями (большая или малая связь). Для луч­шего уяснения редко встречаемого в географической литературе поня­тия «теснота связи» представим его в графической форме путем построения так называемого поля корреляции. Для этого результаты каждого наблюдения за элементами статистической совокупности по двум признакам отмечаем точкой в системе прямоугольных координат х и у. Таким путем, например, можно изобразить зависимость урожайно­сти зерновых по районам от гидротермического коэффициента. Чем больше разброс точек на поле корреляции, тем меньше теснота связи между изучаемыми явлениями. Рассмотрим два корреляционных поля (а и б, рис. 4.2). На поле а показана зависимость скорости роста оврагов (у) от площади водосбора (xi), на поле б - от угла наклона (хз). Меньший разброс точек первого корреляционного поля указывает на то, что скорость роста оврагов более тесно связана с площадями водосбо­ров, чем с углами наклона. Иначе можно сказать: изучаемое явление зависит от первого картометрического показателя в большей степени.

По общему направлению роя точек - слева вверх направо - можно заключить, что в обоих случаях связь положительная (со знаком плюс).

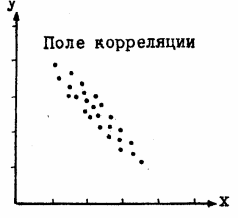Рисунок 4.2 – Корреляционная положительная связь:
а) большая теснота связи б) малая теснота связи

Рисунок 4.3 – Корреляционная отрицательная связь

При отрицательной (минусовой) зависимости рой точек направлен слева вниз направо (рис. 4.3). По характеру размещения точек в рое, их близо­сти к оси можно визуально определить не только тесноту и знак связи, но и ее форму, которая подразделяется на прямолинейную и криволинейную.

Первая форма связи воспроиз­ведена на рис. 4.2 а и б. Она условна и является частным случаем связи криволинейной. Однако именно прямолинейная связь (при всей ее условности) рассматривается в географических и других исследо­ваниях наиболее часто из-за простоты математико-статистического аппарата ее оценки и возможности применения при изучении многофакторных связей и зависимостей.

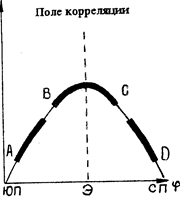
Рисунок 4.4 – Криволинейная форма связи

Степень кривизны географических корреляционных связей во многом зависит от меридиональной протяженности изучаемых терри­торий. На рисунке 4.4 показана в схематизированном виде криволинейная зависимость среднегодовой температуры (t) от географической широты t(j) в глобальном масштабе - от южного полюса (ЮП) через экватор (Э) до северного полюса (СП). Чем меньше протяженность изучаемой территории с юга на север, тем больше оснований назвать ее прямолинейной.

Так, на восходящем отрезке АВ (южное полушарие) связь прямолинейная положительная, а на нисходящем отрезке CD (северное полушарие) - прямолинейная отрицательная. На приэкваториальном отрезке ВС связь сохраняется криволинейной.

Визуально-графический способ изучения тесноты и формы связи прост, нагляден, но недоста­точно точен. Математико-статистическая обработка результатов наблюдений позволяет определить чи­словые значения, характеризующие как форму, так и тесноту связей.

2 Вычисление коэффициента корреляции. Наиболее распространенным показателем тесноты прямолинейной связи двух количественных признаков считается коэффициент корре­ляции (r). Его абсолютное численное значение находится в пределах от О до 1. Чем теснее связь, тем больше абсолютное значение г.

Если r = 0, то связи нет, если он равен ±1, то связь функциональ­ная (точки расположатся строго по линии). Знак «плюс» (+) указывает на прямую (положительную) зависимость, «минус» – на обратную (отрицательную). Предельные значения коэффициента корреляции (r = + 1, 0 и - 1) в практике географических исследований не встречаются; обычно их числовые значения находятся между нулем и положительной или отрицательной единицей.

Рассмотрим наиболее распространенную схему вычисления, опирающуюся на предварительные расчеты средних арифметически, центральных отклонений и средних квадратических отклонений да каждого количественного признака. Предположим, необходимо найти тесноту связи между количеством осадков в июле (х) и урожайностью пшеницы (у). Эти данные вносятся в первые два столбца таблицы 1.

Схема вычисления коэффициента корреляции

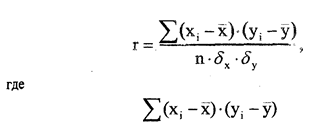
– сумма по столбцу 5; n – число наблюдений; d_x и d _у – средние квадратические отклонения признаков х и у, вычисленные по формуле, при­веденной в лекции 2. В нашем примере связь хорошая.

Таблица 1

X	У	Х-Х	У-У	(х-х).(у-у)	(Х-Х)^2	(У-У)^2
		-50	-10
		-50	-6
		-10	-6
			-1	-10
		-10	-7
					1 600
800 180 0 0 1560 8600 464

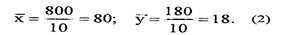
Затем вычисляем разности между конкретными значениями ис­ходных величин и их средними арифметическими. Результаты этих расчетов записываем в столбцы 3 и 4. Вычисление чисел в столбцах 5, б и 7 вполне понятно из надписей над соответствующими столбцами. Под каждым столбцом подсчитываем суммы. Коэффициент корреляции (г) вычисляем по формуле

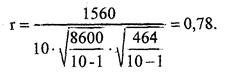
Особо ценен 5-й столбец схемы, представляющий собой совокуп­ность произведений центральных отклонений и названный ковариаци­онным столбцом. Он позволяет проверить правильность определения знака и численного значения коэффициента корреляции по соотноше­нию сумм плюсовых и минусовых показателей членов ковариационного ряда. Чем больше разнятся суммы плюсов и минусов, тем теснее связь исходных показателей. Примерное равенство их свидетельствует о низ­кой связи. Знак коэффициента корреляции будет соответствовать знаку превышения одной суммы над другой.

Коэффициент корреляции, как и d, проще определяется без вы­числения отклонений от средней. Приведем схему такого вычисления по данным предыдущего примера. Схема проста, и для ее понимания достаточно надписей над столбцами таблицы 2.

3 Оценка точности коэффициента корреляции. Как и всякая другая выборочная математико-статистическая ха­рактеристика, коэффициент корреляции имеет свою ошибку репрезен­тативности, вычисляемую при больших выборках (n > 50) по формуле

Таким образом, точность вычисления коэффициента корреляции повышается с увеличением объема выборки; она велика также при большой тесноте связи (r близок к +1 или -1).

Приведем пример вычисления ошибки выборочного r.

Коэффици­ент корреляции между заболеваемостью дизентерией и одним из клима­тических факторов r = 0,82.

Показатель тесноты связи вычисляется по данным 64 пунктов. Тогда

Получив суммы по всем столбцам, вычисляем коэффициент корреляции по формуле

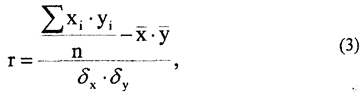
где

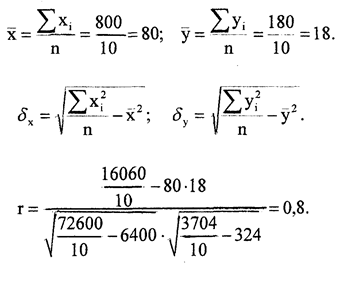
С точностью определения коэффициента корреляции тесно связан вопрос о реальности существования этой связи между рассматриваемы­ми признаками. При малом объеме выборки или малой тесноте связи часто ошибки, коэффициента корреляции оказываются настолько боль­шими и сопоставимыми с самим коэффициентом, что встает вопрос, не случайно ли его значение отличается от нуля и соответствует ли опре­деленный знак связи действительной ее направленности (плюсовой или минусовой?) Этот вопрос разрешается численным сравнением r

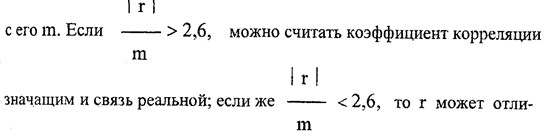
чаться от нуля случайно, и связь явлений не доказывается.

Проверим, существует ли связь между явлениями в нашем примере

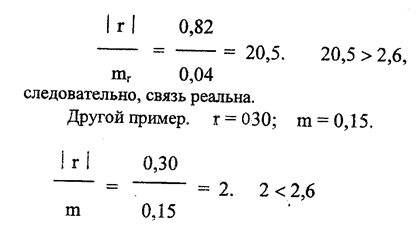
связь недостоверна, то есть ее может и не быть.

4 Ранговая корреляция. В географических исследованиях при малых объемах выбора часто требуется обработать статистический материал быстро, не претендуя на высокую точность. Для этого можно ограничиться вычислением не коэффициента корреляции, а ранговой корреляции. Суть этого показателя состоит в том, что действительные значения количественных признаков заменяются их рангами, то есть последовательным рядом простых чисел, начиная с единицы в порядке возрастания признака Например, имеются данные об урожайности зерновых культур (у) и количестве осадков за два месяца перед колошением (х) по пяти районам (табл. 3, столбцы 1 и 2). Требуется вычислить тесноту связи. Заме­няем значения признаков их рангами Хр и Ур (столбцы 3 и 4), находим разности рангов (столбец 5), затем вычисляем квадраты этих разностей (столбец 6).

Ранговый коэффициент корреляции (r) вычисляется по формуле

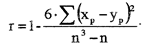
Этот показатель тесноты связи рассчитывается главным образом то­гда, когда достаточно выяснить приближенную величину тесноты связи, и поэтому полученные результаты можно округлять лишь до десятого знака. Ранговый коэффициент корреляции представляет ценность еще и потому, что в распоряжение географа-исследователя часто поступают данные о многих природных и социально-экономических явлениях, заранее выраженные в рангах или баллах, а последние легко перевести в ранги.

5 Получение эмпирических формул зависимости явлений. Корреляционные методы позволяют определить не только тесноту связи явлений, но и эмпирические формулы зависимости, с помощью которых можно по одним признакам находить другие, часто недоступ­ные или мало доступные наблюдению.

При вычислении коэффициента корреляции обычно получают пять основных статистических показателей - 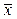, , 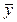d_x , d _у и r. Эти пока­затели дают возможность легко и быстро рассчитать параметры линей­ной зависимости у от х. Известно, что такая зависимость выражается формулой

Параметры а и b вычисляются по формулам

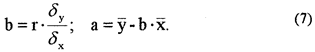
Например, необходимо построить эмпирическую формулу линей­ной зависимости урожайности (у) от процента гумуса в почве (х). При вычислении коэффициента корреляции были получены следующие

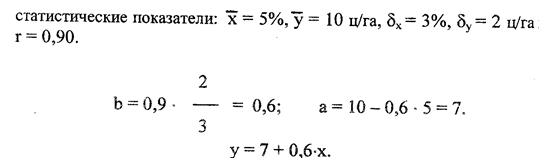
По найденной формуле можно представить примерную урожай­ность, зная процент гумуса на любом участке изучаемой территории. Так, если процент гумуса равен 10, то следует ожидать урожайность у = 7+0,6-х ==7+0,6-10 =13 ц/га.

Чем больше абсолютная величина r, тем более точной и надежной будет эмпирическая формула зависимости.

6 Множественная корреляция. При изучении многофакторных связей встает проблема определе­ния степени совместного влияния нескольких факторов на исследуемое явление.

Корреляционный анализ обычно начинается с вычисления парных коэффициентов корреляции (r_xy), выражающих степень зависимости изучаемого явления (у) от какого-либо фактора (х). Например, опреде­ляются коэффициенты корреляции между урожайностью зерновых культур, с одной стороны, и рядом климатических, почвенных и эконо­мических факторов — с другой. Анализ полученных парных коэффициентов корреляции позволяет выявить наиболее важные факторы уро­жайности.

Следующая ступень корреляционного анализа заключается в том, что вычисляется коэффициент множественной корреляции (R), показы­вающий степень совместного влияния важнейших факторов (x₁, x₂,... x_n) на изучаемое явление (у), например, на урожайность зерновых куль­тур. Расчет для множества факторов представляет собой очень трудоем­кий процесс, часто требующий применения ЭВМ.

Рассмотрим простейший пример вычисления степени совокупного влияния на урожайность (у) только двух факторов: гидротермического коэффициента (x₁) и стоимости основных средств производства (х₂). Для этого вначале следует определить коэффициенты корреляции меж­ду тремя признаками (у, x₁, и х₂) попарно. Оказалось, что

1) коэффициент корреляции между урожайностью зерновых культур (у) и гидротермическим коэффициентом (х₁) 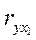== 0,80;

2) коэффициент корреляции между урожайностью зерновых культур (у) и стоимостью основных средств производства (х₂) 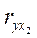== 0,67;

3) коэффициент корреляции между самими факторами урожайности (гидротермическим коэффициентом и стоимостью основных средств производства) 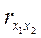= 0,31.

Коэффициент множественной корреляции, выражающий зависи­мость изучаемого явления от совокупного влияния двух факторов, вы­числяется по формуле

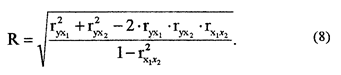
В нашем примере

Совокупное влияние нескольких факторов на изучаемое явление больше, чем каждого из этих факторов в отдельности. Действительно, 0,92 больше как 0,80, так и 0,67.

Квадрат коэффициента множественной корреляции (R² = 0,84) означает, что колеблемость урожайности зерновых объясняется воздей­ствием учтенных факторов (гидротермические коэффициенты и стои­мость основных средств производства) на 84%. На долю остальных неучтенных факторов приходится всего 16%.

Линейную зависимость одной переменной (у) от двух других можно выразить уравнением

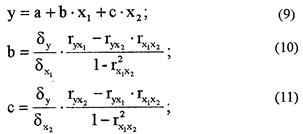
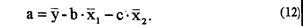
7 Частная корреляция. В предыдущем параграфе была рассмотрена схема вычисления я коэффициента множественной корреляции, выражающего степень совместного воздействия двух факторов (x₁ и х₂) на изучаемое явление у. Представляет интерес выявить, как тесно связан у с x₁ при постоянстве величине х₂; или у с х₂ при исключении влияния x₁. Для этого следу вычислить коэффициент частной корреляции (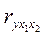) по формуле:

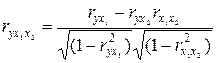, (13)

Где ryx₁ – коэффициент корреляции между первым фактором и изучаемым явлением (у), ryx₂ – коэффициент корреляции между вторым фактором (х₂) и изучаемым явлением (у), rx₁x₂ – коэффициент корреляции между факторами (х₁) (х₂)

Пользу коэффициента частной корреляции покажем на приме изучения овражной эрозии. Известно, что скорость роста оврагов во многом зависит от энергии поверхностного стока, определяемой eё объемом и скоростью. Первая характеристика может быть выражена таким морфометрическим показателем, как площадь водосбора при вершине оврага, а скорость стока - углом наклона у вершины оврага. Были измерены скорости роста n-го числа оврагов (у), углы наклов (x₁) и площади водосбора (х₂), вычислены парные коэффициенты корреляции: 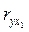=: - 0,2, 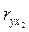= 0,8; 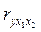== - 0,7. Отрицательное значение первого коэффициента корреляции выглядит парадоксальным. Действительно, трудно представить, чтобы скорости роста оврагов были тем больше, чем меньше угол наклона.

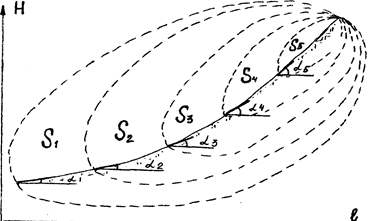
Рисунок 4.5 – Продольный профиль балки растущего оврага

Объяснить эту аномалию может обычно вогнутая форма продольного профиля балки, где растет овраг (рис. 4.5). Благодаря такой форме профиля наблюдается противоположность воздействия двух рассматриваемых факторов (x₁, и х₂) на ско­рость роста оврагов (у): овраг, начинающий свое развитие в устье балка имеет малый угол наклона (a_i), но зато наибольшую площадь водосбо­ра, обеспечивающую максимальный объем стекающей воды. По мера приближения вершины оврага к водоразделу угол наклона растет (a₁, a₂, a₃, a₄, a₅), но площадь водосбора уменьшается (S₁ – S₅). Преоб­ладающее воздействие площади водосбора (объема воды) над воздейст­вием угла наклона (ее скорости) и привело к отрицательному значению зависимости скорости роста оврагов от угла наклона. Разнонаправленность воздействия двух рассмотренных факторов объясняет также ми­нусовой знак их корреляционной взаимозависимости (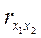== - 0.7). Для того, чтобы определить, насколько велика зависимость скорости роста оврагов от угла наклона при исключении влияния другого фактора (площади водосбора), необходимо вычислить коэффициент частной корреляции по формуле (13). Оказалось, что

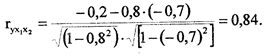
Таким образом, только в результате корреляционных расчетов ста­ло возможным убедиться в прямой, а не обратной зависимости скорости роста оврагов от угла наклона, но только при условии исключения воз­действия площади водосбора.

8 Компонентный и факторный анализы. Из множества известных показателей тесноты корреляционных связей следует подчеркнуть особо важное значение коэффициента кор­реляции. Его отличает прежде всего повышенная информативность -способность оценивать не только тесноту, но и знак связи. Коэффици­енты корреляции лежат в основе вычисления более сложных показате­лей, характеризующих взаимосвязи не двух, а большего числа факторов.

Рассмотренный в настоящей лекции аппарат множественной и ча­стной корреляции правомерно считать начальным этапом изучения многофакторных корреляционных связей и зависимостей в географии. В условиях активной информатизации и компьютеризации человеческо­го общества наших дней перспектива развития этого направления ви­дится в использовании более сложного аппарата факторного и компо­нентного анализов. Их объединяет: наличие исключительно большого объема разнообразной информации, необходимость ее математической обработки с помощью ЭВМ, способность «сжимать» информацию, выделять главные и исключать второстепенные показатели, факторы и компоненты.

Факторный анализ предназначен для сведения множества исходныx количественных показателей к малому числу факторов. На их основе вычисляются интегральные показатели, несущие в себе информацию нового качества. В основе математических расчетов лежит создание матрицы, элементами которой выступают обычные коэффициенты корреляции или ковариации, отражающие попарные связи между всеми исходными количественными показателями.

Компонентный анализ (метод главных компонент) в отличие о факторного анализа опирается на массовые расчеты не корреляций, дисперсий, характеризующих колеблемость количественных признаке; л

В результате таких математических расчетов любое самое большое число исходных данных заменяется ограниченным числом главных компонент, отличающихся наиболее высокой дисперсностью, а, следовательно, и информативностью.

Желающим глубже познакомиться с теорией, методикой и накопленным опытом использования факторного и компонентного анализов в географических исследованиях следует обратиться к работам С.Н. Сербенюка (1972), Г.Т. Максимова (1972), П.И. Рахлина (1973), В.Т. Жукова, С.Н. Сербенюка, B.C. Тикунова (1980), В.М. Жуковской (1964), B.M. Жуковской, И.М. Кузиной (1973), В.М. Жуковской, И.Б. Мучник (1976):

В заключение отметим, что при криволинейных зависимостях коэффициенту корреляции не всегда можно доверять, особенно когда изучаются природные явления на территориях значительной протяжен­ности с севера на юг. В этом случае лучше вычислять корреляционные отношения, которые нуждаются в большом объеме статистической со­вокупности и в предварительной группировке данных (Лукомский, 1961).

ВОПРОСЫ И ЗАДАНИЯ

1. Назовите главные задачи корреляционного анализа.

2. Опишите схему вычисления коэффициента корреляции.

3. Как вычисляется ошибка выборочного коэффициента корреляции?

4. Какова схема вычисления рангового коэффициента корреляции?

5. Опишите получение эмпирических формул зависимости для двух показателей. Каково их использование?

6. В чем сущность множественного коэффициента корреляции?

7. Каково назначение частного коэффициента корреляции?

8. Что такое компонентный анализ?

9. Дайте определение факторного анализа.

Дата добавления: 2014-01-03