Целевая функция 1 страница

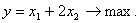
Ограничения:

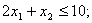
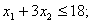
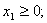
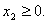
1 этап. Построение области допустимых решений (ОДР).

Для формирования ОДР необходимо в системе координат 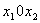построить линии, соответствующие ограничениям, приравнивая их левые и правые части, и определить направления расположения допустимых значений искомых переменных в соответствии со знаками неравенств (рис.6.1).

Рис.6.1. Графическая иллюстрация решения задачи линейного программирования

Вычисления для построения первых двух ограничений:

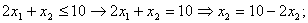
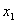
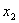
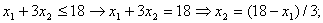
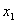
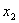
Направления допустимости значений переменных 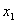и 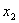в соответствии с первыми двумя ограничениями – «вниз - влево». В соответствии с третьим ограничением значения переменной 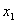должны находиться выше оси 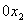, а в соответствии с четвертым ограничением значения переменной 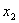должны находиться правее оси 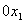. Следует иметь в виду, что границы ОДР в область допустимых решений входят. Это объясняется тем, что в ограничениях применяются знаки неравенств «меньше – равно» и «больше – равно».

2 этап. Окончательное определение оптимальных значений переменных 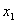и .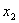

Для этого необходимо сначала построить произвольную прямую для целевой функции, приравняв ее выражение к любому числу, так, чтобы эта прямая располагалась в пределах выбранного масштаба рисунка. Приравняем выражение целевой функции, например, к числу «16» и построим соответствующую прямую линию.

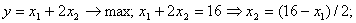
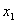
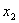
После этого необходимо построить прямую линию, параллельную данной прямой, так, чтобы она коснулась границы ОДР. Координаты точки касания этой прямой с границей ОДР будут оптимальными значениями переменных 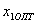и .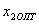

Для точного определения координат точки касания линии целевой функции границы ОДР (точных значени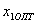й и 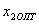) необходимо решить систему, включающую в себя два уравнения: 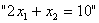и 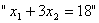. Решим эту систему уравнений: 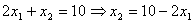. Подставим это значение 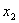во второе уравнение:

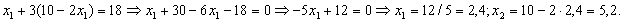
Т.е.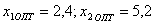. При этом максимальное значение целевой функции .

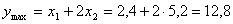Симплекс метод решения задач линейного программирования

ОДР в двухпараметрической задаче линейного программирования представляет собой плоский многогранник (см. предыдущий пример), а в общем виде это выпуклый многогранник.

Теорема: экстремум целевой функции в задаче линейного программирования, если он существует, всегда является абсолютным и достигается хотя бы в одной крайней точке многогранника, определяющего ОДР.

Примечание. Крайние точки – это точки пересечения границ ОДР.

Идея симплекс метода заключается в направленном переборе крайних точек ОДР. Этот метод является классическим в линейном программировании.

Пример. Требуется минимизировать целевую функцию

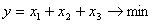
при следующих ограничениях:

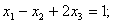
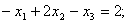
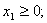
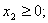
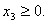
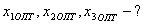
Поcтавим в соответствие этой задаче следующую систему линейных уравнений:

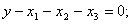
(6.1)

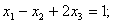
(6.2)

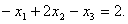
(6.3)

Решим эту систему методом последовательного исключения неизвестных (методом Гаусса). В его основе лежат следующие элементарные преобразования:

1. Умножение какого - либо уравнения на число, отличное от нуля;

2. Сложение двух уравнений и последующая замена одного из них получившейся суммой;

3. Перемена местами любых двух уравнений.

С помощью элементарных преобразований получим следующую систему:

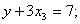
(6.4)

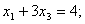
(6.5)

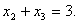
(6.6)

Уравнение (6.6) – это сумма уравнений (6.2) и (6.3).

Уравнение (6.5) – это сумма уравнений (6.2) и (6.6).

Уравнение (6.4) - это сумма уравнения (6.1) и уравнений (6.5) и (6.6).

Пусть 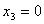, при этом значения переменных будут следующими: .

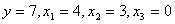Эти значения являются решением системы уравнений (6.4) – (6.6) и, значит, системы уравнений (6.1) – (6.3). Причем, 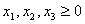, т.е. найденное решение допустимо.

Т.к.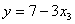 (см.6.4), то для уменьшения значения целевой функции необходимо увеличить 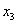, но увеличивать его бесконечно нельзя, иначе величины 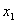и 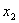станут отрицательными (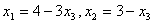, эти выражения получены соответственно из уравнений 6.5 и 6.6). Согласно первому уравнению 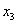может быть равным 4/3, согласно второму уравнению 3. Для того, чтобы все условия задачи выполнялись, необходимо взять наименьшее из этих значений - 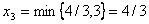(если принять 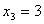,то 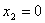, что приемлемо, а 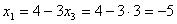, что не приемлемо для нашей задачи, т.е. необходимо принять 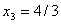). Тогда из уравнения (6.5) следует, что .

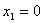С помощью элементарных преобразований приведем систему уравнений (6.4) – (6.6) к следующей системе:

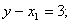
(6.7)

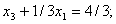
(6.8)

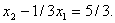
(6.9)

Система (6.7) – (6.9) из системы (6.4) – (6.6) получена следующим образом:

,

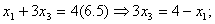
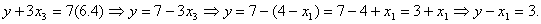
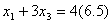разделим это уравнение на 3, получим 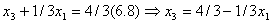- подставим в (6.6)

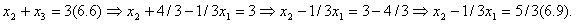
Запишем решение системы уравнений (6.7) – (6.9):

.

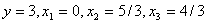Здесь 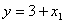, уменьшать 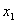для дальнейшего уменьшения целевой функции нельзя, т.к. оно станет отрицательным, увеличивать его нет смысла, т.к. при этом увеличивается целевая функция. Следовательно, полученное значение 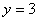является минимальным, и ему соответствует оптимальные значения искомых переменных: 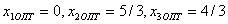. Эти оптимальные значения переменных справедливы и для исходной задачи.

Симплекс – метод. Этапы поиска решений

Для использования симплекс - метода, задачу линейного программирования необходимо привести к стандартному виду: найти 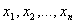, доставляющие минимум целевой функции

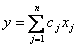
при условиях:

…

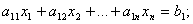
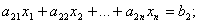
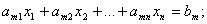
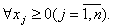
Здесь значок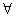означает «все».

C формальной точки зрения нет необходимости строго различать задачи поиска минимума или максимума целевой функции. Одна задача сводится к другой изменением знака 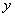на противоположный. Все 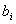должны быть положительными, в противном случае соответствующее уравнение умножается на (-1).

Рассмотрим этапы поиска решений симплекс – методом на следующем примере.

Пример. Модель раскроя листовых материалов. Выбор наилучшего варианта.

Имеется некоторый материал в виде стандартных листов, которые необходимо раскроить для получения не менее 80шт. деталей типа 1 и не менее 40шт. деталей типа 2. Известны четыре способа раскроя листа, каждый из которых дает результат, представленный в таблице 6.1.

Таблица 6.1 Исходные данные для решения задачи

Способы раскроя листа
Результат	3 детали типа 1; 1 деталь типа 2	2 детали типа 1; 6 деталей типа 2	1 деталь типа 1; 9 деталей типа 2	0 деталей типа 1; 13 деталей типа 2

Требуется так провести операцию изготовления деталей, чтобы общий расход листов оказался минимальным.

Пусть 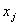– количество листов, раскраиваемых j – м способом (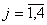). Тогда целевая функция, будет иметь следующий вид:

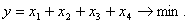
Здесь 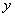– это общий суммарный расход листов.

Формулировка задачи. Найти 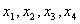, доставляющие минимум приведенной выше целевой функции при следующих ограничениях:

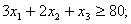
(6.10)

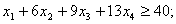
(6.11)

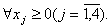
(6.12)

Ограничение (6.10) обеспечивает заданное число деталей типа 1, ограничение (6.11) – заданное число деталей типа 2. Ограничение (6.12) необходимо, т.к. количество листов не может быть отрицательным.

Для того, чтобы для решения данной задачи применить симплекс метод, необходимо систему (6.10) – (6.12) привести к стандартному виду:

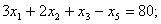
(6.13)

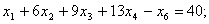
(6.14)

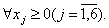
(6.15)

Очевидно следующее решение системы (6.13) – (6.15): .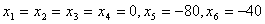

Это решение называется базисным. Оно неприемлемо, т.к. 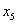и 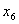отрицательны. Следовательно, систему (6.13) – (6.15) необходимо преобразовать и решать ее в два этапа.

1 этап. Вспомогательный.

Он выполняется для нахождения приемлемого (допустимого) и оптимального для данного этапа базисного решения, т.е. по существу координат одной крайней точки области допустимых решений с целью направленного перебора на втором этапе остальных крайних точек для выбора оптимального решения для задачи в целом.

Преобразуем систему (6.13) – (6.15) в систему (6.16) – (6.18):

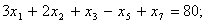
(6.16)

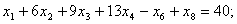
(6.17)

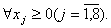
(6.18)

Ставим вспомогательную задачу. Необходимо найти 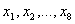, доставляющие минимум следующей целевой функции: 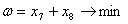. Здесь легко находятся исходное допустимое базисное решение:

.

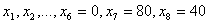После этого начинается реализация симплекс – алгоритма для решения вспомогательной задачи. Работа при этом осуществляется c системой (6.16) – (6.18).

1. Выражаются базисные переменные 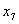и 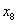через свободные переменные

.

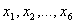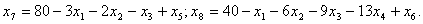
2. Определяется целевая функция:

.

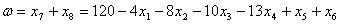3. Анализируется выражение для целевой функции, в нем присутствуют отрицательные коэффициенты, значит текущее базисное решение не оптимально.

Теорема. Допустимое базисное решение является оптимальным, если коэффициенты 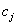при свободных переменных 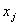в выражении для целевой функции неотрицательны.

Для текущего базисного решения 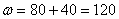, т.к. .

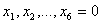4. В выражении для целевой функции находится переменная, имеющая наибольший по модулю отрицательный коэффициент, она вводится в базис для получения нового базисного решения.

Для этого анализируются зависимости текущих базисных переменных (здесь 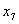и 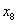), от вводимой в базис переменной (здесь 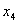, т.к. она имеет коэффициент «-13») при условии, что свободные переменные равны нулю (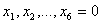): 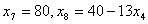. Очевидно, что 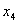можно увеличить самое большее до 40/13, при этом

,

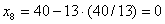т.е. получим новое базисное решение:

.

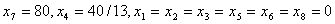Снова выполняем симплекс алгоритм:

1. Опять выражаем базисные переменные через свободные:

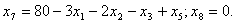
2. .

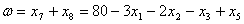3. Минимум 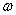не достигнут (текущее базисное решение не оптимально), т.к. выражение для целевой функции содержит переменные с отрицательными коэффициентами. 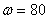, т.к 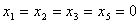, т.е. значение целевой функции уменьшилось по сравнению с предыдущим.

4. Вводим в базис 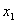, т.к. эта переменная в выражении для целевой функции имеет коэффициент «-3». 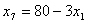, т.к.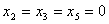. 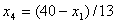, т.к. 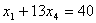(см. уравнение (6.17), принимая во внимание, что 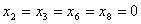). Здесь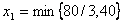,т.е. 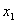можно увеличить до 80/3 (до 40 нельзя, т.к. при этом 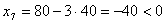). Следовательно, 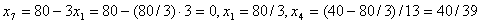, т.е. получили новое базисное решение: .

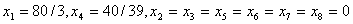Это базисное решение на данном этапе является оптимальным (выражение для целевой функции 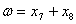не содержит отрицательных коэффициентов). При этом

.

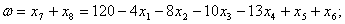
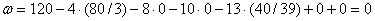Целевую функцию уменьшить нельзя, т.к. .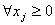

Переменные 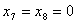, т.е. они перешли в разряд свободных переменных и могут быть отброшены. Окончательное базисное решение 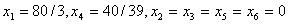является оптимальным для вспомогательного этапа 1 и допустимым для системы (6.13) – (6.15).

2 этап. Работаем с системой (6.13) – (6.15). Имея допустимое базисное решение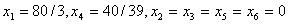, полученное в результате минимизации 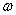на этапе 1, оценим его для исходной задачи с целевой функцией 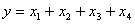. Тем самым начинается повторное использование симплекс - алгоритма, но уже для исходной задачи.

1. С помощью системы (6.13) – (6.15) получим:

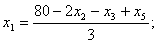
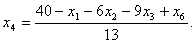
2. 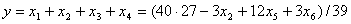(приводится без вывода).

3. Данное базисное решение не оптимально, т.к. переменная 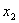имеет отрицательный коэффициент.

4.. Вводим в базис переменную x₂.

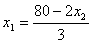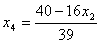; (выражение для 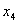приводится без вывода).

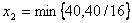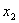, можно увеличить самое большее до 40/16=5/2, при этом

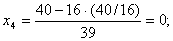
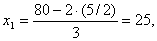
т.е. получили новое базисное решение: .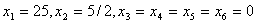

Снова выполняем симплекс – алгоритм:

1,2. Выражаем 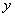через свободные переменные .

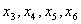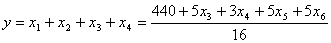(приводится без вывода).

3. В выражении для целевой функции все коэффициенты при переменных положительны. Т.е. текущее базисное решение является оптимальным, значит 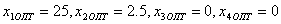. Т.е. наилучший вариант технологии состоит в применении только первого и второго способов раскроя листов, причем первым способом необходимо раскроить 25 листов, а вторым 2,5 листа, тогда наименьший общий суммарный расход листов составит 27,5 шт. Количество получаемых деталей при этом будет: деталь типа 1 –

,

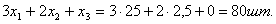деталь типа 2 –

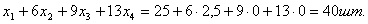
Лекция 7

Численные методы решения задач нелинейного программирования (поиск экстремума функции одной переменной)

Напомним, что задача математического программирования формулируется следующим образом: найти значения переменных 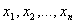, доставляющие максимум или минимум целевой функции 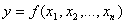при условиях .

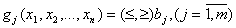Особенность задач нелинейного программирования заключается в том, что функции 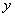и (или) не линейны. Разработано множество численных методов решения задач нелинейного программирования.

Классификация численных методов решения задач нелинейного программирования

1. Численные методы поиска экстремума функции одной переменной.

1.1. Классический метод.

1.2. Метод равномерного перебора.

1.3. Метод золотого сечения.

1.4. Метод Фибоначчи и т.д.

2. Численные методы поиска экстремума функции n – переменных.

2.1. Численные методы в задачах без ограничений.

2.1.1. Метод покоординатного спуска.

2.1.2. Метод Хука – Дживса.

2.1.3. Градиентный метод.

2.1.4. Метод Ньютона.

2.1.5. Метод сопряженных направлений и т.д.

2.2. Численные методы в задачах с ограничениями.

2.2.1. Метод покоординатного спуска.

2.2.2. Метод условного градиента.

2.2.3. Метод барьерных функций.

2.2.4. Метод штрафных функций.

2.2.5. Метод линеаризации и т.д.

Универсального метода, с помощью которого можно было бы решить любую задачу оптимизации, не существует. Поэтому для решения конкретной задачи применяют один или несколько своих численных методов.

Методы поиска экстремума функции одной переменной

Эти методы применяются в однопараметрических задачах оптимизации. В них ищется один оптимальный параметр. Целевая функция – это функция одной переменной.

Постановка задачи. Найти значение переменной 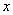, доставляющее минимум или максимум целевой функции 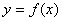, при условиях .

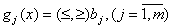Классический метод минимизации (максимизации) функции одной переменной

Пусть 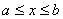, функция 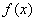непрерывна на этом отрезке и имеет на нем непрерывную производную. Вычисляют значение производной 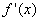и определяют критические точки, т.е. такие внутренние точки отрезка 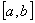, в которых производная обращается в нуль или не существует. В окрестности каждой такой критической точки исследуют знак производной и отбирают те из них, при переходе через которые производная меняет знак с минуса на плюс (это точки локального минимума) или с плюса на минус (это точки локального максимума). Затем вычисляют значения целевой функции в этих точках и на границах отрезка 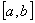. Эти значения сравнивают между собой и определяют точку, в которой достигается минимум (максимум) целевой функции. Эта точка является точкой глобального минимума (максимума) функции 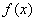на отрезке .

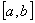Дата добавления: 2014-01-03