Целевая функция 3 страница

Недостатки:

1. Трудности (субъективизм) в определении весовых коэффициентов.

2. Аддитивный критерий не вытекает из объектной роли частных критериев и поэтому выступает как формальный математический прием.

3. В аддитивном критерии происходит взаимная компенсация частных критериев, т.е. уменьшение одного из них может быть компенсировано увеличением другого критерия.

Мультипликативный критерий

Целевая функция здесь записывается следующим образом:

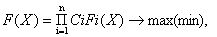
где П – знак произведения;

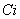- весовой коэффициент i -го частного критерия;

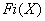- числовое значение i -го частного критерия.

Преимущества мультипликативного критерия:

1. Не требуется нормирование частных критериев.

2. Практически всегда определяется одно оптимальное решение.

Недостатки:

1. Трудности (субъективизм) в определении весовых коэффициентов.

2. Перемножение разных размерностей.

3. Взаимная компенсация значений частных критериев.

Максиминный (минимаксный) критерий

Эти критерии работают по принципу компромисса, который основывается на идее равномерности. Сущность принципа максимина заключается в следующем. При проектировании сложных систем, при наличии большого числа частных критериев установить между ними аналитическую взаимосвязь очень сложно. Поэтому стараются найти такие значения переменных (параметров) 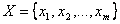, при которых нормированные значения всех частных критериев равны между собой:

где 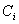- весовой коэффициент i -го частного критерия;

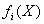– нормированное значение i -го частного критерия;

K – константа.

При большом количестве частных критериев из-за сложных взаимосвязей добиться выполнения указанного выше соотношения очень сложно. Поэтому на практике так варьируют значениями переменных проектирования x ₁, x ₂, …, x _m, при которых последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Т.к. эта операция производится в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравновешивания противоречивых частных критериев, что и является целью принципа максимина.

Формально принцип максимина формулируется следующим образом: выбрать такой набор переменных 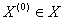, при котором реализуется максимум из минимальных нормированных значений частных критериев, т.е. .

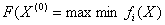Такой принцип выбора 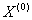иногда носит название гарантированного результата. Он заимствован из теории игр, где является основным принципом.

Если частные критерии необходимо минимизировать, то самым отстающим критерием является тот, который принимает максимальное значение. В этом случае применяют принцип минимакса:

.

Основные принципы выбора критериев оптимальности

Выбор критериев – сложная задача, т.к. цели при проектировании любого объекта, как правило, противоречивы (обеспечение минимальной стоимости и максимальной надежности, максимальной производительности и минимальной энергоемкости и т.д.).

Если требуется оптимизировать один из показателей качества проектируемого объекта при соблюдении ограничительных требований на остальные показатели, то нужно сформировать один частный критерий. Задача оптимизации при этом сводится к задаче максимизации (минимизации) данного критерия с учетом заданных ограничений.

При наличии нескольких критериев выбирают:

а) аддитивный критерий, если существенное значение имеют абсолютные значения критериев при выбранном векторе параметров X;

б) мультипликативный критерий, если существенную роль играет изменение абсолютных значений частных критериев при вариации вектора X;

в) максиминный (минимаксный) критерий, если стоит задача достижения равенства нормированных значений противоречивых (конфликтных) частных критериев.

Лекция 10

Математическое моделирование силового взаимодействия в зоне резания при изготовлении деталей на станках

Данная лекция открывает цикл лекций, посвященный математическому моделированию физических процессов в технологических системах.

Методы расчета сил резания при обработке деталей на металлорежущих станках рассматриваются в курсе «Резание металлов». Здесь в начале лекции мы лишь вспомним некоторые известные силовые зависимости. Итак, например, для расчета сил резания при точении используются следующие формулы:

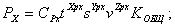
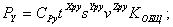
где – соответственно, осевая, радиальная и тангенциальная составляющие силы резания

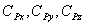– константы (удельные силы резания), учитывающие влияние на силы резания всех прочих параметров, не входящих в формулы (геометрии инструмента, вида обрабатываемого материала, смазочно - охлаждающей технологической среды (СОТС) и т.д.);

t, s, v - глубина, подача и скорость резания;

x, y, z - показатели степени, выражающие влияние соответствующего параметра режима резания на силы резания;

K_ОБЩ - коэффициент, учитывающий дополнительно влияние на силы резания свойств обрабатываемого, инструментального материала и т.д.

При сверлении для определения силовых параметров используются следующие формулы:

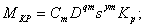
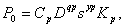
где M_{КР ,} P₀ – соответственно, крутящий момент и осевая сила резания;

C_m, C_p - константы, зависящие от свойств обрабатываемого материала и вида обработки;

D - диаметр обрабатываемого отверстия;

s - подача;

q, y - показатели степени, определяющие степень влияния соответствующего параметра на крутящий момент или осевую силу резания;

K_p - коэффициент, зависящий от свойств обрабатываемого материала.

Эти формулы (математические модели) используются для практических расчетов. Они получены эмпирическим путем, т.е. на основании проведения экспериментов и обработки их результатов. Имеются и теоретически полученные уравнения, но они сложны и для практических расчетов не используются. Наша дальнейшая задача в данной лекции освоить порядок проведения силовых экспериментов и обработки их результатов с целью получения математических моделей.

Порядок проведения силовых экспериментов и аппроксимации результатов измерений (получения математических моделей)

В качестве измерительных приборов при проведении силовых экспериментов для измерения сил резания используются динамометры. Их схемы и принципы работы приведены в специальной литературе и рассматриваются в соответствующих разделах курса «Резание металлов».

При установлении силовых зависимостей, как правило, проводят однофакторные эксперименты. В ходе таких экспериментов варьируют только тем параметром (фактором), влияние которого изучают, а все остальные факторы за время опыта остаются постоянными. Например, устанавливают влияние подачи на силу резания. Принимают разные значения подачи и измеряют соответствующее им значения силы резания. Все остальные параметры, а именно, обрабатываемый и инструментальный материалы, геометрические параметры резца, вид СОТС, глубину, скорость и т.д. оставляют неизменными.

Конечная цель эксперимента - установление функциональной связи (зависимости) между варьируемым параметром и силой резания и описание этой зависимости математической формулой. После установления всех частных зависимостей получают общую зависимость способом, приведенным ниже.

Каждый эксперимент состоит из ряда опытов. В каждом опыте принимаются разные значения исследуемого параметра. Для обеспечения требуемой точности эксперимента в каждом опыте проводится определенное количество повторений или дублей. Например, для обеспечения уровня надежности (доверительной вероятности) 0,9 количество дублей в каждом опыте должно быть не менее 5. Для обеспечения уровня надежности (доверительной вероятности) 0,95 количество повторений должно быть не менее 7.

Прежде чем математически обработать полученные экспериментальные данные значения силы, полученные в каждом опыте, усредняют. Обозначим значение силы через «y», а значение исследуемого параметра через «x». Т.е., например, «y» - это P_X,или P_Y,или P_Z, а «x» - s,или t, или v. Среднее значение силы в каждом опыте y определится следующим образом:

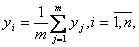
где i – номер текущего опыта;

m – количество повторений в i – ом опыте;

j – номер текущего дубля или повторения;

y_j – значение силы в j – м дубле;

n – количество опытов в эксперименте.

После этого все данные сводятся в таблицу:

Номер опыта			…..	n
x	x1	x2	…..	xn
y	y1	y2	…..	yn

Полученные экспериментальные данные для получения формул подвергают следующей обработке. Сначала выбирают формулу для описания будущей зависимости. Важно правильно выбрать вид аппроксимирующей формулы («аппроксимация» - упрощение в том смысле, что зависимость между функцией «y» и аргументом «x» воплощена и в виде приведенной выше таблицы, но эта зависимость более просто будет описана в виде аппроксимирующей формулы).

Основные требования к аппроксимирующей формуле:

1. Максимальная точность описания устанавливаемой зависимости.

2. Простота

3. Обеспечение быстроты обработки экспериментальных данных.

Многолетние наблюдения показали, что зависимость силы резания от параметров резания хорошо описываются аппроксимирующей функцией вида:

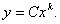
Задача состоит в том, чтобы определить неизвестные коэффициенты C и k. Для упрощения вычислений эту степенную зависимость логарифмируют:

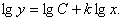
В логарифмических координатах эта функция изображается прямой линией – рис. 10.1.

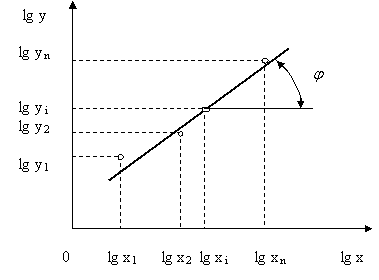
Рис.10.1. Аппроксимация экспериментальных данных в логарифмических координатах

Через опытные точки проводят прямую линию так, чтобы возможно большее число точек равномерно группировалось вокруг нее. Тогда 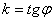(тангенсу угла наклона прямой к оси абcцисс). Далее берется опытная точка на прямой, и определяется постоянная C: 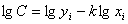. После потенцирования находится явное значение постоянной C.

Приведенный способ применяют, тогда когда зависимость y = f (x) монотонна и экспериментальные точки плотно группируются вокруг прямой. Только в этом случае возможно обеспечить требуемую точность. Если приведенные выше условия не выполняются, то для обработки экспериментальных данных применяют метод наименьших квадратов (метод Гаусса). Для его использования применяют исходную формулу или ее опять логарифмируют. В последнем случае после логарифмирования проще решать уравнения. В настоящее время при реализации метода наименьших квадратов на компьютере надобность в логарифмировании исходной формулы практически отпала.

Аналитическая обработка экспериментальных данных методом наименьших квадратов

Для понимания сути данного метода рассмотрим сначала рис.10.2. На нем в обычных и логарифмических координатах изображены опытные значения (точки) и, соответственно, аппроксимирующая кривая и аппроксимирующая прямая.

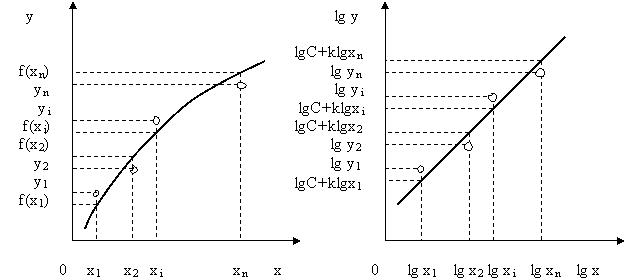
Рис.10.2. Иллюстрация реализации метода наименьших квадратов

На данном рисунке y ₁, y ₂, …, y _n – экспериментальные значения, f (x ₁), f (x ₂), …, f (x _n) – расчетные значения аппроксимирующей функции. Аналогичные значения, но только в логарифмическом измерении, приведены на правой части рисунка.

В основе метода наименьших квадратов лежит следующее положение: наилучшее приближение аппроксимирующей функции y = f (x) к экспериментальным данным будет в том случае, когда сумма квадратов отклонений расчетных значений f (x ₁), f (x ₂), …, f (x _n) от экспериментальных данных y ₁, y ₂ … y _n, является минимальной, т.е.

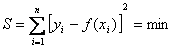
или

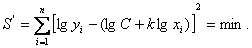
Разность 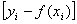в выражении для S есть отклонение по ординате i – ой экспериментальной точки от заменяющей (аппроксимирующей) кривой. Квадраты отклонений берутся, чтобы компенсировать знаки «-» отклонений.

Сумма S^’ будет минимальной, если ее частные производные по параметрам C и k равны нулю. Произведя дифференцирование и соответствующие преобразования, получают систему нормальных уравнений, которая затем решается для нахождения искомой постоянной C и показателя степени k. Существуют компьютерные программы для обработки экспериментальных данных с целью получения аппроксимирующих функций, реализующие метод наименьших квадратов.

Выражение 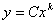является математической моделью объекта исследования (здесь процесса резания). Поэтому после получения численных значений C и k необходимо проверить степень соответствия (адекватность) принятой математической модели описываемому объекту. Проверку адекватности производят, например, по F-критерию Фишера. Если принятая аппроксимирующая функция не удовлетворяет критерию Фишера, то она должна быть заменена другой.

После получения частных зависимостей их объединяют в общую зависимость. Пример объединения двух частных зависимостей. Пусть в результате проведения двух серий экспериментов получены следующие зависимости:

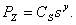
Обе серии экспериментов проводились при неизменных обрабатываемом и инструментальном материалах, скорости резания, СОТС и т.д. Кроме этого первая серия экспериментов была выполнена при постоянной подаче s = s const, а вторая при постоянной глубине резания t = t const. Общая формула, выражающая одновременно влияние t и s на силу P_Z, имеет вид:

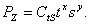
Здесь неизвестна постоянная , которая описывает влияние на силу P_Z всех факторов процесса резания, остававшихся постоянными при проведении обеих серий экспериментов, т.е. всех факторов, кроме подачи и глубины резания. Общая формула превращается в частные, если в нее подставить соответственно или 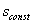, при которой проводилась первая серия экспериментов, или 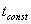, при которой проводилась вторая серия экспериментов:

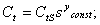
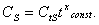
Используя данные первой и второй серии опытов, получим:

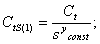
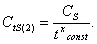
Вследствие неизбежных погрешностей экспериментов величины , полученные из первой и второй серии опытов, будут отличаться друг от друга. Поэтому окончательно принимают:

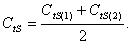
Подобным же образом объединяют три и более частных зависимости.

Полученные формулы не являются физическими законами. Они получены на основе обработки вполне реальных экспериментальных данных, поэтому имеют определенную область адекватности. Т.е. за пределами этой области их использовать нельзя. Например, если силовая зависимость была получена для подач от 0,1мм/об до 0,5 мм/об, то при подачах меньше 0,1 или больше 0,5 мм/об эту формулу использовать нельзя. Всякая экстраполяция за пределами области адекватности может привести к существенным ошибкам в расчетах.

Лекция 11

Математическое моделирование упругих деформаций в технологической системе

При обработке деталей на металлорежущих станках сам станок, приспособление, инструмент и элементы его крепления, обрабатываемая заготовка представляют собой упругую систему, которая называется упругой системой СПИД.

При обработке сила резания изменяется под действием переменных условий обработки, а именно неравномерности глубины резания, колебания твердости обрабатываемого материала и т.д. Колебания силы резания приводят к упругим деформациям деталей системы СПИД и смещению этих деталей по отношению друг к другу за счет наличия зазоров в соединениях. Кроме этого упругая система СПИД обладает не бесконечной жесткостью, причем эта жесткость также является случайной величиной, т.е. может изменять свое значение от наименьшего до наибольшего. Все это вместе взятое оказывает влияние на формирование точности обработки.

Формирование упругих перемещений и смещения элементов в технологической системе и влияния их на точность обработки могут быть представлены следующей схемой – см. рис. 11.1.

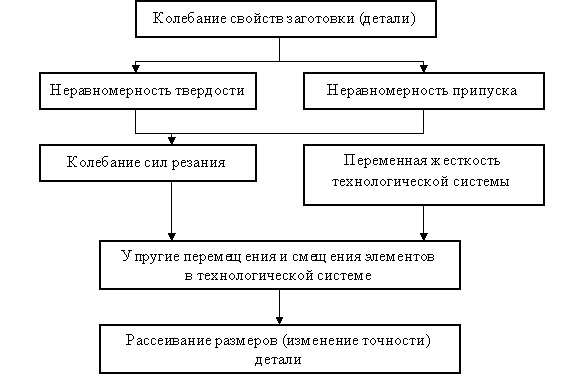
Рис.11.1. Схема формирования упругих перемещений и смещения элементов в технологической системе и влияния их на точность обработки

Жесткость упругой системы СПИД – это отношение составляющей силы резания, направленной по нормали к обрабатываемой поверхности, к смещению лезвия инструмента, установленного на размер в данном направлении.

Таким образом, жесткость системы 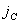равна:

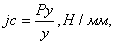
где 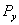– радиальная составляющая силы резания;

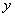- смещение режущей кромки инструмента (деформация упругой системы).

Аналогично выражается жесткость отдельных элементов технологической системы: для суппорта – j _суп, для передней бабки – j _ПБ и т.д.

Жесткость может быть выражена также отношением приращения силы резания 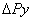к приращению перемещения:

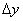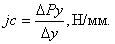
В практических расчетах иногда используют величину, обратную жесткости – податливость .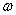

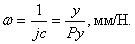
Величина деформации упругой системы равна:

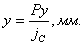
Для определения статической жесткости узла станка производят ряд нагружений, возрастающих от нуля до некоторого предельного значения, которое определяется размерами станка. Для каждого значения нагрузки измеряют смещение узла в направлении действия силы. Затем производят разгружение этого узла, постепенно уменьшая нагрузку и фиксируя остаточные

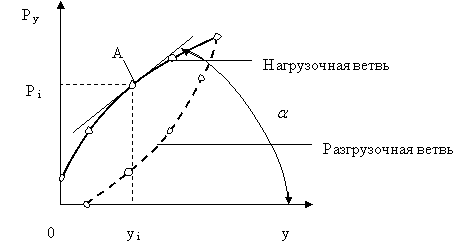
Рис.11.2. Зависимости y = f(P_y) при определении статической жесткости узла станка

отжатия. При нагружении и разгружении строятся зависимости 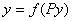– рис.11.2.

При этом нагрузочная и разгрузочная ветви характеристики жесткости обычно не совпадают, т.е. имеет место гистерезис. Площадь петли гистерезиса – работа, затраченная на преодоление сил трения, контактных деформаций и т.д. При повторных циклах нагрузки площадь петли гистерезиса уменьшается вследствие выборки зазоров в стыках деталей при первом нагружении и уменьшения пластического деформирования.

Для оценки жесткости в любой точке (например, в точке А) кривой 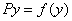необходимо найти производную в данной точке

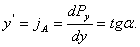
Численно производная равна тангенсу угла наклона касательной к кривой в точке А.

Жесткость станка зависит от его конструкции и от качества сборки. Для многих станков жесткость и податливость регламентированы ГОСТами.

Как показывает практика, статическая жесткость станков в 1,2 – 1,4 раза выше, чем жесткость работающих станков. Поэтому более объективной величиной является динамическая жесткость станков, которая определяется с помощью произвольного метода, который основан на обработке заготовок с переменным припуском и последующих расчетах.

Пример. Определение динамической жесткости токарного станка (рис.11.3).

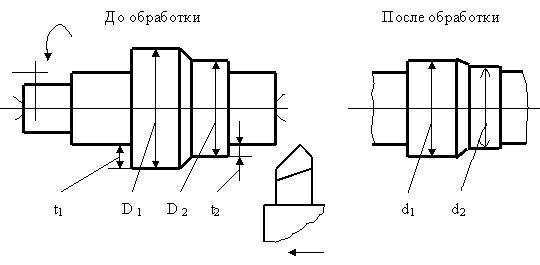
Рис.11.3. Схема испытания токарного станка для определения его динамической жесткости

Пояски диаметрами D ₁ и D ₂ обрабатываются за один рабочий ход при неизменных условиях (подаче, скорости резания и т.д.). Уступ 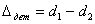, образовавшийся вследствие разных глубин резания и, следовательно, разных отжатий в технологической системе, будет меньш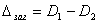е (т.е. ).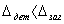

Отношение 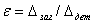называется уточнением. Оно показывает, во сколько раз в результате обработки уменьшилась погрешность заготовки. Уточнение характеризует жесткость технологической системы:

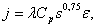
где 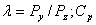- константа (постоянная силы резания). 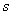– подача.

Жесткость станка зависит и от степени его нагрева. Так, например, по наблюдениям профессора А.В.Худобина жесткость шпиндельной бабки круглошлифовального неработающего станка составляет 15100 Н/мм. После 30 мин его работы на холостом ходу жесткость достигла 22400 Н/мм, т.е. увеличилась на 44%.

Жесткость узлов станков с вращающимися деталями не одинакова в радиальном направлении. Например, по данным Г. Б. Фикс – Марголина для токарных станков характерны следующие круглограммы жесткости шпиндельной группы (j) и упругих перемещений шпинделей (y), подобные приведенным на рис.11.4.

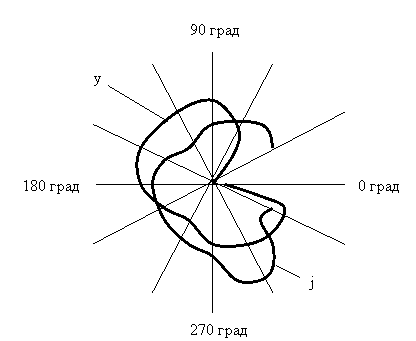
Рис.11.4. Круглограммы жесткости шпиндельной группы (j) и упругих перемещений шпинделей (y) токарных станков

Учитывая, что жесткость технологической системы переменна, и ее значение зависит от многих факторов, проявление которых невозможно предвидеть заранее, ее характеристику следует отнести к разряду случайных величин.

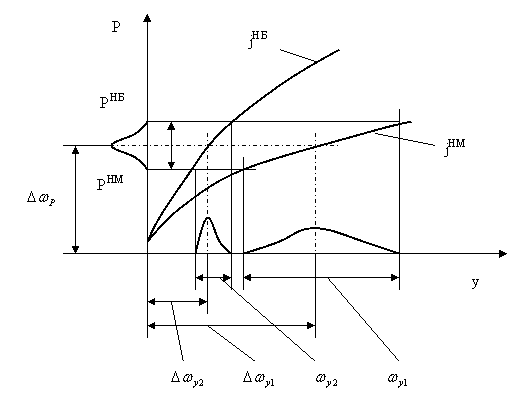
Рис.11.5. Иллюстрация формирования полей рассеяния упругих перемещений в технологической системе

Вследствие рассеяния значений припусков и характеристик свойств материалов заготовок, например, твердости, значения силы резания будут также рассеиваться от P^НМ до Р^НБ. Если при этом учесть, что значения жесткости технологической системы случайны и подлежат рассеянию от j ^НМ до j ^НБ, то даже при стабильном рассеянии значений силы резания, значения поля рассеяния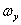 и координаты его середины 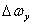не будут оставаться постоянными – рис.11.5. Участок диаграммы между кривыми j ^НМ и j ^НБ на этом рисунке представляет собой поле 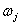рассеяния значений жесткости технологической системы.

Лекция 12

Математическое моделирование точности обработки деталей на станках

Основные факторы, определяющие погрешность обработки деталей

Наличие и формирование погрешности обработки деталей на металлорежущих станках определяются следующими факторами:

1. недостаточная жесткость станка;

2. колебание силы резания из–за неравномерных твердости заготовки и припусков на обработку;

3. неточность станков;

4. погрешности управляющих программ (для станков с ЧПУ, наиболее существенные – погрешности аппроксимации);

5. погрешность установки (базирования и закрепления) заготовки на станке;

6. погрешности настройки инструмента и станка на размер;

7. погрешности обработки, вызванные неточностью инструмента и его износом;

8. тепловые деформации;

9. ошибки рабочего (наладчика, станочника) и т.д.

Действие всех этих факторов, влияющих на точность обработки, приводит к возникновению суммарной погрешности обработки.

Расчетно – аналитический метод определения точности обработки

Согласно этого метода, элементарные погрешности 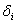определяемые действием каждого из приведенных выше факторов, принимаются практически независимыми друг от друга. Их суммирование производят по вероятностному методу:

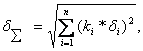
где 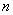– количество учитываемых погрешностей;

Дата добавления: 2014-01-03