
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показатели ряда динамики и методы их расчета
|
|
|
|
Для характеристики скорости и интенсивности изменения уровней ряда динамики рассчитывается система цепных и базисных показателей.
Показатели динамики с переменной базой (цепные показатели) характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате).
Показатели динамики с постоянной базой (базисные показатели) характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относятся базисный уровень, до данного (i-того) периода.
В результате такого сравнения вычисляют систему показателей, в которую включаются абсолютный прирост, коэффициент роста, темп роста, темп прироста и абсолютное значение одного процента прироста.
Абсолютный прирост (D) определяется как разность между двумя уровнями динамического ряда и показывает на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
Базисный абсолютный прирост вычисляется по формуле:
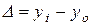 .
.
Цепной абсолютный прирост будет равен:
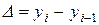 .
.
В этих формулах 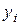 - уровень сравниваемого периода,
- уровень сравниваемого периода, 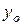 – уровень базисного периода,
– уровень базисного периода, 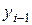 - – уровень предшествующего периода.
- – уровень предшествующего периода.
Коэффициент роста (К) определяется как отношение двух сравниваемых уровней и показывает, во сколько раз данный уровень превышает уровень, принятый за базу сопоставления.
При сравнении с постоянной базой
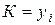 :
: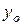 .
.
При сравнении с переменной базой
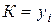 :
: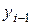 .
.
Коэффициенты роста, выраженные в процентах, называются темпами роста:
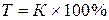 .
.
Темп прироста (t) показывает на сколько процентов уровень данного периода больше (или меньше) уровня, взятого за базу сравнения. Этот показатель может быть рассчитан двояко:
1) как разность между темпом роста и 100%.
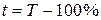 ,
,
2) как отношение абсолютного прироста к уровню, принятому за базу сравнения
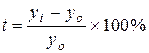 (базисный), или
(базисный), или
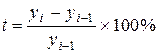 (цепной).
(цепной).
Абсолютное значение одного процента прироста (А) рассчитывается делением абсолютного прироста на темп прироста. Этот показатель вычисляется только как цепной.
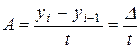 .
.
Если эту формулу преобразовать, то получим следующее выражение:
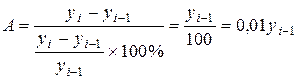 .
.
Для обобщающей характеристики динамики уровней определяют:
1)средние уровни ряда;
2) средние показатели изменения уровней.
Для моментного ряда динамики средний уровень вычисляют по формуле средней хронологической (если промежутки времени между датами одинаковы)
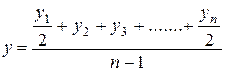 ,
,
где 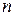 – число уровней ряда,
– число уровней ряда,
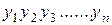 – уровни ряда
– уровни ряда
Если промежутки времени между датами различны, то средний уровень определяется по формуле средней арифметической взвешенной, а в качестве веса (t) берется продолжительность времени между датами (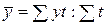 ).
).
Для периодического (интервального) ряда динамики средний уровень ряда рассчитывается по формуле средней арифметической простой:
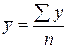 .
.
Средний коэффициент роста определяется по формуле средней геометрической:
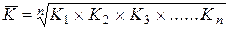 или
или 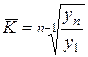 ,
,
где K1, K2, K3, ….. Kn- цепные коэффициенты роста,
средний темп роста: 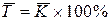 ,
,
средний темп прироста: 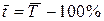 .
.
Проведем расчеты изложенных показателей по данным табл. 7.7.
Таблица 7.7
| Годы | 1995 г. | 1996 г. | 1997 г. | 1998 г. | 1999 г. |
| Количество преступлений на 100 тыс. населения. | 2 800 | 3 105 | 3 318 | 3 456 | 3 497 |
Динамика преступности в районе
| Абсолютные приросты: | |
| цепные | базисные |
| 3 105-2 800=+305, | 3 105-2 800=+305, |
| 3 318-3 105=+213, | 3 318-2 800=+518, |
| 3 456-3 318=+138, | 3 456-2 800=+565, |
| 3 497-3 456=+41. | 3 497-2 800=+697. |
Коэффициент частоты преступлений по сравнению с первым уровнем ряда (1995 г.) ежегодно значительно возрастает, а по сравнению с каждым предшествующим годом рост снижается.
| Коэффициенты роста: | |
| цепные | базисные |
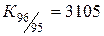 : :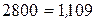 , ,
| 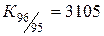 : :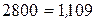 , ,
|
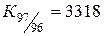 :1,069, :1,069,
| 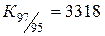 :2 800=1,185, :2 800=1,185,
|
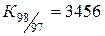 :3 318=1,042, :3 318=1,042,
| 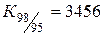 :2 800=1,234, :2 800=1,234,
|
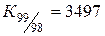 :3 456=1,012. :3 456=1,012.
| 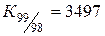 :2 800=1,249. :2 800=1,249.
|
Здесь коэффициент 1,012 показывает, что количество преступлений на 100 тыс. населения в 1999 г. возросло по сравнению с 1998 г. в 1,012 раза, а коэффициент 1,249 говорит о том, что количество преступлений в 1999г. по сравнению с 1995г. возросло в 1,249 раза и т. п.
| Темпы роста: | |
| цепные | базисные |
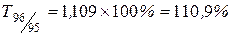 , ,
| 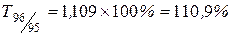 , ,
|
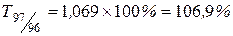 , ,
| 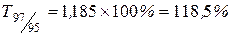 , ,
|
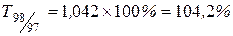 , ,
| 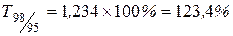 , ,
|
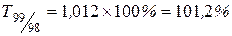 . .
| 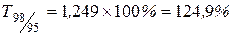 . .
|
Наблюдается снижение цепных темпов роста уровня преступности и рост базисных темпов роста.
| Темпы прироста: | |
| цепные | базисные |
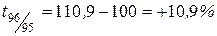 , ,
| 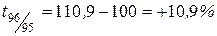 , ,
|
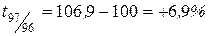 , ,
| 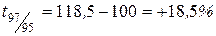 , ,
|
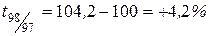 , ,
| 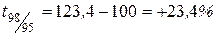 , ,
|
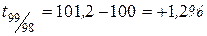 . .
| 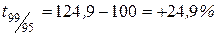 . .
|
Следовательно, уровень преступности в 1999 г. по сравнению с 1998 г. возрос на 1,2%, а по сравнению с 1995 г. на 24,9% и т. д.
Абсолютное значение 1% прироста:
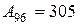 :10,9=28 или 2 800:100=28,
:10,9=28 или 2 800:100=28,
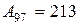 :6,9=31 или 3 105:100=31,
:6,9=31 или 3 105:100=31,
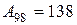 :4,2=33 или 3 318:100=33,
:4,2=33 или 3 318:100=33,
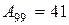 :1,2=34 или 3 456:100=34.
:1,2=34 или 3 456:100=34.
Среднегодовой коэффициент роста:
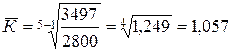 .
.
В среднем за 1995-1999 годы уровень преступности возрастал ежегодно в 1, 057 раза.
Среднегодовой темп роста:
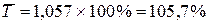 .
.
Среднегодовой темп прироста:
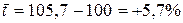 .
.
В среднем уровень преступности ежегодно возрастал на 5,7%.
Средний уровень преступности за 1995-1999 г. г. составил:
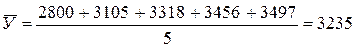
преступлений на 100 тыс. человек населения района.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1854; Нарушение авторских прав?; Мы поможем в написании вашей работы!