Понятие оптимизационных задач и оптимизационных моделей

Лекция 2. Система экономико-математических моделей оптимального планирования и управления

Учебные вопросы

1 Понятие оптимизационных задач и оптимизационных моделей.

2 Методика построения оптимизационной модели.

3 Основные типы линейных экономико-математических моделей.

Оптимизационными задачами в экономике называются экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некото­рого критерия (критериев) варианта использования имею­щихся ресурсов (материальных, временных и пр.).

Общая структура оптимизационной модели состоит из целе­вой функции, принимающей значения в пределах ограничен­ной условиями задачи области (области допустимых решений), и из ограничений, характеризующих эти условия.

Целевая функция в самом общем виде определяется тремя моментами: управляемыми переменными; неуправляемыми переменными (зависящими, например, от внешней среды); видом (формой) зависимости между ними (видом функции).

Целевая функция связывает между собой различные вели­чины модели. Как правило, в качестве цели выбирается эконо­мический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т. д.). Поэтому целевую функцию иногда называют экономической, критериальной.

Критерий оптимальности - признак, на основании которого производится оценка, сравнение альтернатив, классификация объектов и явлений. Критерий оптимальности функционирования экономической системы – это один из возможных критериев (признаков) ее качества, а именно тот признак, по которому функционирование системы признается наилучшим из возможных вариантов ее функционирования. В сфере принятия экономических решений критерий оптимальности – это показатель, выражающий предельную меру экономического эффекта принимаемого хозяйственного решения для сравнительной оценки возможных решений выбора наилучшего из них.

Математической формой критерия оптимальности в экономико-математических моделях является целевая функция, экстремальное значение которой характеризует предельно допустимую эффективность деятельности моделируемого объекта. Одни из критериев - максимизируемые, другие - мини­мизируемые. Из минимизируемых критериев можно выделить такие, как: критерий совокупных затрат труда всех видов, себестоимость продукции и т.д.; из максимизируемых критериев - число наборов конечных продуктов, валовая, конечная, чистая и условно чистая продукция, прибыль, рентабельность и др.

Если обозначить критерий оптимальности через U, управляемые переменные - 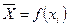, параметры - 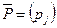, заданные пределы (область) изменения управляемых переменных – М, то общий вид оптимизационной модели будет следующим:

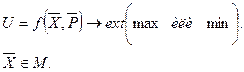(2.1)

Система ограничений состоит из отдельных математичес­ких уравнений или неравенств, называемых балансовыми урав­нениями или неравенствами.

Ограничения подразделяются на:

а) линейные (I и II) и нелинейные (III и IV) (рисунок 2.1) (линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания; если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными);

б) детерминированные (A, В) и стохастические (группы кри­вых С_i) (стохастические ограничения являются возможными, вероят­ностными, случайными) (рисунок 2.2).

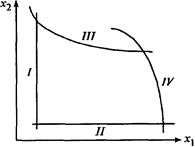Рисунок 2.1 - Линейные и нелинейные ограничения

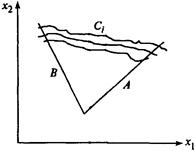Рисунок 2.2 - Детерминированные и сто­хастические ограничения

Оптимизационные задачи вида (2.1) решаются методами математического про­граммирования. Существуют следующие основные методы математического программирования:

- методы линейного программирования требуют наличия системы взаимоувязанных факторов, критерия оценки оптимальности использования ресурсов, позволяют выбрать наилучшие способы использования имеющихся ресурсов;

- методы нелинейного программирования, позволяющие решать задачи, в которых цель описывается нелинейной гладкой функцией, а ограничения задачи - нелинейными неравенствами;

- методы стохастического программирования, которыми решаются задачи планирования, если все или хотя бы часть параметров являются случайными величинами;

- методы динамического программирования, с помощью которых решаются линейные и нелинейные задачи, представленные в виде пошагового процесса;

- методы целочисленного программирования, с помощью которых решаются задачи с условием целочисленности переменных;

- методы выпуклого программирования;

- исследование операций;

- геометрическое программирование и др.

Выбор методов математического программирования для решения оптимизационных задач определяется видом целевой функции f, видом ограничений, определяющих область М, и специальными ограничениями на управляемые переменные (например, требованием их целочисленности, неотрицательности и т.д.).

Решением экономико-математической модели, или допу­стимым планом, называется набор значений неизвестных, ко­торый удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, называемый оптимальным, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремаль­ные значения целевой функции. План, для которого целевая функция модели имеет экстремальное значение, называют экс­тремальным планом, или экстремальным решением.

Таким образом, для принятия оптимального решения лю­бой экономической задачи необходимо построить ее экономи­ко-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптималь­ности и решение (оптимальный план).

Дата добавления: 2014-01-03