Экономико-математическая постановка задач массового обслуживания

Классификация СМО

Наиболее распространенные в прак­тике типы СМО представлены в виде классификационной структуры на рисунке 5.2.

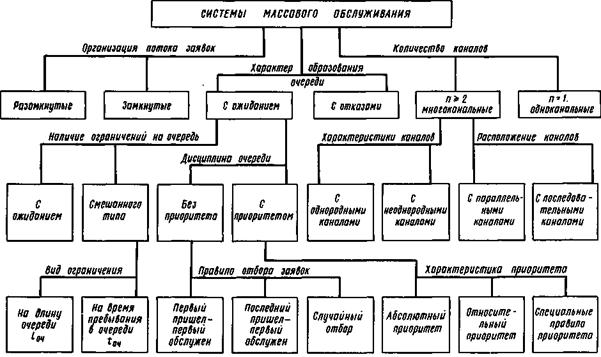
Рисунок 5.2 - Классификационная структура СМО

Системы массового обслуживания (СМО) классифицируют­ся по разным признакам.

По числу каналов обслуживания (n) СМО разделяются на одноканальные (n = 1) и многоканальные (n > 2). К одноканальным СМО в торговле можно отнести практически любой ва­риант локального обслуживания, например выполняемый одним продавцом, товароведом, экономистом, торговым аппаратом.

В зависимости от взаимного расположения каналов системы подразделяются на СМО с параллельными и с последовательными каналами. В СМО с параллельными каналами входной поток заявок на обслуживание является общим, и поэтому заявки в очереди мо­гут обслуживаться любым свободным каналом. В таких СМО оче­редь на обслуживание можно рассматривать как общую.

В многоканальной СМО с последовательным расположением каналов каждый канал может рассматриваться как отдельная одноканальная СМО, или фаза обслуживания. Очевидно, выходной по­ток обслуженных заявок одной СМО является входным потоком для последующей СМО.

В зависимости от характеристик каналов обслуживания много­канальные СМО подразделяются на СМО с однородными и неод­нородными каналами. Отличие состоит в том, что в СМО с однородными каналами заявка может обслуживаться любым свободным ка­налом, а в СМО с неоднородными каналами отдельные заявки обслу­живаются только специально для этой цели предназначенными ка­налами, например кассы для оплаты одного-двух предметов в универ­саме.

В зависимости от возможности образования очереди СМО под­разделяются на два основных типа: СМО с отказами обслуживания и СМО с ожиданием (очередью) обслуживания.

В СМО с отказами возможен отказ в обслуживании, если все каналы уже заняты обслуживанием, а образовывать очередь и ожи­дать обслуживания нельзя. Примером такой СМО является стол заказов в магазине, в котором прием заказов осуществляется по телефону.

В СМО с ожиданием, если заявка находит все каналы обслужи­вания занятым, то она ожидает, пока не освободится хотя бы один из каналов.

СМО с ожиданием подразделяются на СМО с неограниченным ожиданием или с неограниченной очередью l_оч и временем ожида­ния Т_оч и СМО с ограниченным ожиданием, в которых накладыва­ются ограничения или на максимально возможную длину очереди (max l_оч = m), или на максимально возможное время пребывания заявки в очереди (max Т_оч = Т_огр), или на время работы системы.

В зависимости от организации потока заявок СМО подразде­ляются на разомкнутые и замкнутые.

В разомкнутых СМО выходной поток обслуженных заявок не связан с входным потоком заявок на обслуживание. В замкнутых СМО обслуженные заявки после некоторой временной задержки Т_з снова поступают на вход СМО и источник заявок входит в состав СМО. В замкнутой СМО циркулирует одно и то же конечное число потен­циальных заявок, например, посуда в столовой — через торговый зал, мойку и раздачу. Пока потенциальная заявка циркулирует и не преобразовалась на входе СМО в заявку на обслуживание, считается, что она находится в линии задержки.

Типовые варианты СМО определяются также и установленной дисциплиной очереди, которая зависит от преимущества в обслу­живании, т. е. приоритета. Приоритет отбора заявок на обслужива­ние может быть следующий: первый пришел — первый обслужен; последний пришел — первый обслужен; случайный отбор. Для СМО с ожиданием и обслуживанием по приоритету возможны следующие виды: абсолютный приоритет, например для сотрудников контроль­но-ревизионного управления, министра; относительный приоритет, например для директора торга на подведомственных ему предприятиях; специальные правила приоритета, когда обслуживание за­явок оговорено в соответствующих документах. Существуют и другие типы СМО: с поступлением груп­повых заявок, с каналами разной производительности, со смешан­ным потоком заявок.

Совокупности СМО разных типов, объединенные последо­вательно и параллельно, образуют более сложные структуры СМО: секции, отделы магазина, универсама, торговой организации и т. п. Такое моделирование позволяет выявить существенные связи в тор­говле, применить методы и модели теории массового обслуживания для их описания, оценить эффективность обслуживания и разра­ботать рекомендации по его совершенствованию.

Правильная экономико-математическая постановка задачи в значительной степени определяет эффективность рекомендаций по совершенствованию массового обслуживания в торговле, в сфере услуг и т.д. В связи с этим необходимо наблюдать за обслуживанием, выявлять сущест­венные связи проблемы, формировать цели и определять экономи­ческие критерии оценки работы СМО. В качестве общего, интег­рального критерия могут выступать затраты, с одной стороны, СМО как обслуживающей системы, а с другой — заявок, кото­рые могут иметь разную базу. Например, для товаров, поступающих в торго­вую сеть, этот критерий связан со временем и скоростью их обраще­ния и интенсивностью поступления денежных средств в банк.

Рассмотрим моделирование СМО в торговле. Оно должно включать анализ затрат времени в процессе обслуживания, например продавцов или населения в актах продажи-покупки товаров. Затем с помощью соответствующих методов и приемов необходимо строить модели свя­зи с другими показателями СМО торговли.

Например, особенностью показателей для СМО с отказами яв­ляется то, что время ожидания заявок в очереди Т_оч = 0. Поскольку в этом случае существование очереди невозможно, то l_оч = 0 и, следовательно, вероятность ее образования р_оч = 0. По числу заявок k определяются режим работы системы, ее состояние: при k = 0 — простой каналов, при 1<k<n — обслуживание заявок, при k>n — обслуживание и отказ. Показателями таких СМО являются: вероятность отказа в обслуживании р_отк, вероятность обслуживания р_обс, среднее время простоя канала T_пp, среднее число соответственно занятых и свободных каналов N_з и N_св, среднее вре­мя обслуживания Т_обс, абсолютная пропускная способность А.

Для СМО с неограниченным ожиданием характерно, что веро­ятность обслуживания заявки р_обс = 1, поскольку длина очереди и время ожидания начала обслуживания не ограничены, т. е. фор­мально 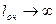и 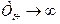. В таких системах возможны следующие режимы работы: при k = 0 наблюдается простой каналов обслужи­вания, при 1<k<n — обслуживание и при k>n — обслуживание и очередь. Показателями эффективности таких СМО являются: среднее число заявок в очереди l_оч, среднее число заявок в системе N_сист, среднее время пребывания заявки в системе T_сис, абсолютная про­пускная способность А.

В СМО с ожиданием с ограничением на длину очереди mах l_оч = m; если число заявок в системе k = 0, то наблюдается простой каналов. При 1<k<n — обслуживание, при n<k<n+m — обслуживание и очередь и при k > n+m — обслуживание, очередь и отказ в обслуживании. Показателями эффективности таких СМО являются вероятность отказа в обслуживании р_отк, вероятность обслуживания р_обс, среднее число заявок в очереди l_оч, среднее число заявок в системе N_сист, среднее время пребывания заявки в си­стеме T_сис, абсолютная пропускная способность А.

В процессе постановки задачи необходимо раскрыть взаимо­связи показателей эффективности СМО, которые по своей базовой принадлежности можно разделить на две группы, которые образуют две совокупности.

Первая группа показателей связана с издержками обращения торговли С_ио, которые определяются числом занятых обслужива­нием каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки каналов, эффективностью их использования, пропускной способностью СМО и т.п.

Вторая группа показателей определяется издержками соб­ственно заявок С_из, поступающих на обслуживание, которые обра­зуют входящий поток и связаны с такими показателями, как длина очереди, время ожидания обслуживания, вероятность отказа в об­служивании, время пребывания заявки в СМО и др.

Обобщенным показателем эффективности СМО, включающим требования и возможности обеих групп, может быть крите­рий экономической эффективности, включающий как издержки обращения С_ио, так и издержки заявок С_из, которые будут иметь оптимальное значение при минимуме общих затрат С. На этом основании целевую функцию задачи можно записать так: С = (С_ио + С_из) → min.

Поскольку издержки обращения включают затраты, связанные с эксплуатацией СМО (С_экс) и простоем каналов обслуживания (С_пр), а издержки заявок включают потери, связанные с уходом необслуженных заявок (С_нз) и с пребыванием в очереди (С_оч), то целевую функцию можно переписать с учетом общих показателей таким образом:

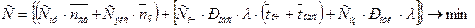. (5.9)

В зависимости от поставленной задачи управляемыми показателями могут быть: количество каналов обслуживания, организация кана­лов обслуживания (параллельно, последовательно, смешанным образом), дисциплина очереди, приоритет в обслуживании заявок, взаимопомощь между каналами и др. Часть показателей в задаче фигурирует в качестве неуправляемых, они обычно являются исход­ными данными. Следует заметить, что в качестве критерия эффек­тивности в целевой функции может быть товарооборот торгового предприятия или, например, рентабельность. Тогда, очевидно, оптимальные значения управляемых показателей СМО находятся уже при их максимальном значении и необходимо соответствующим образом провести преобразования целевой функции.

После построения целевой функции необходимо определить условия решения задачи, т. е. найти ограничения, установить ис­ходные значения показателей, выделить неуправляемые показатели и построить или подобрать совокупность моделей взаимосвязи всех показателей для анализируемого типа СМО, чтобы в конечном итоге найти оптимальные значения управляемых показателей, на­пример, количество продавцов, кассиров, грузчиков, фасовщиков, объемы складских помещений, размещение товаров в торговом зале и др.

Дата добавления: 2014-01-03