Экономико-математическая модель межотраслевого баланса

Принципиальная схема межотраслевого баланса

Принципиальная схема межотраслевого баланса производ­ства и распределения совокупного общественного продукта в стоимостном выражении приведена в таблице 8.1.

Таблица 8.1 - Принципиальная схема межотраслевого баланса (МОБ)

Потребляющие отрасли Производящие отрасли				…	n	Конечный продукт (Yi)	Валовой продукт (Xi)
	х11	х12	х13	…	х1n	y1	х1
	х21	х22	х23	…	x2n	y2	х2
	х31	х32	х33	…	х3n	y3	х3
…	…	…	…	I	…	II	…
n	хn1	хn2	хn3	…	хnn	yn	хn
Амортизация (cj)	c1	c2	c3	…	cn	IV
Оплата труда (nj)	v1	v2	v3	III	vn
Чистый доход (mj)	m1	m2	m3	…	mn
Валовой продукт (Xj)	x1	x2	x3	…	xn

В основу этой схемы положено разделение совокупного продукта на две час­ти: промежуточный и конечный продукт; все народное хозяйст­во представлено в виде совокупности n отраслей (имеются в виду чистые отрасли), при этом каждая отрасль фигурирует в балансе как производящая и как потребляющая.

Рассмотрим схему МОБ в разрезе его крупных составных ча­стей. Выделяются четыре части, имеющие различное экономи­ческое содержание; они называются квадрантами баланса и на схеме обозначены римскими цифрами.

Первый квадрант МОБ – это шахматная таблица межотрас­левых материальных связей. Показатели, помещенные на пе­ресечениях строк и столбцов, представляют собой величины межотраслевых потоков продукции и в общем виде обозначают­ся х_ij, где i и j - соответственно номера отраслей производящих и потребляющих. Так, величина x₃₂ понимается как стоимость средств производства, произведенных в отрасли с номером 3 и потребленных в качестве материальных затрат в отрасли с но­мером 2. Таким образом, первый квадрант по форме представ­ляет собой квадратную матрицу порядка n, сумма всех элемен­тов которой равняется годовому фонду возмещения затрат средств производства в материальной сфере.

Во втором квадранте представлена конечная продукция всех отраслей материального производства, при этом под ко­нечной понимается продукция, выходящая из сферы производ­ства в область конечного использования (на потребление и на­копление). В таблице 8.1 этот раздел дан укрупненно в виде одного столбца величин Y_i; в развернутой схеме баланса конечный про­дукт каждой отрасли показан дифференцированно по направле­ниям использования: на личное потребление населения, общественное потребление, на накопление, возмещение потерь, экс­порт и др. Итак, второй квадрант характеризует отраслевую ма­териальную структуру национального дохода, а в развернутом виде характеризует также распределение национального дохо­да на фонд накопления и фонд потребления, структуру потреб­ления и накопления по отраслям производства и потребителям.

Третий квадрант МОБ также характеризует национальный доход, но со стороны его стоимостного состава как сумму чистой продукции и амортизации; чистая продукция понимается при этом как сумма оплаты труда и чистого дохода отраслей. Сумму амортизации (c_j) и чистой продукции (v_j + m_j) некоторой j -ой от­расли будем называть условно-чистой продукцией этой отрасли и обозначать в дальнейшем Z_j.

Четвертый квадрант баланса находится на пересечении столбцов второго квадранта (конечной продукции) и строк тре­тьего квадранта (условно-чистой продукции). Этим определяет­ся содержание квадранта: он отражает конечное распределение и использование национального дохода. В результате перерас­пределения первоначально созданного национального дохода об­разуются конечные доходы населения, фирм и предприятий, го­сударства. Данные четвертого квадранта важны для отражения в межотраслевой модели баланса доходов и расходов населения, источников финансирования капиталовложений, текущих за­трат непроизводственной сферы, для анализа общей структуры конечных доходов по группам потребителей. Очень важным является тот факт, что об­щий итог четвертого квадранта, так же как второго и третьего, должен быть равен созданному за год национальному доходу.

Таким образом, в целом межотраслевой баланс в рамках еди­ной модели объединяет балансы отраслей материального произ­водства, баланс совокупного общественного продукта, балансы национального дохода, финансовый, доходов и расходов населе­ния. Следует особо отметить, что валовая продукция отраслей, хотя она и не входит в рассмотренные выше четыре квадранта, представлена на принципиальной схеме МОБ в двух местах: в виде столбца, расположенного справа от второго квадранта, и в виде строки ниже третьего квадранта. Эти столбец и строка вало­вой продукции замыкают схему МОБ и играют важную роль как для проверки правильности заполнения квадрантов (т. е. про­верки самого баланса), так и для разработки экономико-матема­тической модели межотраслевого баланса. Если, как показано на схеме, обозначить валовой продукт некоторой отрасли буквой Х с нижним индексом, равным номеру данной отрасли, то можно за­писать два важнейших соотношения, отражающих сущность MOB и являющихся основой его экономико-математической модели.

Во-первых, рассматривая схему баланса по столбцам, мож­но сделать очевидный вывод, что итог материальных затрат лю­бой потребляющей отрасли и ее условно-чистой продукции ра­вен валовой продукции этой отрасли. Данный вывод можно записать в виде следующего соотношения:

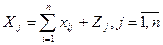(8.1)

Соотношение (8.1) охватывает систему из n уравнений, отражающих стоимостной состав продукции всех отраслей ма­териальной сферы.

Во-вторых, рассматривая схему МОБ по строкам для каж­дой производящей отрасли, можно видеть, что валовая про­дукция той или иной отрасли равна сумме материальных за­трат потребляющих ее продукцию отраслей и конечной про­дукции данной отрасли:

. (8.2)

Формула (8.2) описывает систему из n уравнений, кото­рые называются уравнениями распределения продукции от­раслей материального производства по направлениям испо­льзования.

Просуммируем по всем отраслям уравнения (8.1), в резуль­тате получим

(8.3)

Аналогичное суммирование уравнений (8.2) дает:

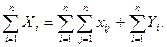(8.4)

Левые части обоих равенств равны между собой, так как представляют собой весь валовой общественный продукт. Пер­вые слагаемые правых частей этих равенств также равны меж­ду собой, их величина равна итогу первого квадранта. Следова­тельно, должно соблюдаться соотношение

(8.5)

Левая часть уравнения (8.5) есть сумма третьего квадранта, а правая часть – итог второго квадранта. В целом же это уравне­ние показывает, что в межотраслевом балансе соблюдается важнейший принцип единства материального и стоимостного состава национального дохода.

Основу информационного обес­печения модели межотраслевого баланса составляет техноло­гическая матрица, содержащая коэффициенты прямых мате­риальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели межотраслевого баланса. Предполагается, что для про­изводства единицы продукции в j -й отрасли требуется опреде­ленное количество затрат промежуточной продукции i -й отрас­ли, равное а_ij. Оно не зависит от объема производства в j -й от­расли и является довольно стабильной величиной во времени.

Величины а_ij называются коэффициентами прямых материа­льных затрат и рассчитываются следующим образом:

. (8.6)

Таким образом, имеет место определение 1. Коэффициент прямых материальных затрат а_ij показывает, какое количество продукции i -й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j -й отрасли.

С учетом формулы (8.6) систему уравнений баланса (8.2) можно переписать в виде

. (8.7)

Если ввести в рассмотрение матрицу коэффициентов пря­мых материальных затрат , вектор-столбец валовой продукции Х и вектор-столбец конеч­ной продукции Y:

, ,

то система уравнений (8.7) в матричной форме примет вид

X = AX + Y. (8.8)

Система уравнений (8.7), или в матричной форме (8.8) назы­вается экономико-математической моделью межотраслевого баланса (моделью В. Леонтьева) или моделью «затраты - вы­пуск». С помощью этой модели можно выполнять три варианта расчетов:

1) задав в модели величины валовой продукции каждой от­расли (X_i), можно определить объем конечной продукции каж­дой отрасли (Y_i):

Y = (Е - А) ∙ Х; (8.9)

2) задав величины конечной продукции всех отраслей (Y_i), можно определить величины валовой продукции каждой отрасли (Х_i):

X = (E – A)^-1 ∙ Y; (8.10)

3) задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продук­ции, можно найти величины конечной продукции первых от­раслей и объемы валовой продукции вторых; в этом варианте расчета удобнее пользоваться не матричной формой модели (8.8), а системой линейных уравнений (8.7).

В формулах (8.9) и (8.10) Е обозначает единичную матрицу n -го порядка, a (E - A)^-1 обозначает матрицу, обратную к матри­це (Е - А). Если определитель матрицы (Е - А) не равен нулю, т. е. эта матрица невырожденная, то обратная к ней матрица су­ществует. Обозначим эту обратную матрицу через B = (E – A)^-1, тогда систему уравнений в матричной форме (8.10) можно запи­сать в виде

X = B ∙ Y. (8.11)

Элементы матрицы В будем обозначать через b_ij, тогда из матричного уравнения (8.11) для любой i -й отрасли можно получить следующее соотношение:

, (8.12)

где ΔХ_i и ΔY_j - изменения (приросты) величин валовой и конеч­ной продукции соответственно.

Из соотношений (8.12) следует, что валовая продукция вы­ступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты b_ij, которые показыва­ют, сколько всего нужно произвести продукции i -й отрасли для выпуска в сферу конечного использования единицы продукции j -й отрасли. В отличие от коэффициентов прямых затрат а_ij ко­эффициенты b_ij называются коэффициентами полных материа­льных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают коли­чество средств производства, израсходованных непосредствен­но при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производ­ство продукта не прямо, а через другие (промежуточные) средства производства.

Дадим определение коэффициента полных затрат (опреде­ление 2): коэффициент полных материальных затрат b_ij пока­зывает, какое количество продукции i -й отрасли нужно произ­вести, чтобы с учетом прямых и косвенных затрат этой продук­ции получить единицу конечной продукции j -й отрасли.

Коэффициентами полных материальных затрат можно по­льзоваться, когда необходимо определить, как скажется на ва­ловом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей.

Литература

1 Абчук В.А. Экономико-математические методы: Элементарная математика и логика. Методы исследования операций. – СПб.: Союз, 1999. – 320 с.

2 Багриновский К.А., Матюшонок В.М. Экономико-математические методы и модели (микроэкономика): Учебное пособие для вузов. – М.: Изд-во РУДН, 1999. – 183 с.: ил.

3 Балашевич В.А., Андронов A.M. Экономико-математическое моделирование производственных систем: Учебное пособие для вузов. – Мн.: Унiверсiтэцкае, 1995. – 240 с.

4 Бережная Е.В., Бережной В.И. Математические методы моделиро­вания экономических систем: Учеб. пособие. – М.: Финансы и статистика, 2001. – 368 с.: ил.

5 Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах. – СПб.: БХВ – Санкт-Петербург, 1999. – 336 с.

6 Дорохина Е.Ю., Халиков М.А. Моделирование микроэкономики. Учебное пособие для вузов / Под общ. ред. Н.П. Тихомирова. – М.: Издательство «Экзамен», 2003. – 224 с.

7 Костевич Л.С. Математическое программирование: Информационные технологии оптимальных решений: Учебное пособие. – Мн.: Новое знание, 2003. – 424с.

8 Кузнецов А.В. и др. Высшая математика: Математическое программирование: Учебник / Кузнецов А.В., Сакович В.А., Холод Н.И. // Под общ. ред. А.В. Кузнецова. – Мн.: Выш. шк., 1994. – 286 с.

9 Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: ВНV–Санкт-Петербург, 1997. – 384 с., ил.

10 Лабскер Л.Г., Бабешко Л.О. Теория массового обслуживания в экономической сфере: Учебное пособие для вузов. – М.: Банки и биржи, ЮНИТИ, 1998. – 319 с.

11 Практикум по курсу «Экономико-математические методы и модели»: Учебное пособие / С.Л. Масанский, О.В. Сидорова. – Могилев: МГУП, 2005. – 120 с.

12 Скриба С.И., Скриба Н.Н. Экономико-статистическое моделирование и прогнозирование средствами MS Excel: Учебное пособие. – Мн.: БГЭУ, 2002. – 171 с.

13 Спирин А.А., Фомин Г.П. Экономико-математические методы и модели в торговле: Учебное пособие для экономических и товароведных факультетов торговых вузов. – М.: Экономика, 1988. – 149 с.

14 Федосеев В.В., Эриашвили Н.Д. Экономико-математические методы и модели в маркетинге: Учебное пособие для вузов / Под редакцией В.В. Федосеева. – М.: ЮНИТИ-ДАНА, 2001. – 159 с.

15 Черняк А.А., Новиков В.А., Мельников О.И., Кузнецов А.В. Математика для экономистов на базе Mathcad. – СПб.: БХВ-Петербург, 2003. – 496 с.

16 Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2000. – 367 с.

17 Экономико-математические методы и модели. Компьютерные технологии решения: Учебное пособие / И.Л. Акулич, Е.И. Велесько, П. Ройш, В.Ф. Стрельчонок. – Мн.: БГЭУ, 2003. – 348 с.

18 Экономико-математические методы и модели: Учебное пособие / Н.И. Холод, А.В. Кузнецов, Я.Н. Жихар и др. // Под общ. ред. А.В. Кузнецова. - Мн.: БГЭУ,1999. – 413 с.

Дата добавления: 2014-01-03