Момент импульса. Момент силы

Мы видели, что механические свойства замкнутой системы не изменяются при ее параллельном переносе в пространстве. Это свойство является следствием однородности пространства, то есть отсутствием каких-либо выделенных точек пространства, физические свойства системы не должны изменяться также и при ее поворотах в пространстве, ввиду отсутствия в пространстве выделенных направлений, что означает изотропность пространства. Оказывается, что неизмен­ность физических свойств системы при ее поворотах в пространстве также приводит к сохранению некоторой новой механической величины — момента импульса системы.

Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которую действуют также внешние силы. Уравнения движения частиц имеют вид:

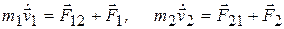1.74

Умножим первое уравнение векторно слева на r₁, а второе на r₂.

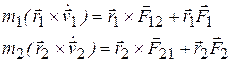1.75

Поскольку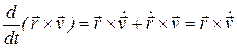, т.к. 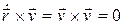и F₁₂ = ‑ F₂₁,

получим

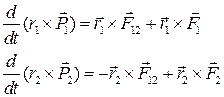1.76.

Сложим полученные уравнения:

.

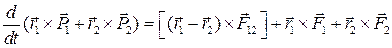Векторы r₁ - r₂ и F₁₂ коллениарны, поэтому

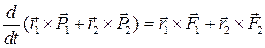. 1.77.

Если система замкнута 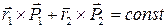. Еще одна сохраняющаяся величина, которую называют моментом импульса.

Примеры:

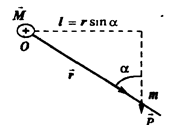
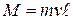
Момент импульса материальной точки, движущейся по прямой, относительно оси О

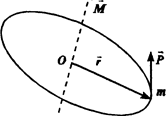
M = mvr

Момент импульса точки, движущейся по окружности

Моментом силы называют 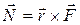1.77

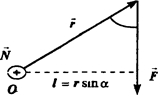
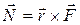N = r · F · sinα = F ·l 1.78.

Момент силы. относительно точки О

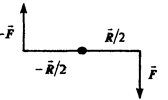
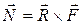; N = R · F · sinα. 1.79

Пара сил.

Продифференцируем 1.74 по времени:

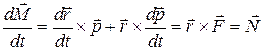1.80

Поступательное движение	Вращательное движение	Поступательное движение	Вращательное движение
Основной закон динамики	Работа и мощность
F ∙Δ t = mv 2 ‑ mv 1	M ∙Δ t = J ∙ω2 ‑ J ∙ω1	A = F ∙ s	A =М∙φ
F = m ∙ a	M = J ∙ε	N = F ∙ v	N = M ∙ω
Закон сохранения	Кинетическая энергия
момента импульса	импульса

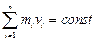
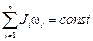
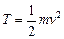
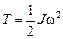
Дата добавления: 2014-01-03