Бесконечно малые и бесконечно большие последовательности (величины)

▼Последовательность 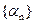называется бесконечно малой величиной, если для любого сколь угодно малого положительного числа 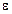можно подобрать такой номер N, что, начиная с этого номера (т.е. для всех ), будет выполнено неравенство

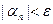. (8) ▲

Нельзя смешивать бесконечно малую величину с малым числом. Любое малое число 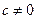неизменно и для него всегда можно указать другое положительное число 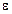, такое, что | c | будет не менее .

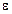aЛюбое малое число с, неравное нулю, не является бесконечно малой величиной.

Свойства бесконечно малых последовательностей

1. Сумма конечного числа бесконечно малых есть также величина бесконечно малая.

2. Произведение бесконечно малой на постоянную есть бесконечно малая последовательность (т.к. всякое постоянное можно рассматривать как ограниченную величину).

3. Произведение нескольких бесконечно малых является бесконечно малой.

Термин «бесконечно большая величина», как и термин «бесконечно малая величина», определяет не размер величины, а характер изменения её числового значения.

▼ Последовательность { β_n } называется бесконечно большой, если для любого сколь угодно большого числа М найдётся такой номер N, что для всех n, начиная с этого номера, выполняется неравенство

| β_n |> M. (9) ▲

За геометрический образ бесконечно большой величины можно принять точку М, абсцисса которой равна х, перемещающуюся по оси Ох в одном направлении (вправо или влево) или удаляющуюся от начала О на всё большее и большее расстояние попеременно то вправо, то влево.

Дата добавления: 2014-01-03