
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
АЛУ на базе логических запоминающих устройств (ЛЗУ)
|
|
|
|
При решении информационно-логических задач значительная часть времени уходит на выполнение логических операций. Одним из эффективных способов повышения производительности ЭВМ при выполнении логических операций является реализация их в специализированных структурах, получивших название логических ЗУ. Это возможно благодаря свойству практически всех ЗЭ реализовывать поразрядную дизъюнкцию при записи слова в ячейку без предварительной ее очистки. Кроме того, на регистре RGD можно получить поразрядное отрицание. Поскольку дизъюнкция и отрицание являются функционально полной системой операций, то любая поразрядная логическая операция может быть выполнена непосредственно в ЗУ. Любое ЗУ, ЗЭ которого обладают таким свойством, можно практически без каких-либо дополнительных аппаратурных затрат преобразовать в логическое. Для этого достаточно внести такие изменения в блок управления, чтобы наряду с обычной записью слов можно было осуществить запись в ячейку без предварительной ее очистки. Операция такого типа протекает примерно в 2 раза быстрее, так как отсутствует такт очистки. Реализация логических операций непосредственно в ЗУ использовалась в ЭВМ БЭСМ-6.
Процедура выполнения других поразрядных логических операций сложнее. Например, выполнение поразрядной конъюнкции по формуле 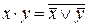 требует нескольких обращений к ЗУ в последовательности, приведенной в табл. 9.1.
требует нескольких обращений к ЗУ в последовательности, приведенной в табл. 9.1.
Таблица 9.1
| Операция | Содержимое ячеек | ||
| RGD | a | b | |
| 0. Исходное состояние | x | y | |
| 1. (a) ® RGD | x | y | |
2. (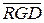 )® a )® a
| 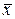
| y | |
| 3. (b) ® RGD | y | 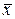
| |
4. (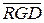 )® a )® a
| 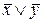
| ||
| 5. (a) ® RGD | 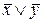
| ||
6. (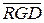 )® a )® a
| 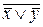
|
Логические возможности ЗУ значительно расширяются, если к РШ можно подключать прямые и инверсные выходы RGD. Рассмотрим статический ЗЭ на основе триггера (T), выполненного на МДП-транзисторах (рис. 9.6). Транзисторы VT3 и VT4 служат в качестве сопротивлений нагрузки для VT1 и VT2, выполняют функции элементов И и работают в режиме двусторонней проводимости. При чтении возбуждается АШ, открывая VT5 и VT6. Запись осуществляется по совпадению сигналов на АШ и РШ (0 или 1), т. е. система выборки 2 D.
 |
Рис. 9.6. Статический запоминающий элемент на МДП-транзисторах
Обозначим через X и Y цифры, записанные в ЗЭ и соответствующем разряде RGD. Возможны два варианта двухканальной связи RGD ® РШ:
1. 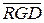 ® РШ0 и RGD ® РШ1;
® РШ0 и RGD ® РШ1;
2. 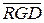 ® РШ1 и RGD ® РШ0,
® РШ1 и RGD ® РШ0,
и четыре варианта одноканальной связи:
3. 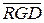 ® РШ0; 4.
® РШ0; 4. 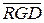 ® РШ1;
® РШ1;
5. RGD ® РШ0; 6. RGD ® РШ1.
Первый вариант характеризуется обычным подключением RGD к РШ (нулевой выход RGD подключается к РШ0, а единичный выход – к РШ1). При втором варианте производится инверсное включение RGD. Остальные варианты получаются из первых двух путем отключения одной из шин. Функции, реализуемые при записи Y в ЗЭ, хранящий X, приведены в табл. 9.2.
Таблица 9.2
| X | Y | Реализуемые функции | |||||
| X | Y | Y | 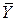
| XY | 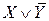
| 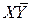
| 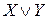
|
Из этой таблицы следует, что кроме поразрядной дизъюнкции и инверсии за одно обращение к памяти могут выполняться еще три двухместные операции. За счет дальнейшего усложнения АЦ, РЦ и накопителя можно добиться однотактного выполнения любой двухместной операции. Кроме повышения быстродействия ЭВМ логические ЗУ (ЛЗУ) также применяются и для создания ЭВМ с малыми аппаратурными затратами. Минимизацию этих затрат удается произвести за счет выполнения в ЛЗУ не только логических, но и арифметических операций, благодаря чему от АЛУ можно отказаться. Это удается осуществить, если имеется возможность записывать слова в накопитель со сдвигом на один разряд влево или вправо. Известно, что любая арифметическая операция сводится к микрооперациям сложения и сдвига. В свою очередь сложение сводится к поразрядным операциям:
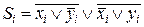 ,
,
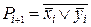 .
.
В табл. 9.3 приведен пример реализации сложения многоразрядных чисел путем выполнения поразрядных операций и сдвига.
Таблица 9.3
| Микрооперация | X = 0,011010110010 Y = 0,001100101111 |
| Сложение Сдвиг Сложение Сдвиг Сложение Сдвиг Сложение Сдвиг Сложение | P 1= 0,001000100010 S 1= 0,010110011101 2 P 1= 0,010001000100 P 2= 0,010000000100 S 2= 0,000111011001 2 P 2= 0,100000001000 P 3= 0,000000001000 S 3= 0,100111010001 2 P 3= 0,000000010000 P 4= 0,000000010000 S 4= 0,100111000001 2 P 4= 0,000000100000 P 5= 0,000000000000 S 5= 0,100111100001 P 5= 0, END |
Так как любая арифметическая операция сводится к сдвигам и суммированиям, то все функции АЛУ можно реализовать в ЛЗУ. Известно, что микропрограммное устройство управления может быть построено на базе ПЗУ. Функции ЛЗУ шире, чем у ПЗУ, поэтому реализация микропрограммного устройства управления возможна и на базе ЛЗУ. Следовательно, ЛЗУ может совмещать в себе функции трех основных устройств ЭВМ: арифметико-логического, запоминающего и управляющего, что позволяет строить на основе ЛЗУ простые ЭВМ.
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 736; Нарушение авторских прав?; Мы поможем в написании вашей работы!