Представление и обработка данных в виде графов

Графы формально описывают множество близких ситуаций. Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связыва­ющие их дороги. Перекрестки являются вершинами графа, а дороги — его ребрами. Графы могут быть ориентированы (подобно улицам с односторонним движением) или взвешены, когда каждой дороге приписана стоимость путешествия по ней (если, например, дороги платные).

С формальной точки зрения граф представляет собой упорядоченную пару мно­жеств G = (V, Е), первое из которых состоит из вершин (узлов) графа, а второе — из его ребер. Ребро связывает между собой две вершины. При работе с графами часто решается вопрос, как проложить путь из ребер от одной вершины графа к другой. В этом случае говорят о движении по ребру, что означает переход из вершины А гра­фа в другую вершину В, связанную с ней ребром АВ (ребро графа, связывающее две вершины, для краткости обозначается этой парой вершин). В этом случае говорят, что ребро А примыкает к ребру В или что эти две вершины соседние.

Граф может быть ориентированным или нет. Ребра неориентированного гра­фа, чаще всего называемого просто графом, можно проходить в обоих направле­ниях (рис. 14.26). В этом случае ребро — это неупорядоченная пара вершин, его концов.

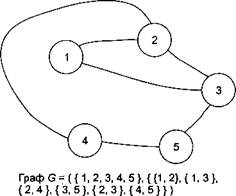
Рис. Неориентированный граф

В ориентированном графе, или орграфе, ребра представляют собой упорядочен­ные пары вершин: первая вершина — это начало ребра, вторая — его конец (рис.).

Полный граф — это граф, в котором каждая вершина соединена со всеми осталь­ными. Количество ребер в полном графе без петель с N вершинами равно (N² - N)/2. В полном ориентированном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направ

Подграф (V_S,E_s) графа или орграфа (V,E) состоит из некоторого подмножества вершин, VsÌV,h некоторого подмножества ребер, их соединяющих, E_s Ì Е.

Путь в графе или орграфе — это последовательность ребер, по которым можно поочередно проходить. Другими словами, путь из вершины А в вершину В начина­ется в Л и проходит по набору ребер до тех пор, пока не будет достигнута вершина В. С формальной точки зрения путь из вершины V_x в вершину V_y — это последова­тельность ребер графа:

V_xV_x+1, V_x+1 V_x+2, ….. V_y-1 V_y

Необходимо, чтобы любая вершина встречалась на таком пути не более, чем однажды. У всякого пути есть длина — количество ребер в нем. Длина пути АВ, ВС_} CD, DE равна 4.

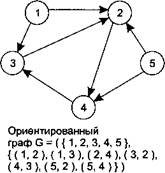
Рис. Ориентированный граф

Граф или орграф называется связным, если всякую пару узлов можно соединить по крайней мере одним путем. Цикл — это путь, который начинается и кончается в одной и той же вершине. В ациклическом графе или орграфе циклы отсутствуют. Связный ациклический граф называется неукорененным деревом. Структура неукорененного дерева такая же, как и у дерева, только в нем не выделен корень. Однако каждая вершина неукорененного дерева может служить его корнем.

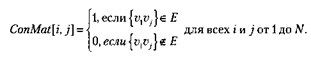
Рис. 14.28. Матрицы примыканий графа и орграфа

Информацию о графах или орграфах в пригодном для обработки компьютер­ными алгоритмами виде можно хранить двумя способами: в виде матрицы при­мыканий и в виде списка примыканий\

Матрица примыканий обеспечивает быстрый доступ к информации о ребрах графа, однако, если в графе мало ребер, эта матрица будет содержать гораздо боль­ше пустых клеток, чем заполненных. Длина списка примыканий пропорциональна числу ребер в графе, однако при пользовании списком время получения информа­ции о ребре увеличивается.

Матрица примыканий ConMat графа G = (V,E) с числом вершин | V| = N запи­сывается в виде двухмерного массива размером N х ЛГ. В каждой ячейке [у] этого массива записано значение 0 за исключением лишь тех случаев, когда из вершины Vi в вершину Vj ведет ребро, и тогда в ячейке записано значение 1:

Список примыканий ConList графа G = (V, Е) с числом вершин | V| = ЛГ записыва­ется в виде одномерного массива длины N, каждый элемент которого представляет собой ссылку на список. Такой список приписан каждой вершине графа и содержит по одному элементу на каждую вершину графа, соседнюю с данной.

На рис. 14.29 изображен список примыканий для орграфа, изображенного на рис. 14.27. На этом рисунке буквами L_VN обозначены вершины графа, а буквами v_N — те вершины, к которым направлены выходящие из данной вершины ребра.

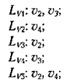
Рис. 14.29. Список примыканий для орграфа

При работе с графами часто приходится выполнять некоторое действие по од­ному разу с каждой из вершин графа, например, когда некоторую порцию инфор­мации следует передать каждому из компьютеров в сети. При этом нерационально посещать какой-либо компьютер дважды. Аналогичная ситуация возникает, если нужно собирать, а не распространять информацию.

Подобный обход можно совершать двумя способами. При обходе в глубину проход по выбранному пути осуществляется настолько глубоко, насколько это возможно, а при обходе по уровням происходит равномерное движение вдоль всех возможных направлений.

Дата добавления: 2014-01-03