Фононы в одномерном кристалле

Масса узлов m, равновесные положения определяются узлами решетки 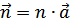, где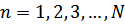

Пусть 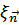– смещение атома из положения равновесия. В потенциальную энергию дают вклад только соседние атомы

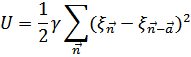
Кинетическая энергия выражается через скорости смещения 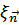c помощью функции

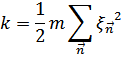
Введем периодические (циклические) граничные условия

Одномерной решетке соответствует зона Бриллюэна с границами

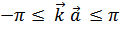
Внутри этой зоны располагается N штук волновых векторов

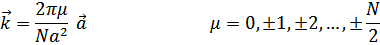
От смещений отдельных атомов 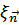удобно перейти к новым обобщенным координатам 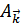, которые характеризуют коллективные движения атомов, соответствующие определенным значениям .

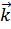Для этого введем преобразование

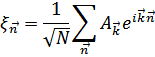
Суммирование по всем возможным 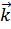внутри зоны Бриллюэна

Для того, чтобы 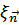была вещественна, новые переменные должны удовлетворять условиям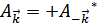

Используя определение векторов 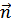, 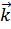можно показать

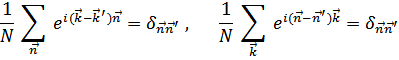
Тогда можно получить обратное преобразование

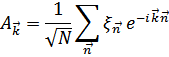
В результате, энергия выражается через новые коллективные переменные

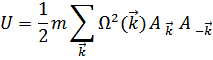
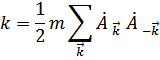
Где

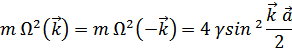
Классическая функция Лагранжа имеет вид

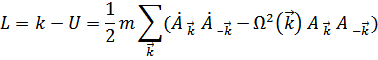
Откуда получаем выражение для обобщенных импульсов, соответствующих обобщенным координатам .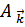

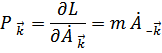
Импульс 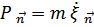, сопряженный смещению 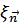, позволяет представить обобщенный импульс в виде

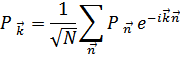
В результате получим классическую энергию как функцию обобщенных координат 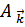и обобщенных импульсов

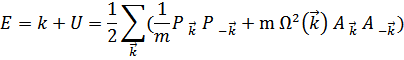
Переход к квантовой механике сводится к замене 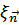, 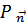соответствующими операторами, удовлетворяющим перестановочным соотношениям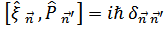

Тогда обобщенные координаты и импульсы будут удовлетворять соотношениям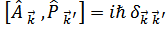

Оператор энергии имеет вид

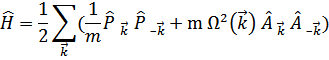
От операторов 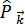, 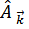удобно перейти к новым операторам 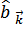,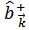с помощью соотношений

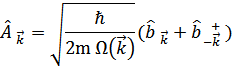
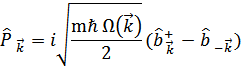
Новые операторы должны удовлетворять коммутационным соотношениям (чтобы выполнялось соотношение между 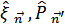) Это операторы Бозе.

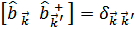
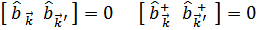
В результате гамильтониан преобразуется к диагональному виду

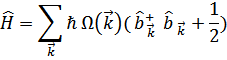
Основное состояние кристалла описывается функцией

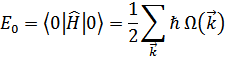
В этом состоянии энергия имеет наименьшее значение.

Энергия кристалла в квантовом состоянии 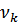равна

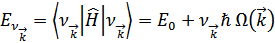
Далее учтем, что из определения 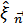, 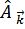получим

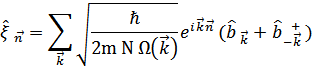
Это позволит вычислить среднее смещение n-ого атома из положения равновесия в том же квантовом состоянии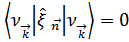

В то же время среднее значение квадрата смещения не зависит от номера атома

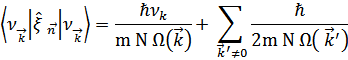
Второе слагаемое характеризует вклад «нулевых колебаний», когда все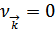

При 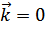имеем смещение кристалла как целого. При этом 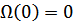.Поэтому при 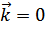колебания атомов отсутствуют, и это значение исключено из суммы.

В сумму же входят только такие 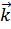, абсолютная величина которых 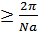(чтобы выполнялось неравенство для зоны Бриллюэна )

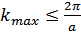Тогда

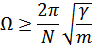
Таким образом, стационарные возбужденные состояния кристалла распределены по всему кристаллу и характеризуются волновым вектором 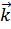(квазиимпульс 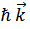, энергия 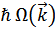). Эти возбужденные состояния называются фононами.

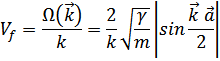
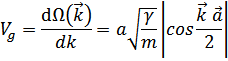
Длинноволновые возбуждения 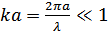характеризуются величинами

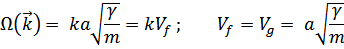
Длинноволновые возбуждения можно рассматривать как упругие волны в среде. Скорость упругих волн (скорость звука) определяется выражением 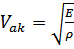, где 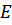– модуль Юнга 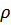– плотность. В нашем случае

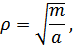
а модуль Юнга (отношение силы к вызванной ею упругой деформации)

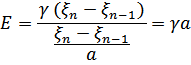
Таким образом,

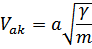
Следовательно, рассмотренные нами элементарные возбуждения в пределе 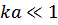совпадают с акустическими волнами в упругой среде. Поэтому эти возбуждения называются акустическими фононами.

ТЕМА №2

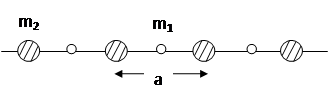Фононы в одномерном кристалле с двумя атомами в элементарной ячейке.

положение элементарных ячеек определяется вектором решетки .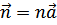

Смещение атомов из равновесных положений 0, в элементарной ячейке с вектором 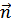обозначим 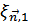и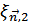

Кинетическая энергия имеет простой вид

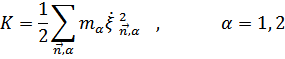
В гармоническом приближении

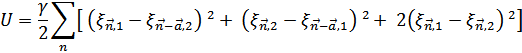
Периодические граничные условия есть

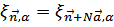
Далее та же процедура, что и ранее. Разница заключается в том, что теперь имеется две частоты

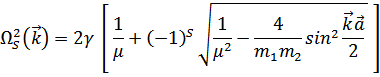
Где 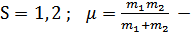приведенная масса двух атомов.

Две функции 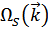определяют частоту двух ветвей колебаний.

В длинноволновом приближении 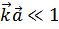эти функции имеют вид

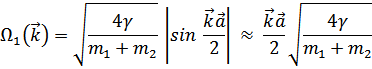
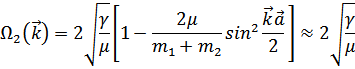
Функция 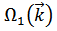совпадает с прежней 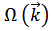(частота акустических волн в решетке с одним атомом в элементарной ячейке, если его масса равна (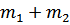)). Поэтому 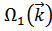называют акустической ветвью колебаний.

Функция 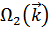характеризует колебания, частоты которых не стремятся к нулю при приближении вектора 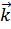к центру зоны Бриллюэна. Они определяют оптическую ветвь колебаний.

Если 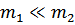, то при приближении 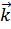к границе зоны Бриллюэна (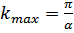) обе функции достигают максимального значения

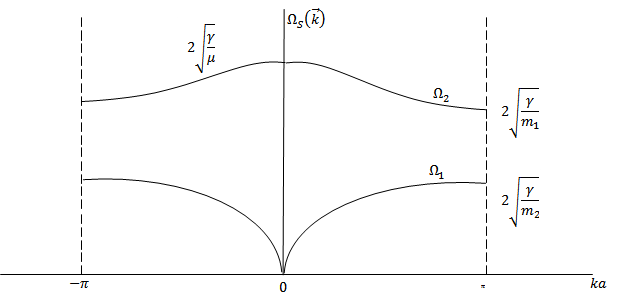
Дальнейший анализ показывает, что для акустической ветви атомы в элементарной ячейке колеблются в одинаковых направлениях.

В оптической ветви они совершают колебания в противоположных направлениях.

К чему это приводит:

В ионных кристаллах в элементарную ячейку входят ионы с противоположными зарядами. Поэтому оптические колебания связаны с большим изменением электрического дипольного момента ячейки. Они определяют оптические свойства кристалла в данной области частот. Отсюда и название этой ветви колебаний.

Дата добавления: 2014-01-03