Автоколебания. Параметрические колебания

6.1. Автоколебания.

Потеря энергии системой, совершающей собственные колебания, приводит к их затуханию. Если к осциллятору подводить энергию посредством внешней гармонической силы, то он будет совершать колебания с частотой, вообще говоря, отличающейся от собственной (вынужденные колебания).

Можно создать такое устройство, в котором осциллятор сам регулирует подвод энергии, чтобы компенсировать её потерю на трение. Если за период колебаний энергия, приобретаемая осциллятором из внешнего источника, равна энергии, затрачиваемой на преодоление сил трения, то осциллятор совершает незатухающие колебания. Такие самоподдерживающиеся колебания называются автоколебаниями.

При малом трении за период в систему извне поступает лишь небольшая доля полной энергии осциллятора, и автоколебания с большой точностью являются гармоническими, причем их частота очень близка к частоте собственных колебаний.

При большом трении за каждый период от внешнего источника подводится значительная часть полной энергии осциллятора, и поэтому колебания сильно отличаются от гармонических - период этих колебаний не совпадает с периодом собственных колебаний.

Примеры:

1) Автоколебания маятника. Маятник, подвешенный на оси во вращающейся втулке.

2) Релаксационные колебания.

Частным случаем автоколебаний являются релаксационные колебания. Характер изменения величин, происходящий в системе со временем, весьма своеобразен. Система медленно накапливает изменения, а затем очень резко возвращается в начальное состояние, после чего процесс накопления изменений повторяется. С древних времен известны релаксационные колебания высоты столба жидкости, которые проиллюстрированы на рисунке.

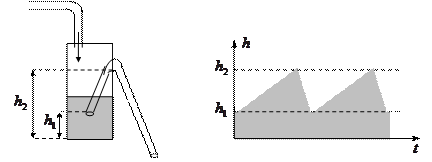В сосуд, медленно заполняемый

водой, введена широкая трубка-

сифон, по которой вода может

вытекать из сосуда. Когда

уровень воды достигает нижней

стенки сифонной трубки (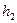) в

её верхней части, она заполняет

трубку и быстро выливается по

всему её поперечному сечению,

понижая уровень воды в сосуде

до высоты 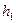. После этого начинается новый цикл заполнения сосуда водой.

6.2. Параметрическое возбуждение колебаний.

Характеристики или свойства колебательных систем описываются величинами, называемыми параметрами. Так, математический маятник в постоянном поле силы тяжести характеризуется одним параметром - длиной. Если изменять параметр в определенном такте с колебаниями, то можно сообщить маятнику энергию и тем самым поддерживать колебания в незатухающем режиме. Представим, что нить математического маятника под действием внешних сил укорачивается вблизи нижнего положения, а вблизи крайних положений удлиняется. Работа внешних сил при укорочении нити вблизи положения равновесия будет больше работы, производимой маятником при удлинении вблизи каждого из крайних положений. Это связано с изменением натяжения нити, которое достигает максимума в нижнем положении. Т.о., колебательная система за счет работы внешних сил дважды за период будет получать энергетическую подпитку.

Такое возбуждение и поддержание колебаний называется параметрическим.

Хорошо известным примером параметрического возбуждения и поддерживания колебаний служит катание на качелях. Качающийся приседает, когда качели находятся в верхней точке траектории, и выпрямляется при прохождении нижней точки. Работа, совершаемая при выпрямлении в нижней точке траектории качелей, по абсолютной величине больше работы, которая совершается при приседании в верхних точках. Разность совершенных работ равна разности энергий при качании, поэтому качели раскачиваются. Если при постоянной амплитуде качаний произведенная работа полностью затрачивается на работу против сил трения, то качания поддерживаются в незатухающем режиме.

6.3. Колебания связанных систем.

Система, участвующая в колебательном процессе, может обладать несколькими (многими) степенями свободы. В механике число степеней свободы определяется как число не зависящих друг от друга возможных перемещений системы. Отсюда следует, что даже такая идеализированная колебательная система, как математический маятник, обладает двумя степенями свободы, поскольку может совершать колебания в двух взаимно перпендикулярных плоскостях (в вертикальных плоскостях, ориентированных по осям x и y).

Связанной системой называют систему со многими степенями свободы, между которыми имеются связи, обеспечивающие возможность обмена энергией между различными степенями свободы.

При рассмотрении колебательных процессов часто используется термин нормальные колебания, или нормальные моды. Нормальными колебаниями (нормальными модами) называют собственные (свободные) колебания систем с постоянными параметрами, в которых отсутствуют как потери, так и приток энергии извне.

Каждому из нормальных колебаний может быть сопоставлена своя нормальная частота. Число нормальных частот равно числу степеней свободы механической системы.

Оказывается, что, несмотря на сложность колебательного процесса в связанной системе, её движение всегда может быть представлено как суперпозиция нормальных колебаний с нормальными частотами связанной системы.

Т.о., задача исследования колебательного движения связанных систем сводится к нахождению их нормальных колебаний и определению нормальных частот. Иногда указать нормальные колебания позволяют достаточно простые соображения. Однако в большинстве случаев эта задача оказывается достаточно сложной. Отметим, что существуют общие методы нахождения нормальных частот, но их изучение выходит за рамки нашей программы. Поэтому мы ограничимся рассмотрением сравнительно простого примера, который в то же время позволяет достаточно хорошо проиллюстрировать подход к решению задачи о колебательном движении связанных систем.

Итак, рассмотрим в качестве примера связанной системы два маятника, соединенных между собой пружиной.

Как уже было отмечено, обычный маятник может совершать колебания

в двух взаимно перпендикулярных плоскостях, проходящих через точку его

подвеса, т.е. обладает двумя степенями свободы. Если один из связанных

пружиной маятников вывести из положения равновесия, отклонив его

одновременно в плоскости маятников и в перпендикулярном этой

плоскости направлении, то после начала колебаний первого маятника начнет

раскачиваться второй маятник, также обладающий своими двумя

степенями свободы. Всего такая система обладает четырьмя степенями

свободы, на которые наложена посредством пружины связь.

Колебания маятников в такой системе будут происходить с

изменяющимися во времени амплитудами. В целом будет наблюдаться довольно сложная картина движения маятников, возникающая в результате обмена энергией между маятниками, образующими единую замкнутую механическую систему.

Однако, как было сказано выше, движение связанной системы маятников может быть представлено как суперпозиция четырех нормальных колебаний с нормальными частотами связанной системы.

Посмотрим теперь, как можно определить нормальные частоты этой системы.

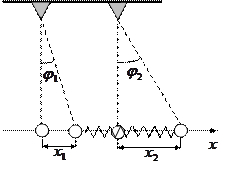
Состояние системы в любой момент времени характеризуется заданием положений обоих маятников. Обратимся сначала к движению маятников в плоскости, перпендикулярной линии, соединяющей точки подвеса, и покажем, что любое возможное состояние системы может быть представлено как сумма двух последовательно реализованных состояний:

1. оба маятника отклонены от положения равновесия в одну и ту же сторону на один и тот же угол;
2. маятники отклонены в разные стороны на один и тот же угол.

Справедливость этого утверждения следует из приведенного рисунка.

Действительно, положения маятников 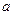и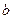

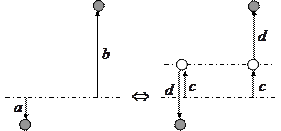могут быть представлены как 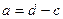и

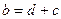, соответственно.

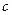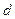Простейшие отклонения и называются

нормальными. Очевидно, что маятники

отведенные из положения равновесия на один

и тот же угол (в одну или в разные стороны)

будут совершать колебания с одинаковой

частотой. Поэтому каждому нормальному

отклонению можно сопоставить свою нормальную частоту, соответственно, 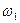и 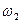. Произвольное же колебание двух маятников в рассматриваемой плоскости может быть представлено в виде суммы двух гармонических колебаний с нормальными частотам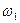и и .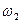

Совершенно аналогично рассматриваются колебания маятников, совершаемые в вертикальной плоскости, проходящей через линию, соединяющую точки подвеса.

В рассматриваемом примере две из четырех нормальных частот являются просто частотами собственных колебаний маятников (они одинаковы, если одинаковы маятники), а две другие – частотами колебаний маятников при симметричных отклонениях от положения равновесия в противоположные стороны при наличии силы упругости со стороны пружины.

Полностью движение системы из двух маятников с четырьмя степенями свободы может быть представлено как суперпозиция четырех нормальных колебаний с соответствующими нормальными частотами.

То, что некоторые нормальные частоты, как, например, в рассматриваемой колебательной системе, могут быть одинаковыми, не меняет существа задачи и используемого подхода.

Перейдем теперь к математическому описанию колебаний в рассматриваемой связанной системе, состоящей из двух маятников, ограничившись рассмотрением их малых колебаний в вертикальной плоскости, проходящей через точки подвеса. Другими словами, мы рассмотрим движение связанной системы с двумя степенями свободы.

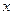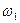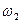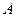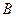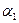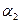При малых колебаниях маятников можно пренебречь их вертикальными смещениями и рассматривать одномерное движение системы вдоль горизонтальной оси . Тогда решение задачи формально сводится к сложению двух колебаний с нормальными частотами и , амплитудами и и начальными фазами и , совершаемыми вдоль оси 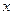. Поэтому можем записать

(7.107)

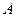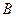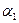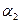Постоянные , , и определяются из начальных условий, записанных для отклонений 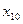, 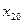и скоростей 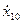, 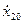маятников в момент времени :

; ;

; .

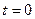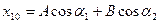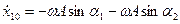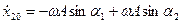Однако решить эту же задачу можно, непосредственно используя законы динамики. Этот путь интересен, в первую очередь, тем, что он позволяет лучше понять физическое содержание рассматриваемой задачи.

Пусть 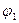и 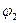– углы отклонения маятников от вертикалей,

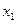а и 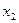– смещения колеблющихся точек относительно их

положений равновесия. Длины маятников одинаковы и равны .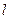

Далее, когда точки одновременно находятся в положении

равновесия, соединяющая их пружина не деформирована.

При малых колебаниях уравнения движения маятников

имеют вид (7.10):

; ,

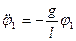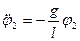а отклонения колеблющихся точек от положения равновесия

могут быть выражены как

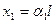и .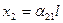

Тогда уравнения движения материальных точек без учета их связи пружиной имеют вид:

; .

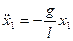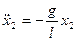При упругой деформации пружины возникают силы, действующие на материальные точки и пропорциональные её удлинению :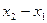

,

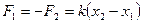где 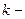коэффициент жесткости пружины.

С учетом сил связи (пружины) уравнения движения точек имеют вид:

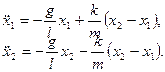(7.108)

Складывая и вычитая уравнения (7.108), имеем

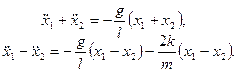(7.109)

Перепишем уравнения (7.109) в виде

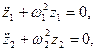(7.110)

где

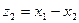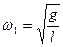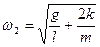, , , . (7.111)

Решение уравнений (7.110) нам хорошо известно (7.50), поэтому можем записать

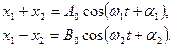
Отсюда получаем

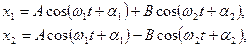(7.112)

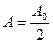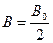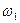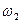где мы положили и , а частоты и , определяемые формулами (7.112), являются нормальными частотами колебаний связанной системы маятников, движение которых происходит только в вертикальной плоскости, проходящей через точки подвеса, т.е. реализуются две степени свободы из четырех.

.

Дата добавления: 2014-01-03