Основые характеристики сигналов

Одной из составляющих анализа сигналов является измерение их основных количественных характеристик. К таким характеристикам прежде всего относят энергию и мощность сигнала.

____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Если к резисто­ру с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет равна

.

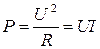За время T в этом резисторе выделится тепловая энергия, равная

Мгновенная мощность (instantaneous power).

______________________________________________________________________________________________________________________________________________________________________________________________________

Энергия, выделяющаяся за время T:

____________________________________________________________________________________________________________________________________

Средняя мощность (average power) за заданный промежуток времени:

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

____________________________________________________________________________________________________________________________________

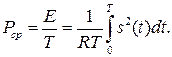
При сопротивлении нагрузки R = 1 получим определения энергии, мгновенной мощности и средней мощности, принятые в теории сигналов:

- энергия, выделившаяся за время Т,

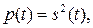- мгновенная мощность, (2.1)

- средняя мощность.

Замечание. Данные параметры иногда называют удельной мощностью и энергией, чтобы подчеркнуть подразумеваемое при этом единичное значение сопротивления нагрузки. Здесь мощность имеет размерность [B²] а энергия — [В² · с].

________________________________________________________________________________________________________________________________________________________________________________________________

Если энергия сигнала бесконечна, можно определить его среднюю мощность на всей временной оси. Для этого нужно воспользоваться формулой (2.1) и выпол­нить предельный переход, устремив интервал усреднения в бесконечность:

(2.2)

Если этот интеграл сходится, то средняя мощность конечна!

Покажем это на примере периодического сигнала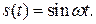

Действительно:

.

Квадратный корень из средней мощности дает среднеквадратическое (действую­щее) значение сигнала (английский термин — root mean square, RMS):

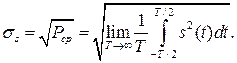(2.3)

______________________________________________________________________________________________________________________________________________________________________________________________________

Примеры 2.1 и 2.2 иллюстрируют вычисление энергии и мощности дискретных сигналов в MATLAB.

Пример 2.1.

n=[-5:5];%primer 2.1

x=2*impseq(-2,-5,5)-impseq(4,-5,5);

subplot(2,2,1);stem(n,x); title('Sequence 2.1a')

xlabel('n'); ylabel('x(n)');

Ex1=sum(x.*conj(x))

n=[0:20];

x1=n.*(stepseq(0,0,20)-stepseq(10,0,20));

x2=10*exp(-0.3*(n-10)).*(stepseq(10,0,20)-stepseq(20,0,20));

x=x1+x2;

subplot(2,2,2);stem(n,x); title('Sequence 2.1b')

xlabel('n'); ylabel('x(n)');

Ex2=sum(x.*conj(x))

n=[0:50];

x=cos(0.04*pi*n)+0.2*randn(size(n));

subplot(2,2,3);stem(n,x); title('Sequence 2.1c')

xlabel('n'); ylabel('x(n)');

Ex3=sum(x.*conj(x))

n=[-10:9]; x=[5,4,3,2,1];

xtilde=x'*ones(1,4);

xtilde=(xtilde(:))';

subplot(2,2,4);stem(n,xtilde); title('Sequence 2.1d')

xlabel('n'); ylabel('xtilde(n)');

Ex4=sum(xtilde.*conj(xtilde))

function [x,n]=impseq(n0,n1,n2)

n=[n1:n2];x=[(n-n0)==0];

function [x,n] = stepseq(n0,n1,n2)

n=[n1:n2];

x=[(n-n0)>=0];

Дата добавления: 2014-01-03