Ввод, сложение и вычитание векторов

Вектор-столбцы и вектор-строки

Работу с массивами начнем с простого примера — вычисления суммы векторов

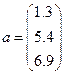
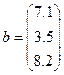
Для хранения векторов используйте массивы а и b. Введите массив а в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:

>>а = [1.3; 5.4; 6.9]

a=

1.3000

5.4000

6.9000

Замечание

Следует запомнить, что точка с запятой в конце выражения используется для подавления вывода результата выражения на экран. Оказывается, что этот символ предназначен и для разделения элементов векторов.

Так как введенное выражение не завершено точкой с запятой, то MatLab тематически вывела значение переменной а. Введите теперь второй вектор, подавив вывод на экран

>>b = [7.1; 3.5; 8.2];

Для нахождения суммы векторов используется знак +. Вычислите сумму, запишите результат в массив с и выведите его элементы в командное окно:

>> с = а + b

8.4000

8.9000

15.1000

Узнайте размерность и размер массива а при помощи встроенных функций

ndims и size: >>ndims(a)

ans=

size(a) ans =

3 1

Итак, вектор а хранится в двумерном массиве а размерностью три на один (вектор-столбец из трех строк и одного столбца). Аналогичные операции можно проделать и для массивов b и с. Заметьте, что числа в MatLab представляются в виде двумерного массива один на один. Отсюда должно стать понятно, почему при сложении векторов используется тот же знак плюс, что и для сложения чисел. Естественно, для нахождения разности векторов следует применять знак минус, с умножением дело обстоит несколько сложнее.

Замечание

Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.

Особенность MatLab представлять все данные в виде массивов является очень удобной. Пусть, например, требуется вычислить значение функции sin сразу для всех элементов вектора с (который хранится в массиве с) и записать результат в вектор d. Используйте следующий оператор присваивания:

» d = sin(c)

d =

0.8546

0.5010

0.5712

Итак, встроенные в MatLab элементарные функции приспосабливаются к виду аргументов; если аргумент является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива. Убедитесь в этом еще на одном примере. Если необходимо найти квадратный корень из элементов вектора d со знаком минус, то достаточно записать:

>>sqrt(d)

ans =

0 + 0.9244i

0 + 0.7078i

0 + 0.7558i

Оператор присваивания не использовался, поэтому MatLab записала ответ в стандартную переменную ans.

Ввод вектор-строки осуществляется в квадратных скобках, однако элементы следует разделять пробелами или запятыми. Операции сложения, вычитания и вычисление элементарных функций от вектор-строк производятся так же, как и с вектор-столбцами, в результате получается вектор-строка того же размера, что и исходные.

>> s1 = [3 4 9 2]

s1 =

3 4 9 2

>> s2 = [5 3 3 2]

>>s2 =

5 3 3 2

>>s3 = s1 + s2

s3=

8 7 12 4

>>s4=log(s3)

s4 =

2.0794 1.9459 2.4849 1.3863

Выясните, в каких массивах хранятся вектор-строки. Для этого можно использовать функции ndims и size или команду whos:

» whos

Name Size Bytes Class

s1 1x4 32 double array

s2 1x4 32 double array

s3 1x4 32 double array

s4 1x4 32 double array

Итак, вектор-строки s1, s2, s3 и s4 содержатся в двумерных массивах размерностью один на четыре. Для определения длины векторов или вектор-строк служит встроенная функция length:

>>length(s1)

ans=

Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:

>>vl = [1; 2];

>>v2 = [3; 4; 5];

>>v = [vl; v2]

v=

Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:

» vl = [1 2];

»v2 = [3 4 5];

»v = [vl v2]

v =

1 2 3 4 5

Дата добавления: 2014-01-03