Группировка данных. Вариационный ряд

Следующим шагом в изучении признака является группировка – разделение членов совокупности на группы, в которых члены совокупности принимают либо одни и те же значения, либо значения внутри определенного интервала. Способы группировки зависят от вида признака.

· Группировка данных качественного признака

Пример 2. При опросе туристической группы (20 человек) выяснено, что среди них 5 человек городские жители, 5 – сельские. Данные сгруппированы в Таблице 2.

Таблица 2.

Группировка туристов по месту жительства.

Туристы	городские	сельские	всего
Количество

· Для группировки данных в случае количественного дискретного признака располагают все варианты в порядке возрастания и указывают частоту, с которой они встречаются в данной совокупности.

Пример 3. Имеются данные об оценках 24 студентов, полученных ими на экзамене

Минимальное значение оценки х_min – 2, максимальное х_max – 5. Подсчитав частоту, с которой встречаются варианты, оформим таблицу (см. Таблицу 3).

Таблица 3.

хi	ni

Таблица, позволяющая судить о распределении частот между вариантами, называется дискретным вариационным рядом.

· Группировка данных в случае количественного непрерывного признака (или дискретного признака, когда число вариант велико).

В этом случае строят интервальный вариационный ряд. Для построения интервального вариационного рядя определяют величину (ширину) интервала, составляют шкалу интервалов и в соответствии с ней группируют результаты наблюдений. Для определения ширины интервала используют формулу: 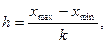где h – ширина интервала, х_min и х_max – минимальная и максимальная варианты, k – число групп; или формулу Стэрджеса, позволяющую определить оптимальную величину интервала 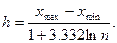Если h оказывается дробным числом, то за ширину интервала принимают либо ближайшее целое число, либо ближайшую несложную дробь. За начало первого интервала рекомендуется принимать величину, равную (х_min – h/2), второго интервала (x_min + h/2) и т.д. Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или больше х_max.

Для подсчета числа вариант, входящих в тот или иной интервал, удобно, просматривая последовательно статистические данные, проставлять черточки справа от соответствующего интервала. При этом в интервал включаются варианты больше левой границы и меньше или равные правой границе. Число вариант, попавших в один интервал, называется частотой интервала.

Пример 4. В результате измерения веса 25 кроликов различной породы были получены значения, представленные в таблице:

3,2	4,5	5,2	5,6	6,6
3,8	4,7	5,2	5,7	6,3
4,1	4,9	5,3	5,8	6,4
4,3	5,0	5,3	5,8	6,7
4,3	5,1	5,4	5,9	7,3

Из таблицы видно, что х_max = 7,3, x_min = 3,2. Определим величину интервала 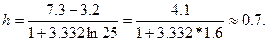Можно взять h=1. тогда левой границей первого интервала будет число x_min – h/2=3,2-0,5=2,7.

Таблица 4.

Распределение кроликов по весу

Интервалы	ni (частоты)
2.7-3.7
3.7-4.7
4.7-5.7
5.7-6.7
6.7-7.7

n = 25

Дата добавления: 2014-01-03