Функции корреляции сигналов

Функции корреляции сигналов применяются для интегральных количественных оценок формы сигналов и степени их сходства друг с другом.

Автокорреляционные функции (АКФ) сигналов (correlation function, CF). Применительно к детерминированным сигналам с конечной энергией АКФ является количественной интегральной характеристикой формы сигнала, и представляет собой интеграл от произведения двух копий сигнала s(t), сдвинутых относительно друг друга на время t:

B_s(t) = 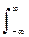s(t) s(t+t) dt. (2.25)

Как следует из этого выражения, АКФ является скалярным произведением сигнала и его копии в функциональной зависимости от переменной величины значения сдвига t. Соответственно, АКФ имеет физическую размерность энергии, а при t = 0 значение АКФ непосредственно равно энергии сигнала:

B_s(0) =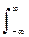s(t)² dt = E_s.

Функция АКФ является непрерывной и четной. В последнем нетрудно убедиться заменой переменной t = t-t в выражении (2.25):

B_s(t) =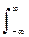s(t-t) s(t) dt = 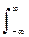s(t) s(t-t) dt = B_s(-t). (2.25')

С учетом четности, графическое представление АКФ производится только для положительных значений t. На практике сигналы обычно задаются на интервале положительных значений аргументов от 0-Т. Знак +t в выражении (2.25) означает, что при увеличении значений t копия сигнала s(t+t) сдвигается влево по оси t и уходит за 0, что требует соответствующего продления сигнала в область отрицательных значений аргумента. А так как при вычислениях интервал задания t, как правило, много меньше интервала задания сигнала, то более практичным является сдвиг копии сигнала влево по оси аргументов, т.е. применение в выражении (2.25) функции s(t-t) вместо s(t+t).

По мере увеличения значения величины сдвига t для финитных сигналов временное перекрытие сигнала с его копией уменьшается и скалярное произведение стремятся к нулю.

Пример. На интервале (0,Т) задан прямоугольный импульс с амплитудным значением, равным А. Вычислить автокорреляционную функцию импульса.

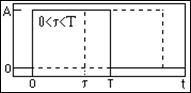При сдвиге копии импульса по оси t вправо, при 0≤t≤T сигналы перекрываются на интервале от t до Т. Скалярное произведение:

B_s(t) =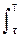A² dt = A²(T-t).

При сдвиге копии импульса влево, при -T≤t<0 сигналы перекрываются на интервале от 0 до Т-t. Скалярное произведение:

B_s(t) = 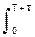A² dt = A²(T+t).

При |t| > T сигнал и его копия не имеют точек пересечения и скалярное произведение сигналов равно нулю (сигнал и его сдвинутая копия становятся ортогональными).

Обобщая вычисления, можем записать:

B_s(t) = .

В случае периодических сигналов АКФ вычисляется по одному периоду Т, с усреднением скалярного произведения и его сдвинутой копии в пределах периода:

B_s(t) = (1/Т)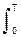s(t) s(t-t) dt.

При t=0 значение АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах интервала Т. АКФ периодических сигналов также является периодической функцией с тем же периодом Т. Для однотонального гармонического сигнала это очевидно. Первое максимальное значение АКФ будет соответствовать t=0. При сдвиге копии сигнала на четверть периода относительно оригинала подынтегральные функции становятся ортогональными друг другу (cos w_o(t-t) = cos (w_ot-p/2) º sin w_ot) и дают нулевое значение АКФ. При сдвиге на t=T/2 копия сигнала по направлению становится противоположной самому сигналу и скалярное произведение достигает минимального значения. При дальнейшем увеличении сдвига начинается обратный процесс увеличения значений скалярного произведения с пересечением нуля при t=3T/2 и повторением максимального значения при t=T=2p/w_o (cos w_ot-2p копии º cos w_ot сигнала). Аналогичный процесс имеет место и для периодических сигналов произвольной формы (рис. 2.11).

Рис. 2.11

Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ.

Для сигналов, заданных на определенном интервале [a, b], вычисление АКФ производится с нормировкой на длину интервала [a, b]:

B_s(t) =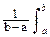s(t) s(t+t) dt. (2.26)

Автокорреляция сигнала может оцениваться и функцией автокорреляционных коэффициентов, вычисление которых производится по формуле (по центрированным сигналам):

r_s(t) = cos j(t) = ás(t), s(t+t)ñ /||s(t)||².

Взаимная корреляционная функция (ВКФ) сигналов (cross-correlation function, CCF) показывает как степень сходства формы двух сигналов, так и их взаимное расположение друг относительно друга по координате (независимой переменной), для чего используется та же формула (2.25), что и для АКФ, но под интегралом стоит произведение двух разных сигналов, один из которых сдвинут на время t:

B₁₂(t) = 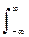s₁(t) s₂(t+t) dt. (2.27)

При замене переменной t = t-t в формуле (2.4.3), получаем:

B₁₂(t) =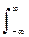s₁(t-t) s₂(t) dt =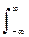s₂(t) s₁(t-t) dt = B₂₁(-t)

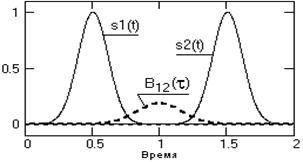
Рис. 2.12. Сигналы и ВКФ

Отсюда следует, что для ВКФ не выполняется условие четности, а значения ВКФ не обязаны иметь максимум при t = 0. Это можно наглядно видеть на рис. 2.12, где заданы два одинаковых сигнала с центрами на точках 0.5 и 1.5. Вычисление по формуле (2.27) с постепенным увеличением значений t означает последовательные сдвиги сигнала s2(t) влево по оси времени (для каждого значения s1(t) для подынтегрального умножения берутся значения s2(t+t)).

При t=0 сигналы ортогональны и значение B₁₂(t)=0. Максимум В₁₂(t) будет наблюдаться при сдвиге сигнала s2(t) влево на значение t=1, при котором происходит полное совмещение сигналов s1(t) и s2(t+t). При вычислении значений B₂₁(-t) аналогичный процесс выполняется последовательным сдвигом сигнала s1(t) вправо по временной оси с постепенным увеличением отрицательных значений t, а соответственно значения B₂₁(-t) являются зеркальным (относительно оси t=0) отображением значений B₁₂(t), и наоборот. На рис. 2.13 это можно видеть наглядно.

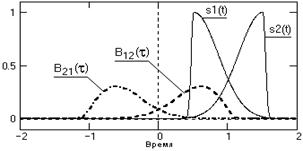
Рис. 2.13. Сигналы и ВКФ

Таким образом, для вычисления полной формы ВКФ числовая ось t должна включать отрицательные значения, а изменение знака t в формуле (2.27) равносильно перестановке сигналов.

Для периодических сигналов понятие ВКФ обычно не применяется, за исключением сигналов с одинаковым периодом, например, сигналов входа и выхода систем при изучении характеристик систем.

Функция коэффициентов взаимной корреляции двух сигналов вычисляется по формуле (по центрированным сигналам):

r_sv(t) = cos j(t) = ás(t), v(t+t)ñ /||s(t)|| ||v(t)||. (2.28)

Значение коэффициентов взаимной корреляции может изменяться от -1 до 1.

Дата добавления: 2014-01-03