Понятие собственных функций

Разложение сигналов по гармоническим функциям

Процедура анализа спектральным методом прохождения произвольного сигнала x(t) через произвольную линейную систему с импульсным откликом h(t) включает:

· определение спектральной функции X(w) ↔ x(t) входного сигнала с помощью прямого преобразования Фурье;

· определение комплексной передаточной характеристики H(w) ↔ h(t) линейной системы;

· определение спектральной функции сигнала Y(w) = X(w) H(w) на выходе системы;

· определение выходного сигнала y(t) ↔ Y(w) с помощью обратного преобразования Фурье.

Таким образом, анализ переходного процесса, вызываемого в системе входным сигналом, сводится к анализу стационарных решений воздействия на систему простых гармонических составляющих, каждая из которых действует от t = -∞ до ∞.

Помимо задач, связанных с анализом в системах переходных процессов, спектральными методами решаются также задачи синтеза систем, обладающих требуемой передаточной характеристикой и позволяющей получить на выходе сигнал заданной формы при определённом входном воздействии на систему.

Удобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных по координатам. Они проходят через линейные системы без изменения формы и частоты гармоники, изменяется только начальная фаза и амплитуда колебаний.

Допустим, что сигнал является линейной комбинацией функций синуса и косинуса:

s(х) = А sin(х)+B cos(х).

Сдвинем сигнал по аргументу на величину h. При этом получаем:

s(х+h) = C sin(х)+D cos(х),

C = А cos(h) – B sin(h), D = A sin(h) + B cos(h),

где коэффициенты C и D, как и в исходном выражении коэффициенты А и В, не зависят от аргумента, при этом C²+D² = А²+В². Таким образом, при произвольном переносе функции по аргументу (а равно и при интегрировании, дифференцировании и других линейных преобразованиях) любую линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций.

Экспоненциальная комплексная запись гармонических функций делает это свойство еще нагляднее. Для произвольной гармонической функции имеем:

cos(wt-j) = A cos(wt)+B sin(wt),

где A = cos(j), B = sin(j), j - начальный фазовый угол колебания при t = 0.

Переходя к комплексной записи данной функции с использованием тождеств Эйлера

cos(wt) = [ехр(jwt)+exp(-jwt)]/2, sin(wt) = [ехр(jwt)-exp(-jwt)]/2j,

получаем:

cos(wt-j) = C exp(jwt)+C*exp(-jwt),

где: C = 0,5 exp(-jj), C* = 0,5 exp(jj) – величина, комплексно сопряженная с С.

Применяя в качестве гармонической составляющей разложения сигнала функцию ехр(jwt), можно рассматривать вторую функцию ехр(-jwt), комплексно сопряженную с первой, как такую же составляющую, но с отрицательной частотой. Естественно, что отрицательная частота является математической абстракцией, но нужно помнить, что пара таких комплексно сопряженных составляющих в сумме всегда дает вещественную функцию, т.е. является отображением (образом) вещественной функции в новом математическом пространстве, базисом которого являются комплексные экспоненциальные функции.

Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса по аргументу:

exp[jw(t+h)] = exp(jwh)·exp(jwt) = H(w) exp(jwt),

где Н(w) = exp(jwh) - собственное значение операции переноса, независимое от переменной.

Для операции дифференцирования:

d[exp(jwt)]/dt = jw exp(jwt), H(w) = jw.

Для операции интегрирования:

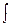exp(jwt) dt = (1/jw) exp(jwt), H(w) = 1/jw.

В общей форме, для любых линейных операций преобразования:

Т[exp(jwt)] = H(w) exp(jwt),

где T[.] - произвольный линейный оператор, H(w) - собственное значение операции, независимое от аргумента.

У специалистов-практиков существует предубеждение против использования комплексных функций с их мнимыми частотами. Поэтому в дальнейшем будем использовать и вещественные функции, и их комплексные аналоги, по крайней мере, до тех пор, пока простота и удобство использования последних не станет очевидным.

Дата добавления: 2014-01-03