АКФ периодических сигналов

Энергия периодических сигналов бесконечна, поэтому АКФ периодических сигналов вычисляется по одному периоду Т, с усреднением скалярного произведения сигнала и его сдвинутой копии в пределах периода:

B_s(t) = (1/Т)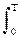s(t) s(t-t) dt. (6.5)

Математически более строгое выражение:

B_s(t) =.

При t=0 значение нормированной на период АКФ равно средней мощности сигналов в пределах периода. При этом АКФ периодических сигналов является периодической функцией с тем же периодом Т. Так, для сигнала
s(t) = A cos(w₀t+j₀) при T=2p/w₀ имеем:

B_s(t) =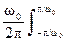A cos(w₀t+j₀) A cos(w₀(t-t)+j₀) = (A²/2) cos(w₀t). (6.6)

Полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств АКФ. С помощью функций автокорреляции можно проверять наличие периодических свойств в любых произвольных сигналах. Пример автокорреляционной функции периодического сигнала приведен на рис. 6.2.

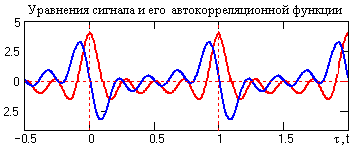
Рис. 6.2

Функции автоковариации (ФАК) вычисляются аналогично, по центрированным значениям сигнала. Замечательной особенностью этих функций являются их простые соотношения с дисперсией s_s² сигналов (квадратом стандарта – среднего квадратического отклонения значений сигнала от среднего значения). Как известно, значение дисперсии равно средней мощности сигналов, откуда следует:

|C_s(t)| ≤ s_s², C_s(0) = s_s² º ||s(t)||². (6.7)

Значения ФАК, нормированные на значение дисперсии, представляют собой функцию автокорреляционных коэффициентов:

r_s(t) = C_s(t)/C_s(0) = C_s(t)/s_s² º cos j(t). (6.8)

Иногда эту функцию называют "истинной" автокорреляционной функцией. В силу нормировки ее значения не зависят от единиц (масштаба) представления значений сигнала s(t) и характеризуют степень линейной связи между значениями сигнала в зависимости от величины сдвига t между отсчетами сигнала. Значения r_s(t) º cos j(t) могут изменяться от 1 (полная прямая корреляция отсчетов) до -1 (обратная корреляция).

На рис. 6.3 приведен пример сигналов s(k) и s1(k) = s(k)+шум с соответствующими этим сигналам коэффициентами ФАК - r_s и r_s1. Как видно на графиках, ФАК уверенно выявила наличие периодических колебаний в сигналах. Шум в сигнале s1(k) понизил амплитуду периодических колебаний без изменения периода. Это подтверждает график кривой C_s/s_s1, т.е. ФАК сигнала s(k) с нормировкой (для сопоставления) на значение дисперсии сигнала s1(k), где наглядно можно видеть, что шумовые импульсы при полной статистической независимости своих отсчетов вызвали увеличение значения С_s1(0) по отношению к значению C_s(0) и несколько "размыли" функцию коэффициентов автоковариации. Это вызвано тем, что значение r_s(t) шумовых сигналов стремится к 1 при t ® 0 и флюктуирует относительно нуля при t ≠ 0, при этом амплитуды флюктуаций статистически независимы и зависят от количества выборок сигнала (стремятся к нулю при увеличении количества отсчетов).

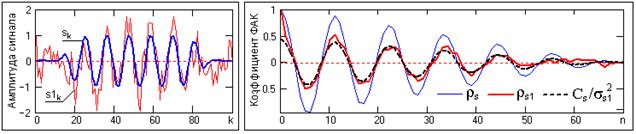
Рис. 6.3

Дата добавления: 2014-01-03