Спектр дискретного сигнала

Равномерная дискретизация

Допустим, что для обработки задается произвольный аналоговый сигнал s(t), имеющий конечный и достаточно компактный фурье-образ S(f). Равномерная дискретизация непрерывного сигнала s(t) с частотой F (шаг Dt = 1/F) с математических позиций означает умножение функции s(t) на гребневую функцию Ш_Dt(t) =d(t-kDt) – непрерывную последовательность импульсов Кронекера:

s_Dt(t) = s(t)×Ш_Dt(t) = s(t)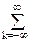d(t-kDt) =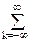s(kDt)d(t-kDt). (7.4)

С учетом известного преобразования Фурье гребневой функции

Ш_Dt(t) Û (1/T)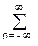d(f-nF) = F·Ш_F(f), (7.5)

фурье-образ дискретной функции s_Dt(t):

S_F(f) = S(f) _* F×Ш_F(f). (7.6)

Отсюда, для спектра дискретного сигнала имеем:

S_F(f) = F×S(f) _*d(f-nF) = FS(f-nF). (7.7)

Из выражения следует, что спектр дискретного сигнала представляет собой непрерывную периодическую функцию с периодом F, совпадающую (при определенных условиях конечности спектра непрерывного сигнала) с функцией F×S(f) непрерывного сигнала s(t) в пределах центрального периода от -f_N до f_N, где f_N = 1/2Dt = F/2. Частоту f_N (или для круговой частоты w_N = p/Dt) называют частотой Найквиста. Центральный период функции S_F(f) называют главным частотным диапазоном.

Интуитивно понятно, что если спектр главного частотного диапазона с точностью до постоянного множителя совпадает со спектром непрерывного сигнала, то по этому спектру может быть восстановлена не только форма дискретного сигнала, но и форма исходного непрерывного сигнала. При этом шаг дискретизации и соответствующее ему значение частоты Найквиста должны иметь определяющее значение.

Как правило, шаг дискретизации сигнала (шаг числовых массивов) условно принимают равным Dt = 1, при этом главный частотный диапазон занимает интервал -0.5 £ f £ 0.5, или, в шкале угловых частот, соответственно -p £ w £ p.

Физическая сущность формирования спектров дискретных сигналов достаточно проста. Наиболее наглядно это можно увидеть, если воспользоваться программой Mathcad (см. рис. 7.1).

Сначала представим себе непрерывный сигнал постоянной единичной амплитуды c(t) = const = 1 на произвольном интервале 0-Т, например, при Т=100. Начнем дискретизировать сигнал с равномерным шагом Dt=1. Вычислим спектр первого дискретного отсчета c₀ = 1. При N=1 сигнал является импульсом Кронекера, а, соответственно, модуль спектра отсчета с₀=1 представляет собой непрерывное частотное распределение |С(w)| = const в диапазоне от -¥ до +¥ (показан только участок от -6p до +6p с нормировкой на N для наглядности сравнения спектров). Все частоты сигнала имеют нулевую фазу и при сложении взаимно компенсируются во всех временных точках за исключением точки t=0, в которой амплитуды частот суммируются, создавая единичный отсчет с₀.

Рис. 7.1. Формирование спектра дискретного сигнала

Добавим к сигналу второй дискретный отсчет с₁=1 (N=2). Если вычислить спектр только второго отсчета, то его модуль будет равен модулю первого отсчета (так как с₁=с₀), но нулевые фазы гармоник этого спектра переместятся в точку t=1, т.е. относительно точки t=0 фазы гармоник второго отсчета изменятся на -wDt в соответствии с теоремой запаздывания преобразования Фурье. При сложении этих двух спектров первого и второго отсчета наблюдается интерференция частот и возникают пульсации частотного спектра с максимумами на частотах, кратных F=1/Dt или в угловых единицах 2p/Dt, где фазы спектров первого и второго отсчетов совпадают и равны нулю. Форма модуля результирующего спектра при N=2 приведена на рисунке.

При дальнейшем увеличении количества отсчетов периодичность совпадения нулевых фаз и положения максимумов сохраняется, а интерференция частот между максимумами усложняется, при этом ширина главных пиков по всему частотному диапазону спектра от минус до плюс бесконечности становится все уже. На рис. 7.1 приведены примеры спектров сигналов при N=10 и N=50. В пределе, при двусторонней временной шкале ±Т® ±¥ и N® ¥, гребневая функция из импульсов Кронекера во временной области c_t ® Ш_Dt(t) =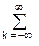d(t-kDt) превращается в идеальную гребневую функцию (1/T)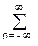d(f-nF) = F·Ш_F(f) в частотной области (формула 7.5). Этот спектр непрерывен и физически реален в диапазоне частот от -¥ до +¥.

Физический смысл интерференции частот остается тем же самым, если мы на произвольном интервале Т зададим произвольный сигнал, например – синусоиду u(t) Û U(f), и выполним его дискретизацию, т.е. умножим сигнал на непрерывную последовательность импульсов Кронекера c(t)×u(t) ® u(t)d(t-kDt) = u(t)× Ш_Dt(t). А так как каждый дискретный отсчет в этом случае имеет свою определенную амплитуду и, соответственно, свой уровень амплитуд гармоник своего спектра, то сложение частот дает более сложную картину интерференции с расщеплением спектра общего сигнала всех дискретных отсчетов на две зеркальных составляющих относительно кратных частот 2p/Dt.

Математически произведение двух функций во временной области отображается сверткой спектров этих функций в частотном представлении, т.е. сверткой спектра сигнала u(t) с частотной гребневой функцией спектра, порожденной временной гребневой функцией дискретизации u(t)Ш_Dt(t) Û U(f) _* F×Ш_F(f), откуда и следует формула (7.7). Пример дискретизации одного периода синусоиды приведен на рис. 7.2.

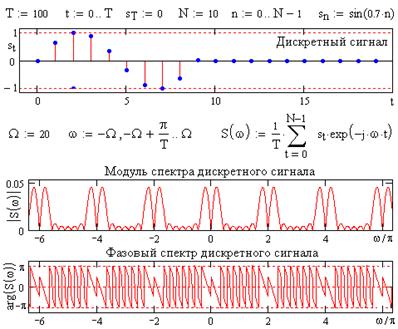
Рис. 7.2. Формирование спектра дискретного сигнала

Вернемся к значению и роли частоты Найквиста при дискретизации сигналов.

На рис. 7.3 и 7.4. приведены примеры равномерной дискретизации аналоговых сигналов s₁(t) = exp(-a|t|) и s₂(t) = exp(-bt²) (дискретные отсчеты нанесены кружками) и спектры этих дискретных сигналов.

Рис. 7.3. Дискретные сигналы Рис. 7.4. Спектры дискретных сигналов

Для того чтобы периодическое повторение спектра, вызванное дискретизацией аналогового сигнала, не изменяло спектр в главном частотном диапазоне (по отношению к спектру исходного аналогового сигнала), необходимо и достаточно, чтобы максимальные частотные составляющие f_max в спектре аналогового сигнала не превышали частоты Найквиста (f_max £ f_N = F/2). Это означает, что частота дискретизации сигнала должна быть минимум в два раза выше максимальной частотной составляющей в спектре сигнала:

F = 1/Dt ³ 2f_max, (7.8)

что обеспечивает выход спектра на нулевые значения на концах главного диапазона, как это имеет место для спектра S₂(w) на рис. 7.4.

Другими словами, на одном периоде колебаний с частотой f_max должно быть минимум две точки отсчета. Это и понятно – по одной точке отсчета на периоде гармонического сигнала определение неизвестных параметров данной гармоники (амплитуда, фаза) невозможно.

Если условие (7.8) нарушается, искажения частотного спектра исходного аналогового сигнала неизбежны. На рис. 7.4 наглядно видно, что частота дискретизации для сигнала s₁(t) данному условию не удовлетворяет, спектры периодов перекрылись, и результирующий спектр дискретных отсчетов сигнала s₁(t) отличается от фактического спектра сигнала (фактический спектр и его периодические повторения в области перекрытия спектра главного частотного диапазона со спектрами боковых диапазонов показаны пунктиром). Аналоговый сигнал из спектра S₁(w) будет восстановлен с искажениями.

Характер возникающих искажений во временной области при нарушении условия (7.8) можно наглядно видеть на рис. 7.5. На рисунке показаны три возможных варианта соотношения частот гармонических сигналов с постоянной частотой их дискретизации.

1. График А – частота гармонического сигнала меньше частоты Найквиста. Дискретным отсчетам может соответствовать только исходная гармоника, амплитуда, частота и фаза которой могут быть однозначно определены по любым трем последовательным точкам (три уравнения, три неизвестных).

2. График В – частота гармонического сигнала равна частоте Найквиста. Это означает периодическое повторение каждой пары последовательных отсчетов, а, следовательно, для решения имеется только два уравнения с тремя неизвестными с возможностью определения только частоты, и то при условии, что начальная фаза сигнала не совпадает с начальной фазой частоты дискретизации (в этом случае все отсчеты нулевые). Амплитуда и фаза сигнала определяются однозначно только при условии совпадения отсчетов с экстремумами гармоники.

Рис. 7.5. Дискретизация гармоник с разной частотой

3. График С – частота гармонического сигнала больше частоты Найквиста. Решение трех уравнений по трем последовательным точкам позволяет определить амплитуду гармоники, но дает искаженные значения частоты и фазы колебания (показано пунктиром). Это так называемый эффект появления ложных (кажущихся) частот (aliasing). Частоты гармонических колебаний выше частоты Найквиста как бы зеркально "отражаются" в главный частотный диапазон от его границ (на частоте Найквиста), что можно видеть на рис. 7.4 для действительного спектра сигнала S₁(w), показанного точками. Этот эффект аналогичен всем известному эффекту обратного вращения колес автомобиля (и любых других быстро вращающихся объектов) на экранах кино и телевизоров, когда скорость их вращения начинает превышать частоту смены кадров.

Дата добавления: 2014-01-03