Инверсии

Пример

Пример

Пример

Следующие примеры показывают приложение вышеупомянутых свойств.

1.

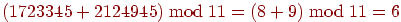
2.

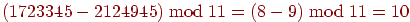
3.

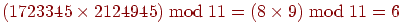
В арифметике мы часто должны находить остаток от степеней числа 10 при делении на целое число. Например, мы должны найти 10 mod 3, 10² mod 3, 10³ mod 3, и так далее. Мы также должны найти 10 mod 7, 10² mod 7, 10³ mod 7, и так далее. Третье свойство модульных операторов, упомянутое выше, делает жизнь намного проще.

10ⁿ mod x = (10 mod x)ⁿ Применение третьего свойства n раз.

Мы имеем

10 mod 3 = 1 10ⁿ mod 3 = (10 mod 3)ⁿ = 1

10 mod 9 = 1 10ⁿ mod 9 = (10 mod 9)ⁿ = 1

10 mod 7 = 3 10ⁿ mod 7 = (10 mod 7)ⁿ = 3ⁿ mod 7

Мы уже говорили, что в арифметике остаток от целого числа, разделенного на 3, такой же, как остаток от суммы деления его десятичных цифр. Другими словами, остаток от деления 6371 равен остатку от деления суммы его цифр (17), на 3. Мы можем доказать, что это утверждение использует свойства модульного оператора. Запишем целое число как сумму его цифр, умноженных на степени 10.

a = a_n10ⁿ +………+ a₁10¹ + a₀10⁰

Например: 6371 = 6 × 10³ + 3 × 10²+ 7 × 10¹+ 1 × 10⁰

Теперь мы можем применить модульную операцию к двум сторонам равенства и использовать результат предыдущего примера, где остаток 10ⁿ mod 3 равен 1.

a mod 3 = (a_n × 10ⁿ +……..+ a₁ × 10¹+ a₀ × 10⁰) mod 3

= (a_n × 10ⁿ) mod 3 +……..+ (a₁ × 10¹) mod 3 + (a₀ × 10⁰ mod 3) mod 3

= (a_n mod 3) × (10ⁿ mod 3) +……..+ (a₁ mod 3) × (10¹ mod 3) +

(a₀ mod 3) × (10⁰ mod 3) mod 3

= (a_n mod 3) +……..+ (a₁ mod 3) + (a₀ mod 3) mod 3

= (a_n +……..+ a₁ + a₀) mod 3

Когда мы работаем в модульной арифметике, нам часто нужно найти операцию, которая позволяет вычислить величину, обратную заданному числу. Мы обычно ищем аддитивную инверсию (оператор, обратный сложению) или мультипликативную инверсию (оператор, обратный умножению).

Дата добавления: 2014-01-03