Использование готовых оболочек (САМСТО) и программы DVIGwT для построения алгоритма решения и программы расчетов различных математических моделей

Статические и динамические математические модели; их особенности.

Иерархическая структура математических моделей сложных объектов; увязка уровней в иерархической сложной модели

Корректность моделей; оценка погрешности математического моделирования; устойчивость решения.

Корректность -точность(глубина) описания процессов в объекте моделирования

Математическая модель является корректной, если для нее осуществлен и получен положительный результат всех контрольных проверок размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, физического смысла и математической замкнутости.

Адекватность -способность ММ, отображать характеристики ТО с погрешностью не более заданной. Степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи. Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хо­рошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором — о сравне­нии с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требо­ваний, предъявляемых к модели, и ее назначения. При этом долж­на учитываться точность получения экспериментальных результа­тов или особенности постановок тестовых задач. В моделях, пред­назначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается точность 10-15%. В моделях, исполь­зуемых в управляющих и контролирующих системах, требуемая точность может быть 1-2% и даже более.

Как правило, различают качественное и количественное совпа­дение результатов сравнения. Фактически при каче­ственном сравнении оценивается совпадение лишь вида функции распределения параметров. Вопрос о количественном срав­нении можно ставить лишь после удовлетворительного ответа на вопрос о качественном соответствии результатов. При количествен­ном сравнении большое значение следует придавать точности ис­ходных данных для моделирования и соответствующих им значе­ний сравниваемых параметров

Оценка погрешностей производится по известным данным, которые известных из экспериментов или в сравнении с математической моделью более высокого уровня точности.

Устойчивость модели - это ее способность сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы.

Необходимо, чтобы производилась проверка на корректность исходных данных

При математическом моделировании достаточно сложного технического объекта (ТО) описать его поведение одной математической моделью, как правило, не удается, а если такая м.м. и была бы построена, то она оказалась бы слишком сложной для количественного анализа. Поэтому к таким моделям применяют принцип декомпозиции. Он состоит в условном разбиении ТО на отдельные более простые блоки и элементы, допускающие их независимое исследование с последующим учетом взаимного влияния блоков и элементов друг на друга. В свою очередь, принцип декомпозиции можно применить и к каждому выделенному блоку вплоть до уровня достаточно простых элементов. В таком случае возникает иерархия ММ связанных между собой блоков и элементов

Декомпозиция по каждой из ветвей древовидной структуры ведется до тех пор, пока не приведет к получению элементов системы, не требующих дальнейшего разложения

Рассмотрим иерархическую модель на примере ТЭЦ. Модель ТЭЦ относится к сложному ТО. Для создания такой модели необходимо применить иерархический подход.

ММ ТЭЦ будет состоять из ММ энергоблоков входящих в состав ТЭЦ, в свою очередь энергоблок можно разложить, к примеру на два главных объекта это котел и ПТ. И т.д.

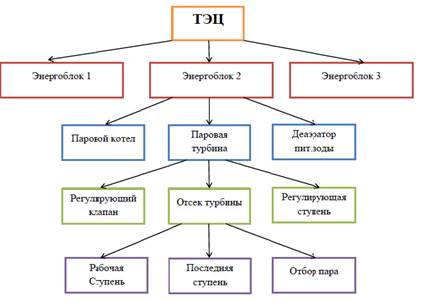
Рисунок 2-Иерархическая модель ТЭЦ

Все элементы должны быть увязан по целям моделирования,(к примеру для ММ ТЭЦ целью является определение тепловой эффективности, следовательно в элементе ПК должен определятся расход топлива и так далее спускаясь вниз по элементам).

Глубина описания процесса в каждом элементе должная быть на одном уровне одинакова. Уровни могут быть как вертикальными так и горизонтальными, Каждый элемен модели подчиняется вышестоящему.

По признаку учета зависимости объекта моделирования от времени различают статические и динамические характеристики систем, отражаемые в соответствующих моделях.

Статические модели (модели статики) отражают функцию системы - конкретное состояние реальной или проектируемой системы. Статические модели относятся к объектам, практически неизменяющимся во времени или рассматриваемым в отдельные временные сечения. Примеры. Закон Ома, описание показателей эффективности организацией в некоторый момент времени.

Динамические модели (модели динамики) отражают функционирование системы - процесс изменения состояний реальной или проектируемой системы. Они показывают различия между состояниями, последовательность смены состояний и развитие событий с течением времени. Динамические модели воспроизводят изменения состояний («движение») объекта с учетом как внешних, так и внутренних факторов. Примеры: описание процесса изменения показателей эффективности за некоторый период времени.

Для динамических моделей часто вводят понятия стационарность и нестационарность. Чаще всего стационарность выражается в неизменности во времени некоторых физических величин: стационарным является поток жидкости с постоянной скоростью, стационарна механическая система, в которой силы зависят только от координат и не зависят от времени.

Отличие статических и динамических моделей заключено в учете времени: в статике его как бы не существует, а в динамике это основной элемент.

В статических моделях 2 уровня модель описывается системой нелинейных уравнений, а в динамических моделях в свою очередь используются трансцендент­ных, дифференциальные уравнения.

В динамических моделях учитывается изменение накопления масс во объемах; иннерционность узлов; изменение теплового состояния деталей.

САМСТО предназначено для автоматизированного создания и развития систем моделирования и САПР в различных предметных областях. Это инструмент разработчика приложений, решающих задачи с использованием функциональной CAE-технологии. В САМСТО для моделирования авиационных двигателей применена концепция парапрограммирования (самопрограммирование).

С помощью САМСТО пользователь может добавлять в конкретные проекты новые типовые элементы, редактировать существующие и удалять ненужные.

Система DVIGwT создана в среде САМСТО и решает задачи структурного синтеза и параметрического анализа не только авиационных двигателей, но и энергетических установок произвольных схем.

Компьютерная среда DVIGwTпредназначена для выполнения термогазодинамических расчетов авиационных ГТД, наземных ГТУ, ПТУ, ПГУ, ТНУ произвольных схем и анализа их работы при изменении внешних условий и режимов работы. DVIGwТ позволяет изучать и анализировать работу как установки в целом, так и условия совместной работы отдельных ее узлов, например, компрессора, камеры сгорания, турбины и т.д. и элементов автоматики.

СистемаDVIGwТ основана на компонентной технологии построения модели установки. То есть с помощью декомпозитного подхода в распоряжении пользователя имеется набор типовых элементов, соответствующих узлам установки, из которых можно построить модель установки практически любой конструктивной схемы, включая гипотетические схемы. Расчет режимов работы производится в зависимости от нагрузки и климатических факторов, влияющих на работу установки на частичных режимах. Должны определяться и задаваться законы регулирования, обеспечивающие, к примеру, необходимую мощность установки за счет изменения расхода рабочего тела, при обеспечении постоянной частоты вращения роторов. В результате расчетов на номинальном и частичных режимах определяются показатели характерных точек тепловой схемы и общие показатели установки.

Расчетные задачи в контексте САМСТО/DVIGwТ представляют собой вложенные задачи САЕ, такие как структурный синтез- создание топологии модели пользователем; параметрический анализ- определение параметров двигателя в различных условиях; параметрический синтез- определение значений входных параметров; параметрическая оптимизация- нахождение оптимальных значений входных параметров в соответствии с заданной функцией цели; и структурная оптимизация- нахождение оптимальной схемы двигателя в соответствии с заданной функцией цели.

Дата добавления: 2014-01-03