Доверительные интервалы

Сводные характеристики выборки для партии материала.

Для исследователя важно знать точность и надежность оценки каждого определенного параметра, представления о которых дают доверительные интервалы.

Односторонним доверительным интервалом называют интервал от Х- ε до неизвестного параметра или от неизвестного параметра до Х+ ε, который устанавливает либо нижнюю, либо верхнюю границу неизвестного параметра с заданной доверительной вероятностью Р_д.

Двусторонним доверительным интервалом называют интервал от Х- ε до Х+ε, который покрывает неизвестный параметр распределения с заданной доверительной вероятностью Р_д.

Доверительная ошибка ε характеризует случайную ошибку параметра распределения. Чем меньше значение ε тем больше точность оценки Х.

Доверительной вероятностью Р_д или надежностью, соответствующей данному доверительному интервалу, называется вероятность того, что истинное значение многих числовых характеристик Х лежит в этом интервале.

Величина, равная a = 1 - Р_д называется уровнем значимости и иногда выражается в %. Она характеризует вероятность событий, условно принимаемые за невероятные.

Для контроля качества продукции доверительную вероятность Р_д принимают равной 0,95 – 0,99.

Доверительный интервал ограничен нижней и верхней доверительными границами, в его пределах с некоторой вероятностью находится сводная характеристика.

Доверительные интервалы для среднего значения.

Для односторонней границы:

Нижняя граница: 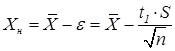(12)

Верхняя граница: 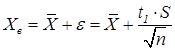(13)

Для двусторонних границ:

Нижняя граница: 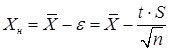(14)

Верхняя граница: 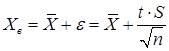(15)

где t₁ и t - квантили распределения Стьюдента при доверительной вероятности g = 0,95, значения которых приведены в таблице 5.

Таблица 5

K=n-1	t1	t	zн	zв	K =n-1	t1	t	zн	zв
	2,920	4,303	0,578	4,42		1,699	2,045	0,825	1,28
	2,353	3,182	0,620	2,92		1,684	2,021	0,847	1,23
	2,132	2,776	0,649	2,37		1,676	2,009	0,861	1,20
	1,833	2,262	0,729	1,65		1,660	1,984	0,897	1,13
	1,729	2,093	0,794	1,37	¥	1,645	1,960	1,000	1,00

В программе Excel доверительные интервалы рассчитываются с помощью функции ДОВЕРИТ (рис. 22). Она возвращает значение, с помощью которого можно определить доверительный интервал для математического ожидания генеральной совокупности. Доверительный интервал представляет собой диапазон значений. Выборочное среднее x является серединой этого диапазона, следовательно, доверительный интервал определяется как (x ± ДОВЕРИТ).

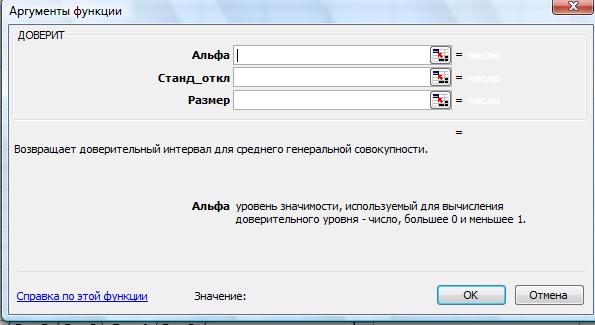
Рис. 22. Функция ДОВЕРИТ

ДОВЕРИТ (альфа; станд_откл; размер)

Альфа — это уровень значимости, используемый для вычисления уровня надежности. Уровень надежности равняется (1 - альфа)^.100%, или, другими словами, альфа равное 0,05 означает 95-процентный уровень надежности.

Станд_откл — это стандартное отклонение (среднее квадратическое отклонение) генеральной совокупности для интервала данных, оно предполагается известным.

Размер — это размер выборки.

Если какой-либо из аргументов не является числом, то функция ДОВЕРИТ возвращает значение ошибки #ЗНАЧ!.

Если альфа ≤ 0 или альфа ≥ 1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!

Если станд_откл ≤ 0, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Если размер не целое, то оно округляется.

Если размер < 1, то функция ДОВЕРИТ возвращает значение ошибки #ЧИСЛО!.

Доверительные интервалы для среднего квадратического отклонения.

определяются по следующим формулам, если число испытаний n<100:

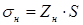(16)

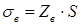(17)

где S – среднее квадратическое отклонение.

Значения Z_н и Z_в определяются с помощью табл.4.

При числе испытаний К=n-1 >100 значения Z_н и Z_в вычисляют по формулам:

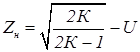(18)

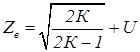(19)

где U = t₁ при n =∞ – квантиль распределения Стьюдента при доверительной вероятности Р_д=0,95.

Доверительные интервалы для коэффициента вариации.

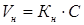(20)

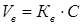(21)

где С – коэффициент вариации.

Значения К_н и К_в приведены в таблице 6.

Таблица 6

n
Kн	0,83	0,86	0,90	0,92	0,95	0,97
Kв	1,27	1,20	1,13	1,10	1,06	1,04

Дата добавления: 2014-01-03