Интегрирование данных

Интегрирование сигналов реализуется рекурсивными цифровыми фильтрами. Рассмотрим примеры анализа интегрирующих операторов.

Как известно, для точной операции интегрирования финитных сигналов в общем случае действительно преобразование:

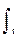s(t) dt «(1/jw) S(w).

Это выражение в правой части имеет особую точку при w = 0 и, соответственно, весовой дельта-импульс на нулевой частоте, пропорциональный постоянной составляющей сигнала. Оператор интегрирования в частотной области (1/jw) при w > 1 ослабляет в амплитудном спектре высокие частоты, а при 0 < w <1 усиливает низкие. Фазовый спектр сигнала смещается на -90⁰ для положительных частот и на 90⁰ для отрицательных.

Наиболее простыми и распространенными на практике алгоритмами интегрирования являются цифровые аналоги формул трапеций, прямоугольников и Симпсона.

Алгоритм интегрирования по формуле трапеций при нулевых начальных условиях:

y_k+1 = y_k+(s_k+1+s_k)/2. (4.2.1)

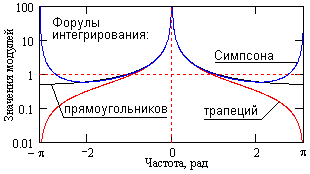Рис. 4.2.1. Частотные характеристики фильтров

Принимая s_k = exp(jwt) и y_k = H(w) exp(jwt), подставляем сигналы в (4.2.1) при t_k = kDt, Dt = 1 и решаем относительно H(w). Получаем:

H(w) = cos(w/2)/[2j sin(w/2)].

Частотная характеристика фильтра, а также фильтров интегрирования по другим формулам, приведена на рис. 4.2.1. В связи с накоплением результатов по всему предыдущему циклу суммирования и большим диапазоном значений модуля АЧХ характеристики фильтра более удобными, представительными и информационными являются частотные функции коэффициентов соответствия фактического интегрирования истинному:

K(w) = H(w)exp(jwt)/[(1/jw)exp(jwt)].

K(w) = cos(w/2)[(w/2)/sin(w/2)]. (4.2.2)

Графики коэффициентов соответствия всех фильтров интегрирования приведены на рис. 4.2.2

Оператор интегрирования по формуле прямоугольников (интерполяционное среднеточечное):

y_k+1 = y_k+s_k+1/2. (4.2.3)

После аналогичных подстановок сигнала и преобразований получаем:

K(w) = (w/2)/sin(w/2).

При численном интегрировании по формуле Симпсона уравнение фильтра имеет вид:

y_k+1 = y_k-1+(s_k+1+4s_k+s_k-1)/6. (4.2.4)

Частотный анализ фильтра проведите самостоятельно. Контроль:

K(w) = (2+cos w)/[3 sin(w)/w].

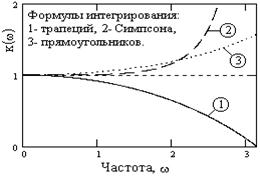Рис. 4.2.2. Коэффициенты соответствия.

Наиболее простые формулы цифрового интегрирования (трапеций и прямоугольников) ведут себя различным образом в главном частотном диапазоне. Формула прямоугольников завышает результаты на высоких частотах, а формула трапеций - занижает. Эти особенности легко объяснимы. Для одиночной гармоники площадь трапеции по двум последовательным отсчетам всегда меньше, чем площадь с выпуклой дугой гармоники между этими отсчетами, и разница тем больше, чем больше частота. В пределе, для гармоники с частотой Найквиста, отсчеты соответствуют знакочередующемуся ряду (типа 1, -1, 1, -1,... или любые другие значения в зависимости от амплитуды и начального фазового угла) и при нулевых начальных условиях суммирование двух последовательных отсчетов в формуле (4.2.1) будет давать 0 и накопления результатов не происходит. Интегрирование по площади прямоугольников с отчетом высоты по центральной точке между двумя отсчетами всегда ведет к завышению площади прямоугольника относительно площади, ограниченной выпуклой дугой гармоники.

Формула Симпсона отличается от формул трапеций и прямоугольников более высокой степенью касания единичного значения, что обеспечивает более высокую точность интегрирования в первой половине главного диапазона. Однако на высоких частотах погрешность начинает резко нарастать вплоть до выхода на бесконечность на конце диапазона (полюс в знаменателе передаточной функции рекурсивного фильтра на частоте Найквиста).

Эти особенности интегрирования следует учитывать при обработке данных сложного спектрального состава. Пример интегрирования сигнала и изменения его спектра приведен на рис. 4.2.3.

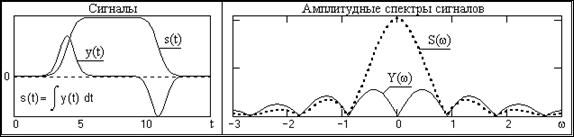
Рис. 4.2.3.

литература

Хемминг Р.В. Цифровые фильтры. – М.: Недра, 1987. – 221 с.

Дата добавления: 2014-01-03