Продолжение примера. 6. Вычисляем значения полюсов фильтра по формуле (10.1.10)

6. Вычисляем значения полюсов фильтра по формуле (10.1.10). Значения полюсов и их расположение на р-плоскости приведены на рис. 10.1.2. Положение первого полюса отмечено. Нумерация полюсов идет против часовой стрелки.

Как следует из формулы (10.1.10) и наглядно видно на рис. 10.1.2, все полюса с n ³ N являются комплексно сопряженными с полюсами n<N. Устойчивую минимально-фазовую передаточную функцию фильтра образуют полюса левой половины р-плоскости:

H(p) = G/B(p), (10.1.11)

где G - масштабный множитель, B(p) - полином Баттеруорта:

B(p) = B₁(p) B₂(p)... B_N(p), (10.1.12)

B_n(p) = p-p_n. (10.1.13)

Практическая реализация фильтра Баттеруорта при четном значении N производится в виде последовательной каскадной схемы биквадратными блоками, т.е. составными фильтрами второго порядка. Для этого множители B(p) в (10.1.12) объединяются попарно с обоих концов ряда по n (от 1 до N) по комплексно сопряженным полюсам, при этом для каждой пары получаем вещественные квадратичные множители:

В_m(p) = B_n(p)·B_N+1-n(p) =

= [p+j exp(jp(2n-1)/2N)][p+j exp(jp(2(N+1)-2n-1)/2N)] =

= [p+j exp(jp(2n-1)/2N)][p-j exp(jp(2n-1)/2N)] =

= p²+2p sin(p(2m-1)/2N)+1, n = 1,2,..., N/2; m = n. (10.1.14)

Общее количество секций фильтра M=N/2. При нечетном N к членам (10.1.14) добавляется один линейный множитель с вещественным полюсом p_(N+1)/2 = -1, пример положения которого на р-плоскости можно видеть на рисунке 10.1.2 для N=5:

В_(N+1)/2(p)= p+1. (10.1.15)

Машинное время фильтрации на один оператор фильтра первого или второго порядка практически не отличаются, поэтому использование операторов первого порядка можно не рекомендовать и при установлении порядка фильтра по формуле (10.1.6) округлять расчетное значение N в сторону большего четного числа, что создает определенный запас по крутизне среза частотной характеристики.

Таким образом, передаточная функция ФНЧ Баттеруорта в p-области при четном N:

H(p) = G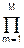1/B_m(p) = G 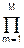1/(p²+a_mp+1), (10.1.16)

a_m = 2 sin(p(2m-1)/2N), m = 1,2,...,N/2. (10.1.17)

При нечетном N:

H(p) = (G/p+1)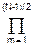1/(p²+a_mp+1), (10.1.16')

Дата добавления: 2014-01-03