Продолжение расчета

6'. Значения коэффициентов a_m и g_m (10.3.12), вычисленные по нормированным значениям s_n.

a_m = 0.067, 0.102, 0.198, 0.284, 0.317, 0.405, 0.407, 0.444.

g_m = 0.655, 1.527, 0.697, 1.436, 0.783, 1.277, 0.917, 1.091.

Коэффициент g билинейного преобразования для ненормированных значений w и полюсов s_n имеет классическую форму: g = 2/Dt. Соответственно, для нормированных значений: g = 2/(Dt·w_o). После билинейного z-преобразования выражения (10.3.11), получаем:

H(z) = G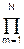G_m (1-z²)/(1-b_m z+c_m z²). (10.3.13)

G_m = 1/(g+a_m+g_mg^-1. (10.3.14)

b_m = 2G_m(g-g_mg^-1). (10.3.15)

c_m = G_m(g-a_m+g_mg^-1. (10.3.16)

Продолжение расчета (по нормированным полюсам s_n).

7. Значения коэффициента g: g = 1.363.

8. Значения G_m по (10.3.14): G_m = 0.523, 0.387, 0.483, 0.37, 0.444, 0.37, 0.409, 0.384.

9. Значения b_m по (10.3.15): b_m = 0.924, 0.188, 0.823, 0.23, 0.7, 0.315, 0.565, 0.432.

10. Значения c_m по (10.3.16): c_m = 0.93, 0.921, 0.809, 0.789, 0.719, 0.701, 0.666, 0.659.

11. Общий нормировочный множитель G: G = 1.264·10^-3.

12. Заключительная передаточная функция:

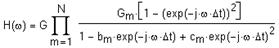
При построении графика данной функции можно убедиться, что она полностью соответствует рис. 10.3.2.

13. Уравнение одной секции фильтра:

y_m,k = G_m·(y_m-1,k - y_m-1,k-2) + b_m y_m,k-1 – c_m y_m,k-2 .

Нормировкой H(z) к 1 на геометрической средней частоте фильтра определяют общий множитель G:

G = 1/H(exp(-jDtw_o)). (10.3.17)

Если применить обратное частотное преобразование p = s(w_в-w_н)/(s²+w_в w_н), то в результате будет получен полосовой заградительный фильтр.

Дата добавления: 2014-01-03