Основы статистической группировки информации

При построении систем адаптивной фильтрации данных большое значение имеют статистические характеристики обрабатываемых сигналов и шумов, их стационарность, и наличие какой-либо дополнительной информации, коррелированной с основной. Возможность использования дополнительной информации при построении адаптивных систем рассмотрим на конкретном примере – системе адаптивной фильтрации данных непрерывных ядерногеофизических измерений.

Предпосылки метода. Физической величиной, регистрируемой в процессе ядерно-физических измерений в геофизике, обычно является частота импульсных сигналов на выходе детекторов ионизирующего излучения в интегральном или дифференциальном режиме амплитудной селекции. Значения измеряемой величины, как статистически распределенной по своей природе, могут быть определены только путем усреднения числа актов регистрации ионизирующих частиц по интервалам времени. Зарегистрированное количество импульсов определяет статистическую погрешность единичного измерения, а временной интервал усреднения, обеспечивающий нормативную погрешность – их производительность. Для методов с непрерывной регистрацией информации во времени (или в пространстве) временное окно измерений определяет также временную (или пространственную, с учетом скорости перемещения детектора) разрешающую способность интерпретации результатов измерений, при этом эффективность регистрации информации обычно ограничена условиями измерений и/или техническими средствами их исполнения. Типичный пример - каротаж скважин, где возможности увеличения интенсивности потоков информации ограничены параметрами эффективности регистрации и чувствительности детекторов излучения, которые зависят от их типа и размеров. Размеры детекторов, естественно, существенно зависят от размеров скважинных приборов, которые, в свою очередь, ограничены диаметрами скважин.

Ниже рассматривается возможность повышения точности и производительности непрерывных ядерно-физических измерений, для наглядности, применительно к условиям измерений в варианте скважинного гамма-опробования, хотя в такой же мере она может быть использована в авто- и аэрогаммасъемке, при радиометрическом обогащении руд, в рентгенорадиометрии и других методах ядерной геофизики. Предполагается, что регистрация данных производится в цифровой форме с накоплением отсчета по постоянным интервалам дискретизации данных (по времени и по пространству, при условии постоянной скорости перемещения детектора).

В общем случае полезная (целевая) информация может присутствовать в нескольких энергетических интервалах спектра излучения. Рабочими интервалами измерений обычно счи­таются участки спектра, где полезная информация присутствует в "чистом" виде либо в смеси с помехами (фоном), значение которых может быть учтено при обработке результатов изме­рений. Так, например, при гамма-опробовании пород на содержание естественных радионук­лидов (ЕРН) регистрируется излучение с энергией более 250-300 кэВ, представленное в основном первичными и однократно рассеянными квантами, плотность потока которых про­порциональна массовой доле ЕРН в породах. Плотность потока излучения в низкоэнергети­ческом интервале спектра (20-250 кэВ, в основном многократно рассеянное излучение) также зависит от массовой доли ЕРН, но эта зависимость является параметрически связанной с эф­фективным атомным номером излучающе-поглощающей среды в области детектора, вариации которого по стволу скважины могут приводить к большой погрешности интерпретации ре­зультатов измерений. Между тем плотность потока информации (относительно массовой доли ЕРН) в интервале 20-250 кэВ много выше, чем в интервале более 250 кэВ, осо­бенно при регистрации излучения сцинтилляционными детекторами малых объемов, которые имеют повышенную чувствительность именно к низкоэнергетической части спектра излуче­ния.

Задача статистической группировки информации в потоках сигналов в общей и наибо­лее простой форме может быть сформулирована следующим образом. Полезная информация присутствует в двух статистически независимых потоках сигналов (в двух неперекрывающихся интервалах спектра излучения). В первом потоке сигналов, условно- основном, полезная информация присутствует в "чистом" виде: плотность потока сигналов пропорциональна опреде­ляемой физической величине. Во втором потоке, условно-дополнительном, на полезную ин­формацию наложено влияние дестабилизирующих факторов, значение которых неизвестно. При отсутствии дестабилизирующих факторов коэффициент корреляции средних значений плотностей потоков в этих двух потоках сигналов постоянен и близок к 1. Для снижения ста­тистической погрешности измерений требуется осуществить извлечение полезной информа­ции из дополнительного потока сигналов и ее суммирование с основным потоком.

Обозначим потоки, а равно и частоты основного и дополнительного потоков сигналов индексами n и m (импульсов в секунду), связь потоков по частотам индексом х = m/n. Определению подлежит частота потока n. Значение х может изменяться за счет влияния дестабилизирующих факторов на поток m и в общем случае представляет собой случайную величину, распределенную по определенному закону с плотностью вероятностей Р(х), мате­матическим ожиданием 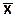, и дисперсией D_x.

На основе теоремы Байеса, плотность вероятностей распределения частоты n по измеренному за единичный интервал t числу отсчетов сигнала N определяется выражением:

P_N(n) = P(n) P_n(N) /P(N), (11.2.1)

P_n(N) = (nТ)^N e^-nt /N!, (11.2.2)

P(N) =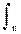P_n(N) P(n) dn, (11.2.3)

где: P(n) - априорная плотность вероятностей частоты n, P_n(N) - апостериорное распределе­ние вероятностей числовых отсчетов N (закон Пуассона). Принимая в дальнейшем в качестве искомой величины значения отсчетов z=nt по интервалам t (экспозиция цифровых отсчетов или скользящее временное окно аналоговых данных) и подставляя (11.2.2, 11.2.3) в (11.2.1), получаем:

P_N(z) = P(z) z^N e^-z /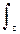P(z) z^N e^-z dz. (11.2.4)

При неизвестном распределении значений z априорная плотность распределения P(z) принимается равномерной от 0 до ¥, при этом из выражения (11.2.4) следуют общеизвестные выражения:

z = D_z = N+1 @ N, (11.2.5)

d_z² = D_z /z² = 1 /(N+1) @ 1/N. (11.2.6)

Значениями единиц в выражениях пренебрегаем, что не только корректно в условиях "хорошей" статистики, но и необходимо в режиме последовательных непрерывных измерений для исключения смещения средних значений.

Как следует из теории гамма-каротажа (ГК) и достаточно хорошо подтверждено практикой гамма-опробования, пространственная разрешающая способность гамма-каротажных измерений при интерпретации результатов ГК на содержание естественных радиоактивных элементов в породах по стволу скважин в среднем составляет 10 см, а в скважинах малого диаметра может даже повышаться до 5-7 см. Однако реализация такой разрешающей способности возможна только в условиях достаточно "хорошей" статистики. Коэффициент усиления дисперсии помех цифровых фильтров деконволюции, которые используются при интерпретации ГК, в среднем порядка 12 и изменяется от 4 до 25 в зависимости от плотности пород, диаметра скважин, диаметра скважинных приборов и пр. Отсюда следует, что для достижения разрешающей способности в 10 см при нормативной погрешности дифференциальной интерпретации не более 10-20 % статистическая погрешность измерений не должна превышать 3-7 %. А это, в свою очередь, определяет объем отсчета за единичную экспозицию не менее 200-1000 импульсов. При гамма-каротаже последнее возможно только для пород с относительно высоким содержанием ЕРН (более 0.001 % эквивалентного урана), при использовании детекторов больших размеров (с эффективностью регистрации более 10 имп/сек на 1 мкР/час) и при низкой скорости каротажа (не более 100-300 м/час). В той или иной мере эта проблема характерна для всех методов ядерной геофизики, и особенно остро стоить в спектрометрических модификациях измерений.

Вместе с тем следует отметить, что процесс непрерывных измерений имеет определенную физическую базу как для применения методов регуляризации результатов интерпретации данных, так и для регуляризации непосредственно самих статистических данных (массивов отсчетов N) при их обработке.

Простейшим способом подготовки цифровых данных для интерпретации является их низкочастотная фильтрация методом наименьших квадратов (МНК) или весовыми функциями (Лапласа-Гаусса, Кайзера-Бесселя и др.). Однако любые методы низкочастотной фильтрации данных снижают пространственную разрешающую способность интерпретации, так как кроме снижения статистических флюктуаций приводят к определенной деформации частотных составляющих полезной части сигнала, спектр которого по условиям деконволюции должен иметь вещественные значения вплоть до частоты Найквиста. В определенной мере ликвидировать этот негативный фактор позволяет метод адаптивной регуляризации данных (АРД).

Выражения (11.2.5-6) получены в предположении полной неизвестности априорного распределения P(z)для отсчетов в каждой текущей экспозиции t. Между тем, при обработке данных непрерывных измерений, и тем более каротажных данных, которые обычно являются многопараметровыми, для каждого текущего отсчета при обработке данных может проводиться определенная оценка распределения P(z). Как минимум, можно выделить два способа оценки распределения P(z).

Способ 1. По массивам данных параллельных измерений каких-либо других информационных параметров, значения которых достаточно четко коррелированны с обрабатываемым массивом данных либо в целом по пространству измерений, либо в определенном скользящем интервале сравнения данных. К таким массивам относятся, например, предварительные каротажные измерения в процессе бурения скважин, измерения другим прибором, с другой скоростью каротажа, в другом спектральном интервале излучения, и даже другим методом каротажа. При гамма-опробовании оценка распределения P(z) может производиться по параллельным измерениям интенсивности потока m в низкочастотном интервале спектра горных пород.

Способ 2. При единичной диаграмме ГК оценка распределения P(z) в каждой текущей точке обработки данных может выполняться по ближайшим окрестностям данной точки, захватывающим более широкий пространственный интервал по сравнению с интервалом отсчетов.

Использование априорных данных. Допустим, что кроме основного массива данных N, подлежащего обработке (подготовке к интерпретации), мы располагаем дополнительным массивом данных M, значения которого в определенной степени коррелированы с массивом N. При отсутствии дополнительных массивов способ 2 позволяет получить массив М обработкой массива N цифровым фильтром МНК (или любым другим весовым фильтром) со скользящим временным окном T ³ 3t (M(k) = m(k)tсглаженного сигнала m(k) = n(k) ③ h, где h – оператор симметричного цифрового фильтра). Отметим также, что 2-ой способ всегда может использоваться для регуляризации данных независимо от наличия данных для 1-го метода.

Массив М позволяют дать оценку статистических характеристик распределения P(z). Так, если для тех же интервалов времени t в массиве М имеются отсчеты М = m_kt (или приведенные к ним отсчеты какого-либо другого параметра), то можно записать:

P_M(z) =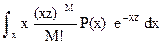, (11.2.7)

где Р(х) – априорная плотность распределения значений x_k = m_k/n_k, которые в общем случае также могут быть случайными. При равномерном распределении Р(х) от 0 до ¥ для отсчета М равновероятно любое значение z, т.е. эффект от измерений в потоке m отсутствует. Однако по исходным условиям задачи в потоке m обязательно присутствие полезной информации, а, следовательно, и суще­ствование, как минимум, определенных границ распределения Р(х) от х_min > 0 до x_max << ¥, и среднего значения 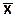по пространству измерений. При этом из выражения (11.2.7) следует, что наиболее вероятное значение z_a, "априорное" для отсчетов z=nt в потоке n по измерениям в потоке m (отсчетам М), должно быть равно:

z_a = (M+1)/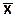@ М/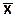. (11.2.8)

При статистической независимости величин х и М относительная средняя квадратическая погрешность определения значений z_a по отсчетам в массиве М:

d_za² = d_M² + d_x². (11.2.9)

Отсюда дисперсия распределения значений z_a:

D_za = (D_M+M²d_x²)/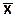² = D(M) /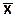², (11.2.10)

D(M) = D_M+M²d_x² = D_M+D_xm , (11.2.11)

D_M = М+1 @ М, D_xm = M²d_x²,

где значение дисперсии D_M определяется статистикой отсчетов в массиве М при х = const, значение D_xm представляет собой дисперсию значений М за счет флюктуаций величины х, а сумма D(M) определяет полную дисперсию отсчетов М.

Влияние Р(х) на форму распределения Р_М(z) сказывается в его "растягивании" по координате z относительно модального значения, при этом решение интеграла (11.2.7) в первом приближении может быть представлено в следующем виде:

P_M(z) @ b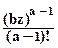e^-bz. (11.2.12)

Для данного распределения:

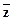= z_a = a/b, (11.2.13)

D_za = a/b², (11.2.14)

С учетом выражений (11.2.8) и (11.2.10):

a = MD_M/(D_za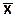²) = MD_M/D(M), (11.2.15)

b = D_M/(D_za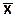) = 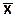D_М/D(M). (11.2.16)

Значение 'а' в выражении (11.2.15) принимается целочисленным. Выражение (11.2.12) может быть принято для распределения (11.2.4) в качестве априорного распределения вероятностей Р(z), при этом:

P_N(z) = (b+1)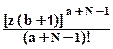e^-z(b+1). (11.2.17)

Отсюда, математическое ожидание и дисперсия z:

z = (N+a)/(b+1), (11.2.18)

D_z = (N+a)/(b+1)². (11.2.19)

C использованием выражений (11.2.15-16):

z = bN+(1-b)M/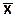, (11.2.20)

где b и (1-b) – весовые коэффициенты доверия отсчетам N и M:

b = D(M)/(D_N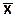²+D(M)). (11.2.21)

Дисперсия и относительная средняя квадратическая погрешность отсчетов z:

D_z = D(M)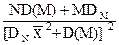, (11.2.22)

d_z² =1/(N+MD_M/D(M)). (11.2.23)

Эффективность метода. Сравнение выражений (11.2.20-23) и (11.2.5-6) позволяет дать оценку эффекта использования дополнительной информации из статистически независимого от N потока М (произвольная дополнительная информация).

1. При 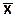Þ const имеет место d_х² Þ 0, D_xm Þ 0 и дисперсия отсчетов в массиве М определяется только статистикой потока:

D(M) Þ D_M = M, z = (N+M) /(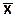+1),

d_z² Þ 1/(N+M) < d_N² = 1/N, (11.2.24)

h = d_N² /d_z² = [N+M²/D(M)] /N Þ 1+M/N,

что соответствует определению z по двум независимым измерениям и эффект использования дополнительной информации максимален. Так, при M» N, h Þ 2 и погрешность измерений уменьшается в 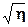~1.4 раза.

2. В общем случае D_xm ¹ 0, при этом D(M) > D_М и положительный эффект снижается. В пределе: d_x Þ ¥, D_xm Þ ¥, D(M) Þ ¥, h Þ 1, z Þ N, d_z Þ d_N и положительный эффект полностью вырождается. Во всех остальных случаях h > 1 и d_z < d_N. Отсюда следует, что при наличии коррелированной информации в массиве М положительный эффект, в той или иной мере, всегда имеет место.

3. Положительный эффект тем больше, чем больше значение x = m/n, меньше флюктуации х (величина d_х), и меньше значения отсчетов N = nt. Положительный эффект увеличивается именно в тех случаях, когда особенно остро ощущается недостаток информации: при малых значениях плотности потока излучения и/или экспозиции измерений.

Аналогичный эффект будет иметь место и при формировании отсчетов M по окрестностям текущих точек обработки данных путем определения их среднего значения (низкочастотное сглаживание массива n). Предварительное низкочастотное сглаживание может применяться и для статистически независимого дополнительного массива m, что будет повышать достоверность прогнозных отсчетов и увеличивать глубину регуляризации, если это сглаживание при регуляризации по формулам (11.2.20 и 21) не сказывается на изменении формы основного сигнала. Последнее определяется соотношением частотных спектров основного сигнала и оператора сглаживания.

Возможны два способа реализации уравнения (11.2.20): непосредственно в процессе измерений методом статистической группировки полезной информации (СГПИ) в реальном масштабе времени, или методом статистической регуляризации данных (СРД), зарегистрированных в виде временного (пространственного) распределения в параллельных массивах отсчетов.

Дата добавления: 2014-01-03