Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события

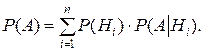
Данная формула является следствием из обеих теорем – теорем сложения и умножения вероятностей.

При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства

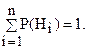
Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.

Таким образом оказывается, что знания вероятностей гипотез Р(Н₁), Р(Н₂), Р(Н₃), о возможных исходах стрельбы и условных вероятностей наступления интересующего нас события А – поражение танка при осуществлении этих гипотез Р(А|Н₁), Р(А|Н₂), Р(А|Н₃) является достаточным для вычисления вероятности поражения танка, т.е. наступления интересующего нас события А.

Вернёмся к решению примера.

Решение:

Таким образом, возможные гипотезы об исходах стрельбы:

Н₁ = {попадание в башню танка};

Н₂ = {попадание в корпус танка};

Н₃ = {попадание в ходовую часть}.

По условию задачи вероятности гипотез будут равны:

гипотеза Н₁={попадания в башню танка} – равна 0,2 (Р(Н₁) = 0,2);

гипотеза Н₂ ={попадание в корпус танка} – равна 0,3 (Р(Н₂) = 0,3);

гипотеза Н₃ ={попадание в ходовую часть} – равна 0,1 (Р(Н₃) = 0,1).

Интересующее нас событие А = {поражение танка}. По условию задачи вероятность поражения танка при реализации гипотез:

Н₁ = {попадание в башню танка} равна 0,8 (Р(А|Н₁) = 0,8);

Н₂ = {попадание в корпус танка} равна 0,6 (Р(А|Н₂) = 0,6);

Н₃ = {попадание в ходовую часть} равна 0,5 (Р(А|Н₃) = 0,5).

Проверим, все ли гипотезы об исходах стрельбы учтены:

Р(Н₁) + Р(Н₂) + Р(Н₃) = 0,2 + 0,3 + 0,1 = 0,6 ¹1.

Следовательно, имеющиеся гипотезы не составляют полной группы событий и не учтено событие Н₀={промах}, вероятность которого можно определить как вероятность противоположного попаданию в танк события – промаху – :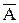

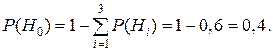
Таким образом, вероятность гипотезы Н₀ ={промах} равна 0,4. (Р|Н₀) =0,4).

Вероятность поражения танка при реализации гипотезы Н₀={промах} равна 0. (Р(А|Н₀) = 0).

Применяя формулу полной вероятности для решения задачи получим:

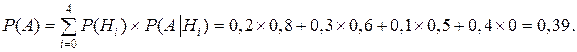
Следовательно, полная вероятность поражения танка при одном выстреле равна

Р(А) = 0,39 = 39%.

Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.

Заключительная часть занятия:

· напомнить тему и учебные вопросы занятия;

· отметить степень достижения учебных целей;

· ответить на возникшие вопросы;

· отметить работу группы в целом;

· оценить работу студентов;

· поставить задачу на подготовку к следующему занятию:

На занятии иметь:

Калькуляторы – на каждого

Задание на самостоятельную работу

Изучить:

· Вентцель Е.С., Овчаров Л.А.. Теория вероятностей и её инженерные приложения. Учебное пособие. Издание третье, переработанное и дополненное. – М.: «Академия», 2003 г. – 464 с. – стр. 32-35

· Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. – М.: Высшая школа», 2004 г. – 480 с. – стр.18-29.

Дата добавления: 2014-01-03