Величина, значения которой от испытания к испытанию изменяются случайным образом, называется случайной величиной

Случайные величины принято обозначать прописными буквами Х; У; Z …, а возможные частные значения, которые может принять случайная величина, - соответственно строчными буквами х₁, х₂,…х_n…; у₁, у₂,…у_i,…, у_n.

Если не указывается, какое именно из возможных значений принимает случайная величина, её могут обозначать как х; y.

Понятие случайной величины является фундаментальным понятием теории вероятностей и играет большую роль в её приложениях. Введение понятия случайной величины значительно расширило возможности теории вероятностей при исследовании случайных явлений. Заслуга широкого внедрения в теорию вероятностей понятия «случайная величина» принадлежит русскому учёному П.Л. Чебышеву.

Приведём ряд примеров случайных величин.

Пример 1: По цели производится 3 выстрела. Число попаданий в цель при трёх выстрелах является случайным.

Случайная величина Х = {число попаданий в цель при трёх выстрелах}.

Случайная величина Х = {число попаданий в цель при трёх выстрелах} в результате опыта может принять следующие частные значения: х₁ = 0; х₂ = 1; х₃ = 2; х₄ = 3.

Эти частные значения случайной величины (рисунок 1) могут быть расположены на числовой оси изолированно, причём в определенной последовательности (пронумерованы), и могут быть определены до опыта.

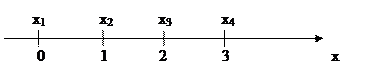
Рисунок 1

Пример 2: Стрельба по цели ведётся до первого попадания. Число снарядов, необходимых для получения попадания в цель является случайным.

Случайная величина Y = {число снарядов, необходимых для получения одного попадания}.

Случайная величина Y = {число снарядов, необходимых для получения одного попадания} в результате опыта может принять следующие частные значения:

y₁ = 1; y₂ = 2; y₃ = 3;…y_k = k; y_k+1 = k+1…¥

Возможные частные значения случайной величины Y = {число снарядов, необходимых для получения одного попадания} (рисунок 2) также как и в первом примере могут быть расположены на числовой оси в определенной последовательности изолированно, и могут быть определены до опыта.

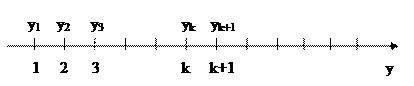
Рисунок 2

Однако в отличие от случайной величины Х, возможных значений случайной величины Y бесконечно много (но при этом счётно, так как их можно пересчитать).

Пример 3: Производится несколько выстрелов из орудия. Отклонение точек падения снарядов от центра рассеивания снарядов случайно.

Случайная величина Х={удаление точки падения снаряда от центра рассеивания снарядов}.

Рассеивание снарядов неравномерно, симметрично и небеспредельно.

Таким образом, снаряд может упасть в любую точку интервала, ограниченного пределами технического рассеивания снарядов от -4В¶ до +4В¶.

Следовательно, все числа из этого интервала будут возможными значениями случайной величины Х = {удаления точки падения снарядов от центра рассеивания снарядов (ЦРС)}.

Характерной особенностью данной случайной величины Х (рисунок 3) является то, что перечислить все ее частные значения (или все точки интервала числовой оси) не представляется возможным, т.к. их число бесконечно и несчетно. Для подобной случайной величины Х можно указать лишь границы, в которых она может появиться.

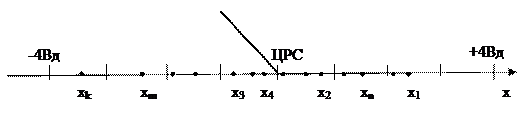
Рисунок 3

Из приведенных выше примеров мы видим, что случайные величины могут принимать как отдельные (счётные), имеющие конечное или бесконечное множество значений (примеры 1,2), так и непрерывно заполнять некоторый промежуток числовой оси (иметь несчётное множество возможных значений) (пример 3).

Исходя из этого, различают следующие типы случайных величин: дискретные (прерывные) и непрерывные.

Дискретная (прерывная) случайная величина – это такая случайная величина, которая в результате испытаний может принимать только отдельные изолированные значения.

Характерными особенностями дискретной случайной величины являются:

1. возможные значения дискретной случайной величины на числовой оси располагаются изолированно;

2. число возможных значений дискретной случайной величины может быть как конечно так и бесконечно, но оно всегда счётно;

3. возможные значения дискретной случайной величины могут быть перечислены заранее до опыта.

Непрерывная случайная величина – это такая случайная величина, которая в результате испытания может принимать любое значения из бесчисленного множества значений некоторого промежутка.

Характерными особенностями непрерывной случайной величины являются:

1. возможные значения непрерывной случайной величины непрерывно заполняют некоторый промежуток числовой оси;

2. возможные значения непрерывной случайной величины нельзя расположить в определенной последовательности (пересчитать), их бесчисленное множество;

3. возможные значения непрерывной случайной величины нельзя перечислить до опыта, возможно указать лишь границы промежутка, в которых она может появиться.

В результате опыта случайная величина может принимать то или иное частное значение. Очевидно, что знание возможных значений случайной величины х₁, х ₂, … х_n ещё не позволяет полностью описать случайную величину X. Необходимо ответить на вопрос – как часто в результате повторения опыта в одних и тех же условиях следует ожидать появления тех или иных возможных значений случайной величины. Другими словами, какова вероятность появления различных частных значений случайной величины. Причём, для дискретных случайных величин имеется возможность установить ряд этих значений, а для непрерывных – промежутки этих значений.

Вернёмся к примеру 1. Так как несовместные события х₁,=0, х₂=1, х₃=2, х₄=3 образуют полную группу, то должно выполняться условие:

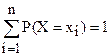
Очевидно, что эта суммарная вероятность каким-то образом распределена между отдельными значениями случайной величины .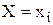

С вероятностной точки зрения дискретная случайная величина Х будет полностью описана в том случае, если мы в точности укажем, какой вероятностью обладает каждое из событи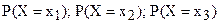й: и 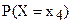, а для случайной непрерывной величины вероятность того, что случайная величина примет значение некоторого промежутка числовой оси - .

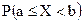Таким образом, вводится новое, очень важное понятие теории вероятностей – закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными частными значениями случайной величины и соответствующими им вероятностями.

Про случайную величину в этом случае говорят, что она подчинена данному закону распределения.

Закон распределения является исчерпывающей вероятностной характеристикой случайной величины, полностью описывающий с вероятностной точки зрения поведение случайной величины.

2. Формы закона распределения случайной величины: ряд распределения, функция распределения, функция плотности распределения

Способы или формы представления закона распределения случайной величины могут быть различны.

Наиболее просто решается задача вероятностной оценки для дискретной случайной величины. Для этого достаточно указать, какой вероятностью обладает каждое из событий х₁, х₂, х₃, … х_n: Р(Х = х₁) = р₁; Р(Х = х₂) = р₂; Р(Х = х₃) = р₃; Р(Х = х_n) = р_n.

Рассмотрим дискретную случайную величину Х = {число попаданий при 3 выстрелах}.

Пусть вероятность попадания в цель равна 0,3 и от выстрела к выстрелу не изменяется.

Возможные частные значения случайной величины Х = {число попаданий при 3 выстрелах} могут быть следующими: ни одного попадания – х₁ = 0; одно попадание – х₂ = 1; два попадания – х₃ = 2; все три попадания – х₄ = 3.

Вероятности частных значений случайной величины найдём по формуле Бернулли:

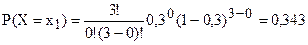
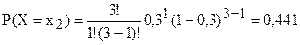
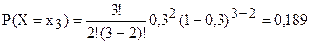
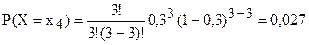
Проведём проверку учета всех гипотез:

0,343 + 0,441 + 0,189 + 0,027 = 1

Таким образом, мы определили вероятность наступления каждого из всех несовместных событий и с вероятностной точки зрения полностью охарактеризовали случайную величину Х = {число попаданий при 3 выстрелах}, поставив в соответствие каждому частному значению случайной величины х₁ = 0; х₂ = 1; х₃ = 2; х₄ = 3 вероятность его появления: 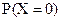=0,343, 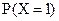=0,441, 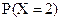=0,189, 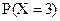=0,027.

Такая форма закона распределения дискретной случайной величины называется рядом распределения.

Закон распределения дискретной случайной величины, когда каждому частному значению х₁, х₂, х₃, … х_n случайной величины Х ставится в соответствие её вероятность:

Р(Х = х₁) = р₁; Р(Х = х₂) = р₂; Р(Х = х₃) = р₃; Р(Х = х_n) = р_n.

называется рядом распределения дискретной случайной величины.

Ряд распределения, как правило, представляют в виде таблицы, где в верхней строке в порядке возрастания размещают возможные частные значения случайных величин, а в нижней – соответствующие им вероятности.

хi
Р(Х = хi)	0,343	0,441	0,189	0,027

При составлении ряда распределения следует иметь в виду, что все события являются несовместными, т.к. случайная величина Х может принять в результате испытания только одно значение. Эти события случайны, т.к. нельзя указать, какое значение примет случайная величина и, последнее, все события должны образовывать полную группу событий, т.к. никаких других событий, кроме перечисленных, в результате опыта произойти не может.

На основании вышеизложенного, что события Х = х_i (i = 1, 2, 3, … n) образуют полную группу несовместных событий, сумма вероятностей всех возможных частных значений должна удовлетворять условию:

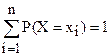
Ряд распределения можно представить графически, для этого по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – вероятности этих значений (рисунок 4).

1

0,4

0,441

0,3

	0,189

0,343

0,2

0,1

0 х

1 2 3

Рисунок 4

Для наглядности вершины полученных ординат соединяют пунктирными отрезками. Следует помнить, что соединение вершин прямыми делается только в целях наглядности, т.к. в промежутках между х₁ и х₂; х₂ и х₃ и т.д., дискретная случайная величина Х значений принять не может, следовательно, вероятность ее появления в этих промежутках равна 0. Полученную фигуру называют многоугольником распределения.

Рассмотренный ряд распределения является весьма удобной формой представления закона распределения. Однако основным недостатком данной формы закона распределения является то, что область его применения ограничивается распределением дискретной случайной величины с конечным числом возможных значений.

Для непрерывной случайной величины, когда возможные значения случайной величины заполняют всю числовую ось или какой-то ее интервал, поставить в соответствие каждому частному значению случайной величины соответствующую ему вероятность, невозможно. Множество возможных значений такой случайной величины несчетно (их невозможно перечислить в верхней части таблицы). Это вызывает необходимость иметь такую форму представления закона распределения, которая была бы приемлема не только для вероятностной характеристики дискретной случайной величины, но и для непрерывной, когда необходимо определить вероятность появления случайной величины на некотором промежутке числовой оси.

То есть, иметь какую то универсальную форму закона распределения для всех типов случайной величины.

Для количественной характеристики распределения как дискретной, так и непрерывной случайной величины, удобно воспользоваться не вероятностью события Х = х_i, а вероятностью события Х < х, где х – некоторая текущая переменная. Вероятность такого события есть некоторая функция от х – F(x). Эта функция носит название функции распределения случайной величины Х.

Функцией распределения случайной величины Х называется функция аргумента х, равная вероятности того, что случайная величина примет любое значение, меньше чем х.

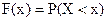
На примере дискретной случайной величины Х = {число попаданий при 3 выстрелах} покажем, как возможно составить фикцию распределения. (Однако здесь необходимо несколько абстрагироваться от того, что число попаданий может быть только натуральными числами: 0, 1, 2, 3, но и иметь дробное значение, а также меньше 0 и больше 3, т.е. рассмотреть все возможные значения числовой оси).

Рассчитаем функцию распределения дискретной случайной величины Х = {число попаданий при 3 выстрелах}:

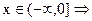
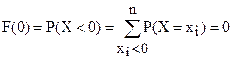, событие невозможное

,

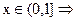
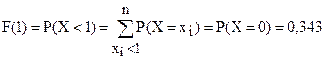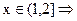
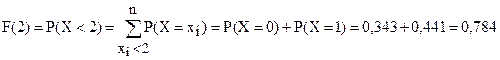
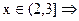
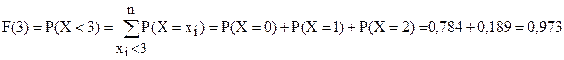
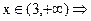
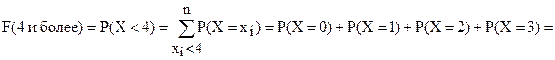
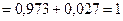
Таким образом, функция распределения случайной величины Х= {число попаданий при 3 выстрелах} будет иметь следующий вид:

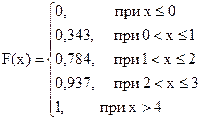
Отобразим полученную функцию распределения F(x) в виде графика (рисунок 5):

F(х)

1

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0.2

0,1

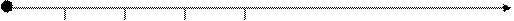
х

0 1 2 3 4

Рисунок 5

Функция распределения дискретной случайной величины являетсяступенчатой функцией.

Из графика функции распределения (рис. 5) видно, что в возможных частных значениях дискретной случайной величины Х функция разрывается и поднимается скачками на величину вероятности соответствующего значения случайной величины.

Значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси Ох.

Сумма всех скачков функции F(x) равна 1 (в соответствии с условием:

).

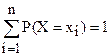По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки – меньше, ступенчатая кривая становится более плавной, дискретная случайная величина постепенно приближается к непрерывной, а ее функция распределения – к непрерывной функции.

В принципе, любую непрерывную величину можно рассматривать как дискретную. Ведь измеряя какое-то ее значение по результатам опыта, например, удаление точки падения снаряда от цели, мы всегда выражаем ее в каких-то единицах измерения (метрах, сантиметрах). В реальности такая замена не всегда оправдана так как, во-первых, всегда имеется потенциальная возможность повысить точность измерения, а во-вторых, частные значения случайной величины могут быть очень тесно расположены на числовой оси. В этих случаях проще рассматривать случайную величину не как дискретную, а как сплошь занимаемую какой-то интервал числовой оси.

На рисунке 6 приведена функция распределения для непрерывной случайной величины, имеющей нормальное распределение.

F(х)

х

Рисунок 6

Вероятный смысл функции распределения состоит в том, что она определяет распределение вероятности между отдельными включающими друг друга участками интервала возможных значений случайной величины.

Сформулируем общие свойства функции распределения:

1. Функция распределения F(x) есть неотрицательная функция, заключенная между 0 и 1

.

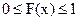2. Функция распределения F(x) есть неубывающая функция своего аргумента

при .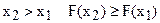

3. На минус бесконечности функция распределения равна нулю

.

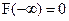4. На плюс бесконечности функция распределения равна 1

.

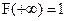Кроме того, из графика функции распределения F(x) (рисунок 6) видно, что значение функции распределения в точке разрыва определяется при подходе к этой точке слева по оси 0х. Это означает, что функция распределения непрерывна слева.

Таким образом, функция распределения F(x) любой случайной величины есть неотрицательная, неубывающая, непрерывная слева функция своего аргумента, значения которой заключены между нулем и единицей, причём 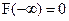; 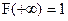. В отдельных точках эта функция может иметь скачки, на некоторых участках она может быть постоянной, на других – постоянно возрастать.

Следует также отметить, что имеет место и обратное утверждение: каждая функция, удовлетворяющая вышеперечисленным условиям, является функцией распределения некоторой случайной величины.

Функция распределения самая универсальная форма представления закона распределения случайной величины и может характеризовать как дискретные, так и непрерывные случайные величины.

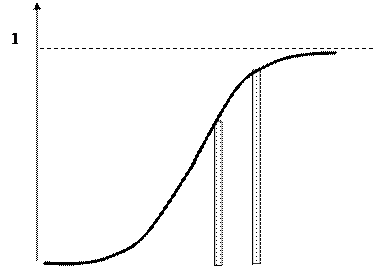
Существенным недостатком такой формы закона распределения случайной величины, как функция распределения, является то, что она не позволяет ответить на вопрос в окрестностях какой из точек а или b будет чаще появляться непрерывная величина (рисунок 7).

F(х)

F(а) F(b)

х

а b

Рисунок 7

Для более наглядного характера распределения непрерывной случайной величины в окрестностях различных точек вводится особая функция, называемая плотностью вероятности или плотностью распределения.

Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок от х до х+Dх к длине этого участка Dх, когда Dх стремится к нулю, называется плотностью распределения случайной величины в точке Х.

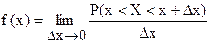
Функцию плотности распределения обозначают как f(x).

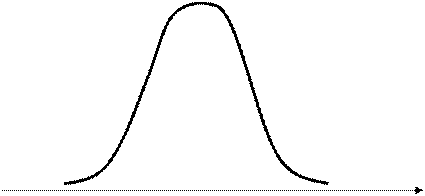
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения

На рисунке 8 приведена кривая плотности распределения непрерывной случайной величины имеющей нормальное распределение.

f(х)

0 х

Рисунок 8

Физический смысл плотности распределения заключается в том, что она указывает на то, как часто появляется случайная величина в малой окрестности точки х при повторении испытаний (рисунок 9).

F(х)

F(а) F(b)

х

а b

f(х)

f(а)

f(b)

а b х

Рисунок 9

Если в точке Х = а плотность распределения больше, чем в точке Х = b (f(а) > f(b)), то это означает, что в небольшой окрестности точки а при повторении испытаний случайная величина Х будет появляться чаще, чем в такой же по величине окрестности вокруг точки Х = b (при Dа = Db).

Плотность распределения так же, как и функция распределения, есть одна из форм закона распределения. Однако, в противоположность функции распределения, являющейся универсальной формой закона распределения, плотность распределения существует только для непрерывных случайных величин.

Сформулируем основные свойства плотности распределения:

1. Плотность распределения неотрицательна.

.

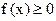2. Интеграл в бесконечных пределах от плотности распределения равен 1.

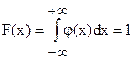
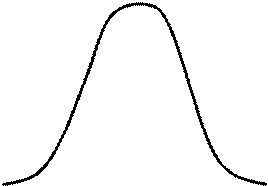
Геометрически это свойство плотности распределения означает, что вся площадь, ограниченная кривой распределения и осью абсцисс, равна 1 (рисунок 10).

f(х)

0 х

Рисунок 10

Таким образом, подводя итог вышесказанному, закон распределения дискретной случайной величины может быть задан одним из следующих способов:

· формулой, с помощью которой можно вычислить вероятность всех возможных значений случайной величины;

· рядом распределения;

· функцией распределения.

Закон распределения непрерывной случайной величины может быть задан:

· формулой, с помощью которой можно вычислить вероятность попадания случайной величины в заданный интервал;

· функцией распределения;

· функцией плотности распределения.

Дата добавления: 2014-01-03