Решение. Определение вероятности попадания случайной величины на заданный интервал с использованием таблиц приведенной функции Лапласа

Определение вероятности попадания случайной величины на заданный интервал с использованием таблиц приведенной функции Лапласа

Приведенная функция Лапласа имеет вид:

,

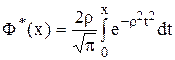где .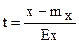

Вероятность попадания случайной величины на заданный интервал с использованием приведенной функции Лапласа определяется из выражения:

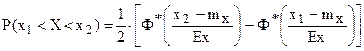
Опять видоизменим условия задачи, выбрав за начало координат центр цели, тогда: 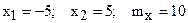(рисунок 6).

-5

ЦЦ

m_x

х₂

х₁

х

Рисунок 6

Таким образом задача сведётся к определению вероятности попадания случайной величины Х на интервал от -5 до 5, т.е. Р(-5 £ X £ 5).

Подставив значения 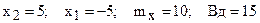в выражение для определения вероятности с помощью приведенной функции Лапласа, получим:

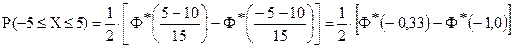
Так как функция Лапласа нечётная 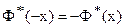, то

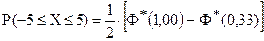
Значения приведенной функции Лапласа по известному аргументу определим из Таблицы 3 Приложения к Практикуму:

, .

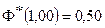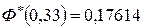Таким образом, искомая вероятность будет равна:

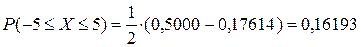
Рассчитанные значения вероятностей попадания случайной величины на заданный интервал различными способами дают достаточную близость полученных результатов.

Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 16 случаях из 100 будет получено попадание в полосу.

Сформулируем ряд основных свойств табличной функции Лапласа.

1. Функция Лапласа является неотрицательной функцией:

.

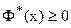2. Табличная функция Лапласа есть нечётная функция:

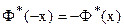
Заключительная часть занятия:

· напомнить тему и учебные вопросы занятия;

· отметить степень достижения учебных целей;

· ответить на возникшие у студентов вопросы.

На занятии иметь:

Калькуляторы – на каждого.

Задание на самостоятельную работу

Изучить:

1. Вентцель Е.С. Теория вероятностей. Учебник. Издание восьмое, стереотипное. – М.: Высшая школа, 2002 г. - 575 с., стр. 222-227

2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие. Издание десятое, стереотипное. - М.: Высшая школа», 2004 г. – 480 с. стр. 116-123.

Лекция 8 Определение дискретной случайной величины и её законы распределения

Учебные и воспитательные цели:

1. Ознакомить студентов с дискретными случайными величинами и законами их распределения.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Баврин И.И., Матросов В.Л. Высшая математика: Учебник для студентов высших учебных заведений. – М.: Гуманит. изд. центр ВЛАДОС, 2003 г. - 400 с.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия
II. Основная часть занятия
Введение в лекцию	5-10
1. Понятие случайной величины
2. Законы распределения дискретных случайных величин
Заключение по лекции
III. Заключительная часть занятия

Дата добавления: 2014-01-03