Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков

Текст лекции

Лекция 15 Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков

Учебные и воспитательные цели:

1. Дать представление об интервальных оценках параметров распределения генеральной и выборочной совокупности.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия
II. Основная часть занятия
Введение в лекцию	5-10
1. Интервальные оценки параметров распределения. Непрерывное и дискретное распределения признаков
Заключение по лекции
III. Заключительная часть занятия

Введение в лекцию:

В материалах сегодняшней лекции мы рассмотрим интервальные оценки параметров распределения, а именно непрерывное и дискретное распределения признаков генеральной и выборочной совокупности.

Учебные вопросы лекции:

Статистические ряды и их геометрическое изображение дают представление о распределении наблюдаемой случайной величины X по данным выборки. Во многих задачах вид распределения случайной величины X известен, необходимо получить приближённое значение неизвестных параметров этого распределения: т, Ϭ для нормального закона, а для закона Пуассона и другие.

Пусть 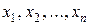- выборка наблюдений случайной величины X, а θ - неизвестный параметр.

Точечной оценкой 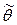неизвестного параметра θ называется приближённое значение этого параметра, полученное по выборке.

Очевидно, что 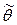зависит от элементов выборки 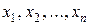. Будем считать, что 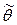- случайная величина и является функцией 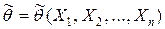системы случайных величин, одной из реализации которой является данная выборка.

Точечная оценка 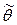должна удовлетворять свойствам:

1. Состоятельность. Оценка 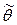параметра θ называется состоятельной, есл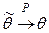и при .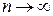

Состоятельность оценки можно установить с помощью теоремы: если

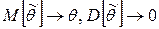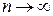при , то 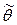- состоятельная оценка.

2. Несмещённость. Оценка 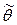параметра θ называется несмещённой,

если 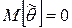. Для несмещённых оценок систематическая ошибка оценивания равна нулю.

Для оценки параметра 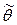может быть предложено несколько несмещённых оценок. Мерой точности 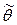считают её дисперсию 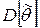. Отсюда вытекает третье свойство.

3. Эффективность. Несмещённая оценка 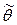параметра θ называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещёнными оценками этого параметра.

Запишем точечные оценки числовых характеристик случайной вели­чины X.

1. Точечная оценка 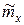математического ожидания (выборочного среднего) 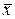находится по формуле

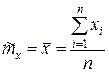. (1)

Проверим свойства оценки:

а) состоятельность следует из теоремы Чебышева: 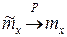при ;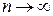

б) несмещённость:

;

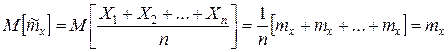в) эффективность:

,

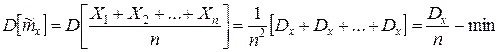так как 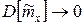при .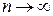

2. Точечная оценка 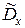дисперсии 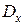находится по формуле 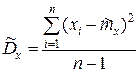, (2)

она обладает свойствами: состоятельность, несмещённость, эффективность.

3. Точечная оценка 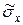среднеквадратического отклонения равна

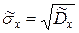. (3)

Дата добавления: 2014-01-03