Вариационные ряды

Текст лекции

Лекция 16 Характеристики вариационного ряда

Учебные и воспитательные цели:

1. Дать представление о характеристиках вариационного ряда.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия
II. Основная часть занятия
Введение в лекцию
1. Вариационные ряды
2. Построение интервального вариационного ряда
3. Графическое изображение вариационных рядов
4. Средние величины
5. Медиана и мода
6. Показатели вариации
7. Свойства эмпирической дисперсии
8. Эмпирические центральные и начальные моменты
9. Эмпирические асимметрия и эксцесс
Заключение по лекции
III. Заключительная часть занятия

Введение в лекцию:

В материалах сегодняшней лекции мы рассмотрим характеристики вариационного ряда.

Учебные вопросы лекции:

Установление закономерностей, которым подчиняются массовые случайные явления, основано на изучении статистических данных — сведений о том, какие значения принял в результате наблюдений интересующий исследователя признак.

Пример 1. Исследователь, интересующийся тарифным разрядом рабочих механического цеха, в результате опроса 100 рабочих получил следующие сведения:

5, 1, 4, 5, 4, 3, 5, 5, 2, 5, 5, 6, 4, 3, 1, 5, 2, 5, 5, 5, 3, 3, 3, 6, 6, 5, 6, 5, 3, 4, 5, 4, 6, 6, 5, 2, 1, 5, 4, 5, 5, 3, 6, 4, 5, 5, 4, 3, 5, 5, 5, 4, 5, 6; 1, 5, 2, 6, 4, 4, 3, 5, 6, 3, 5, 6, 2, 5, 4, 5, 5, 4, 6, 5, 2, 5, 3, 4, 5, 6, 5, 5, 3, 5, 4, 6, 6, 5, 5, 4, 5, 5, 6, 5, 6, 5, 5, 6, 5, 5.

Здесь признаком является тарифный разряд, а полученные о нём сведения образуют статистические данные. Для изучения данных прежде всего необходимо их сгруппировать. Расположим наблюдавшиеся значения признака в порядке возрастания. Эта операция называется ранжированием статистических данных. В результате получим следующий ряд, который называется ранжированным:

(1, 1, 1, 1) – 4 раза; (2, 2, 2, 2, 2, 2) – 6 раз; (3, 3, …, 3) – 12 раз; (4, 4, …, 4) – 16 раз; (5, 5, …, 5) – 44 раза; (6, 6, …, 6) – 18 раз.

Из ранжированного ряда следует, что признак (тарифный разряд) принял шесть различных значений: первый, второй и т.д. до шестого разряда.

В дальнейшем различные значения признака условимся называть вариантами, а под варьированием — понимать изменение значений признака. Если признак по своей сущности таков, что различные его значения не могут отличаться друг от друга меньше чем на некоторую конечную величину, то говорят, что это дискретно варьирующий признак.

Тарифный разряд — дискретно варьирующий признак: его различные значения не могут отличаться друг от друга меньше, чем на единицу. В примере этот признак принял 6 различных значений — 6 вариантов: вариант 1 повторился 4 раза, вариант 2 - 6 раз и т.д. Число, показывающее, сколько раз встречается вариант х в ряде наблюдений, называется частотой варианта т_х. Ранжированный ряд представим в виде табл. 1.

Таблица 1

Тарифный разряд х	Количество рабочих	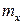Доля рабочих wx
		0,04
		0,06
		0,12
		0,16
		0,44
		0,18
Σ		1,00

Вместо частоты варианта х можно рассматривать её отношение к общему числу наблюдений п, которое называется частостью варианта х и обозначается w_x. Так как общее число наблюдений равно сумме частот всех вариантов ( 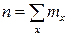), то справедлива следующая цепочка равенств: w_x=m_x/n = m_x/Σm_x.

Таблица, позволяющая судить о распределении частот (или частостей) между вариантами, называется дискретным вариационным рядом.

В примере 1 была поставлена задача изучить результаты наблюдений. Если просмотр первичных данных не позволил составить представление о варьировании значений признака, то, рассматривая вариационный, ряд, можно сделать следующие выводы: тарифный разряд колеблется от 1-го до 6-го; наиболее часто встречается 5-й тарифный разряд; с ростом тарифного разряда (до 5-го разряда) растёт число рабочих, имеющих соответствующий разряд.

Наряду с понятием частоты используют понятие накопленной частоты, которую обозначают 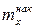. Накопленная частота показывает, во скольких наблюдениях признак принял значения, меньшие заданного значения х. Отношение накопленной частоты к общему числу наблюдений называют накопленной частостью и обозначают 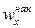. Очевидно, что .

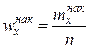В дискретном вариационном ряду накопленные частоты (частости) вычисляются для каждого варианта и являются результатом последовательного суммирования частот (частостей). Накопленные частоты (частости) для вариационного ряда, заданного в табл. 1, вычислены в табл. 2.

Таблица 2

Тарифный разряд х	Количество рабочих	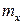Накопленная частота	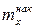Накопленная частость
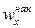
			0,00
		0 + 4=4	0,04
		4 + 6=10	0,10
		10+12=22	0,22
		22 + 16=38	0,38
		38 + 44=82	0,82
Выше 6		82+ 18=100	1,00

Например, варианту 1 соответствует накопленная частота, равная нулю, так как среди опрошенных рабочих не было таких, у которых тарифный разряд был бы меньше 1-го; варианту 5 соответствует накопленная частота 38, так как было 4+6+12+16 рабочих с тарифным разрядом, меньшим 5-го, накопленная частость для этого варианта равна 0,38 (38: 100); если тарифный разряд выше 6-го, то ему соответствует накопленная частота 100, так как тарифный разряд всех опрошенных рабочих не выше 6-го.

Пример 2. Исследователь, изучающий выработку на одного рабочего-станочника механического цеха в отчётном году в процентах к предыдущему году, получил следующие данные (в целых процентах) по 117 рабочим:

111, 85, 85, 91, 101, 109, 86, 102, 111, 98, 105, 85, 112, 113, 87, 109, 109, 115, 99, 105, 111, 94, 107, 99, 107, 125, 89, 104, 113, 96, 103, 145, 104, 105, 88, 103, 97, 115, 109, 89, 108, 107, 97; 106, 107, 96, 109, 116, 109, 117, 108, 109, 139, 116, 117, 103, 127, 119, 118, 125, 105, 116, 117, 106, 101, 113, 107, 105, 119, 107,119, 111, 112, 129, 113, 106, 104, 106, 98, 123, 108, 93, 105, 106, 139, 108, 109, 93, 107, 117, 107, 118, 99, 108, 108, 119, 98, 108, 101, 109, 109, 128, 128, 127, 121, 118, 122, 116, 124, 125, 114, 126, 131, 141, 143.

В этом примере признаком является выработка в отчётном году в процентах к предыдущему. Очевидно, что значения, принимаемые этим признаком, могут отличаться одно от другого на сколь угодно малую величину, т. е. признак может принять любое значение в некотором числовом интервале (только для упрощения дальнейших расчетов полученные данные округлены до целых процентов). Такой признак называют непрерывно варьирующим. По приведенным данным трудно выявить характерные черты варьирования значений признака. Построение дискретного вариационного ряда также не даст желаемых результатов (слишком велико число различных наблюдавшихся значений признака). Для получения ясной картины объединим в группы рабочих, у которых величина выработки колеблется, например, в пределах 10%. Сгруппированные данные представим в табл. 3.

Таблица 3

Выработка в отчётном году в % к предыдущему (интервалы)	Количество рабочих	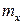Доля рабочих w	Накопленная частота	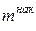Накопленная частость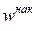
80-90		8/117		8/117
90-100		15/117		23/117
100-110		46/117		69/117
110-120		29/117		98/117
120-130		13/117		111/117
130-140		3/117		114/117
140-150		3/117		117/117
Σ

В табл. 3 частоты m показывают, во скольких наблюдениях признак принял значения, принадлежащие тому или иному интервалу. Такую частоту называют интервальной, а отношение её к общему числу наблюдений — интервальной частостью w. Таблицу, позволяющую судить о распределении частот (или частостей) между интервалами варьирования значений признака, называют интервальным вариационным рядом.

Интервальный вариационный ряд, представленный в табл. 3, позволяет выявить закономерности распределения рабочих по интервалам выработки. В табл. 3 для верхних границ интервалов приведены накопленные частоты (частости) (они получены последовательным суммированием интервальных частот (частостей), начиная с частоты (частости) первого интервала). Например, для верхней границы третьего интервала, равной 110, накопленная частота равна 69; так как 8+15+46 рабочих имели выработку меньше 110%, накопленная частость равна 69/117.

Интервальный вариационный ряд строят по данным наблюдений за непрерывно варьирующим признаком, а также за дискретно варьирующим, если велико число наблюдавшихся вариантов. Дискретный вариационный ряд строят только для дискретно варьирующего признака.

Иногда интервальный вариационный ряд условно заменяют дискретным. Тогда серединное значение интервала принимают за вариант х, а соответствующую интервальную частоту — за .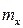

Дата добавления: 2014-01-03