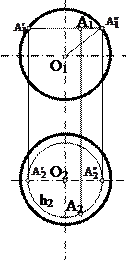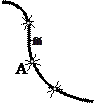Лекция №9
Лекция
Айналу беттері. Айналу беттеріндегі нүкте мен түзулер
Айналу беттері ℓ (жасаушы) сызығын айналу осі - i түзуінің бойымен айналдырғанда алынады. Барлық айналу беттерінің жалпы жағдайда, бірдей анықтаушысы болады:
|
|
| анықтаушының геометриялық бөлігі екі элементтен - ℓ жасаушысынан және i айналу осінен тұрады; алгоритмдік бөлігі i осінің бойымен ℓ жасаушысының айналу шартын құрайды ГА{ℓ, i } АА |ℓ i |.
ℓ жасаушының нүктелері i, осінің бойымен шеңбер жасап айналады, сондықтан айналу беттерінің барлығы циклдік беттер болады.
| |
1-cурет
|
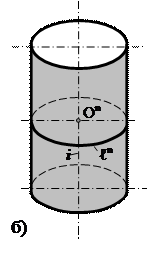
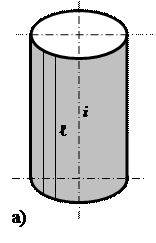
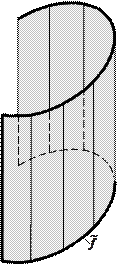
Мысалы, айналу цилиндр беті сызықты қаңқа (оске параллель түзусызықты жасаушылар жиыны), циклдік (оске перпендикуляр шеңберлер жазықтықтарының жиынтығы) (1а, б-суреттер) болуы мүмкін.
Айналу бетінде жатқан шеңберлер бірі-біріне параллель жазықтықтарда жатқандықтан, оларды параллелдер, ал беттердің жазықтықтармен қиылысу осі арқылы өтетін жазық сызықтарын меридиандар деп атайды .
Түзусызықты айналу беттері
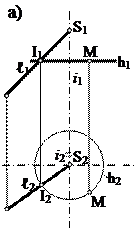
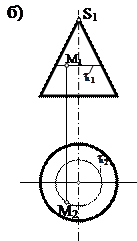
Айналу конусы ℓ түзуін өзімен қиылысатын i осінің төңірегінде айналдырғанда пайда болады. Беттің анықтаушысы мына түрде жазылады: ГА {ℓ, i }, АА |ℓ È i, ℓ ∩ i |. Сызбада конусты геометриялық анықтаушының элементтерінің проекцияларымен (3а-сурет) немесе p1 және p2 жазықтықтарындағы очерктерімен беруге болады (3б-сурет). Конус бетіндегі нүкте h параллелдері арқылы анықталады.
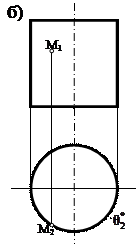
Айналу цилиндрі ℓ түзуін өзіне параллель остің төңірегінде айналдырғанда пайда болады. Цилиндрдің анықтаушысы мына түрде жазылады: ГА {ℓ, i }, АА |ℓ i, ℓ || i |. 4-суретте цилиндр анықтаушысының элементтерінің проекциясымен және очеркімен берілген:
Айналу цилиндр беті – проекциялаушы. Оның проекциясы p2 жазық-тығында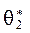 шеңберге айналады. Сондықтан М нүктесін оның бетінде салу жеңілдейді, өйткені М2 Î шеңберге айналады. Сондықтан М нүктесін оның бетінде салу жеңілдейді, өйткені М2 Î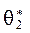 . .
|
|
| Бірқуысты айналу гипер-болоиды жасаушысының өзімен айқас оспен айналғанда пайда болады. 5-суретте айналу гиперболоиды:
– өзінің анықтаушысының про-екциясымен: ГА{ℓ, i },
АА |ℓ i, ℓ ×/ i | (5 а-сурет);
-- очерктерімен, p1 жазықтығында– d1 гиперболосымен, p2 жазықтығында с2 мойнымен (5б-сурет) берілген.
| |
| |
5-сурет
|
|
Түзу сызықтық емес айналу беттері.
Сфера (ℓ) шеңберін өзінің (i) диаметрі төңірегінде айналдырғанда пайда болады. Сфераның анықтаушысы мына түрде жазылады: ГА{ℓ, i }, АА |ℓ i, бұл жерде ℓ – шеңбер. Сызбада сфера мына түрде берілуі мүмкін:
- анықтаушысының элементтерінің проекцияларымен (6 а-сурет);
- очерктерімен: p1 және p2 жазықтықтарында диаметрлері бірдей (6б-сурет) шеңберлермен:
 = O2 = O2
|
|
        а) а)
| б)
| а)
| б)
| |
6-сурет
|
7-сурет
|
Сфера бетіндегі экватор q және бас меридиан ℓ ерекше сызықтар болып саналады. М нүктесін сфера бетінде салу үшін h параллелдерін қолданады.
Тор ℓ шеңберінің өзінің i хордасының (жабық тор) (7а-сурет) немесе шеңбер жазықтығында жататын, бірақ одан сырт орналасқан i, түзуінің төңірегінде айналдырғанда пайда болады (7б-сурет). Екінші жағдайда тор ашық тор деп аталады
Айналу беттері басқа да екінші реттік қисықтардың айналуынан пайда болуы мүмкін:
– эллипсті остерінің бірінің төңірегінде айналдырғанда айналу эллипсоидасы пайда болады (8а-сурет);
– гиперболаны жорамал осінің төңірегінде айналдырғанда бірқуысты айналу гиперболоиды (8б-сурет), ал гиперболаны нақты осінің төңірегінде айналдырғанда екіқуысты айналу гиперболоиды (8в-сурет) пайда болады;
– параболаны өзінің осінің төңірегінде айналдырғанда айналу параболоиды (8г-сурет) құрылады.
Есеп. Өзінің анықтаушыларының проекцияларымен берілген сфераның очеркін салу керек: ГА q {O, A}, бұл жерде О – сфераның центрі, А Î q (9-сурет).
p1 және p2 жазықтықтарындағы сфераның очерктері диаметрі бірдей шеңберлер болады. Есептің шешуі осы шеңберлердің радиустарын табуға келтіріледі.
Берілген А нүктесі сызатын h параллелді пайдаланып (9-сурет), А нүктесінің шеткі (сол немесе оң) қалпын А¢ немесе А¢¢ нүктелерін анықтаймыз. О1А1¢¢ кесіндісі шеңбердің радиусын анықтайды, яғни R=÷ О1А1¢¢ê.
Есеп. m сызығы конус бетінде орналасқан. Осы сызықтың түрін (түзу немесе қисық) анықтау және оның горизонталь проекциясын салу керек (10-сурет).
 Конус бетіндегі түзулердің үйірі жасаушылар екені белгілі. m сызығы жасаушы бола алмайды, өйткені m1 ' S1. Сондықтан, m сызығы – қисық, дәлірек айтқанда, эллипс және оның горизонталь проекциясы да қисық (эллипс) болады. m2 сызығын графикалық түрде салу үшін оның дискретті нүктелер жиынын: {М, М¢, М¢¢, … Мn} салу жеткілікті. Ол үшін конус бетінің (h) параллелдерін пайдаланамыз. Конус бетіндегі түзулердің үйірі жасаушылар екені белгілі. m сызығы жасаушы бола алмайды, өйткені m1 ' S1. Сондықтан, m сызығы – қисық, дәлірек айтқанда, эллипс және оның горизонталь проекциясы да қисық (эллипс) болады. m2 сызығын графикалық түрде салу үшін оның дискретті нүктелер жиынын: {М, М¢, М¢¢, … Мn} салу жеткілікті. Ол үшін конус бетінің (h) параллелдерін пайдаланамыз.
Жазылмайтын түзусызықты қиғаш беттер.
Түзусызықты беттер кеңістікті толтыратын төрт параметрлі сызықтар жиынының үш параметрін байланыстырғанда пайда болады.
Кеңістікте кез-келген 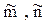 және және 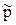 кеңіс қисықтары берілген болсын. Енді берілген түзулерді қандай түзулер жиыны қиятынын көрсетейік: кеңіс қисықтары берілген болсын. Енді берілген түзулерді қандай түзулер жиыны қиятынын көрсетейік:
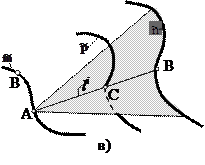
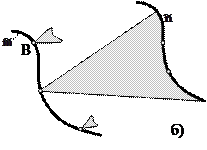
а) 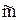 қисығын екі параметрлі жиын – түзулер тобы немесе үш параметрлі жиын – түзулер комплексі қиюуы мүмкін (11а-сурет); қисығын екі параметрлі жиын – түзулер тобы немесе үш параметрлі жиын – түзулер комплексі қиюуы мүмкін (11а-сурет);
б) 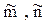 қисықтары конустық беттердің бір параметрлі жиынын немесе екі параметрлі – түзулердің конгруэнттілігін қиып өтуі мүмкін (11б-сурет); қисықтары конустық беттердің бір параметрлі жиынын немесе екі параметрлі – түзулердің конгруэнттілігін қиып өтуі мүмкін (11б-сурет);
в) 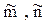 және және 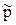 қисықтары кейбір сызықтық беттердің ℓ i жасаушыларының бір параметрлі жиынын қиып өтуі мүмкін (11в-сурет). қисықтары кейбір сызықтық беттердің ℓ i жасаушыларының бір параметрлі жиынын қиып өтуі мүмкін (11в-сурет).
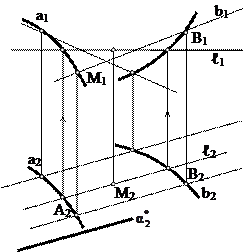
Дискретті түзусызықты бет қаңқасын салу үшін сызықтарының бірінен (мысалы, 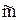 сызығынан) берілген бір интервалда алынған А, В, …нүктелерін белгілеп және олар арқылы беттің ℓ i жасаушыларын жүргізу керек. Бұл жерде жасаушылар айқас түзулер болады. сызығынан) берілген бір интервалда алынған А, В, …нүктелерін белгілеп және олар арқылы беттің ℓ i жасаушыларын жүргізу керек. Бұл жерде жасаушылар айқас түзулер болады.
Сонымен, жалпы түрдегі түзусызықтық беттерді берілген бір қоз-ғалмайтын бағыттаушы бойымен ℓ жасаушыларының қозғалысы нәтижесінде алынады деп қарастыруға болады. Түзусызықты беттердің жасаушыларының қозғалысы жалпы жағдайда үш бағыттаушымен толық анықталады. Беттің геометриялық анықтаушысы бұл жағдайда мына түрде беріледі: q {m, n, р}, бұл жерде m, n және р сызықтары – бағыттаушылар. Бағыттаушылардың түрлері мен қалыптарына байланысты түзусызықты беттердің әртүрлі жиындарын алуға болады. Бағыттаушылар түзу немесе қисық, өзіндік немесе өзіндік емес болулары мүмкін.
Қаңқаның түзу сызықтары берілген m, n және р айқас түзулерін қиып өтетін болса, онда бетті бірқуысты гиперболоид (12-сурет) деп атайды. Бет қаңқасын салуды жеңілдету үшін түзулердің біреуін (мысалы, р түзуін) проекциялаушы қалыпта береміз.
q бетінің анықтаушысы мына түрде жазылады: ГА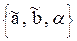 ,бұл жерде a –параллелизм жазықтығы. АА q |ℓ i ∩ ,бұл жерде a –параллелизм жазықтығы. АА q |ℓ i ∩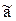 ,ℓ i ∩ ,ℓ i ∩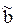 , ℓ i || a|. Цилиндроид бетінде М нүктесін салу үшін ℓ жасаушысын жүргізеді және одан ізделінген М нүктесін белгілейді. , ℓ i || a|. Цилиндроид бетінде М нүктесін салу үшін ℓ жасаушысын жүргізеді және одан ізделінген М нүктесін белгілейді.
Коноид түзусызықты ℓ жасаушысының а және b (а-түзу, b-қисық) екі бағыттаушының бойымен қозғалғанда пайда болады (15-сурет).
Беттің анықтаушысы былай жазылады: ГА q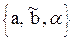 , бұл жерде a – параллелизм жазықтығы. АА q |ℓ i ∩ , бұл жерде a – параллелизм жазықтығы. АА q |ℓ i ∩ 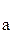 ,ℓ i ∩ ,ℓ i ∩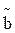 , ℓ i || a. 15-суретте кез-келген М нүктесін коноид бетінде салу көрсетілген (ℓ Ì q, М Î ℓ): , ℓ i || a. 15-суретте кез-келген М нүктесін коноид бетінде салу көрсетілген (ℓ Ì q, М Î ℓ):
Түзусызықты жазылатын беттер.
Қаңқаның шексіз жақын сызықтарының әрбір жұбы айқас болатын қиғаш түзусызықты беттерден жазылатын түзусызықты беттерден айыр-машылығы қиылысатындығында. Жазылатын түзусызықты беттерді қабыр-ғаларының ені нольге жақын қабырғалары беттердің шекаралық қалпы ретінде көрсетуге болады. Сондықтан мұндай бетті көпжақты бет сияқты жазықтыққа жазуға болады.
Конустық бетте бұл нүкте оның төбесі (17-сурет), ал цилиндрлік бетте түзу сызықты жасаушылардың шексіз алыста орналасқан қиылысу нүктесі (18-сурет).
Тұйық беттер - геометриялық денелер: призма, пирамида, конус, цилиндр және басқалар тәжірибеде көп қолданылады.
Геометриялық денелерге жақсы көрнекілік беру үшін оларды p1 және p2 жазықтықтарында очерктерімен кескіндейді.
19-суретте кескінделген:
а) үшжақты көлбеу пирамида;
б) үшжақты көлбеу призма;
в) бағыттаушысы f кез-келген тұйық қисық болуы мүмкін жалпы түрдегі конус.
Позициялық есептер. Жазықтықпен жазықтықтың қиылысуы.
Позициялық есептерге геометриялық денелердің бірін-бірімен салыстыр-ғандағы өзара орналасуын анықтайтын есептер жатады. Мысалы, геометриялық элементтердің қиылысуы және өзара қатыстылығына арналған есептер. Біз осы уақытқа дейін кейбір позициялық есептерді келтіргенбіз, мысалы, нүктені жазықтыққа, бетке салу, сызықты жазықтыққа, бетке салу.
Позициялық есептерді шешкенде бәсекелес элементтер қолданылады. Енді соларды кеңірек қарастырайық.
Анықтама: Бір кескіндеуші жазықтықта орналасқан екі түзуді немесе қисық сызықтарды бәсекелес деп атайды.
  Өзара қиылысатын а және b (сурет 1) түзулері горизанталь бәсекелес түзу-лер болады, а ¯ b: а ¯ b Þ а 2 = b 2 . Өзара қиылысатын а және b (сурет 1) түзулері горизанталь бәсекелес түзу-лер болады, а ¯ b: а ¯ b Þ а 2 = b 2 .
m және n параллель түзулері фронталь бәсекелес
  m n: m n Þ m1 = n1 (сурет 2). m n: m n Þ m1 = n1 (сурет 2).
c түзуі мен d қисығы – горизонталь бәсекелес
  с ¯ d: c ¯ d Þ d 2 Ì с 2 (сурет 3) с ¯ d: c ¯ d Þ d 2 Ì с 2 (сурет 3)
              а1
b1
a2=b2 а1
b1
a2=b2
| m1= n1
n2
m2
| c 1
d 1
d 2 = c 2
| | Сурет 1
| Сурет 2
| Сурет 3
|
|

 Айналу осі
Айналу осі














 шеңберге айналады. Сондықтан М нүктесін оның бетінде салу жеңілдейді, өйткені М2 Î
шеңберге айналады. Сондықтан М нүктесін оның бетінде салу жеңілдейді, өйткені М2 Î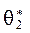 .
.
















































 а)
а)






























 Конус бетіндегі түзулердің үйірі жасаушылар екені белгілі. m сызығы жасаушы бола алмайды, өйткені m1 ' S1. Сондықтан, m сызығы – қисық, дәлірек айтқанда, эллипс және оның горизонталь проекциясы да қисық (эллипс) болады. m2 сызығын графикалық түрде салу үшін оның дискретті нүктелер жиынын: {М, М¢, М¢¢, … Мn} салу жеткілікті. Ол үшін конус бетінің (h) параллелдерін пайдаланамыз.
Конус бетіндегі түзулердің үйірі жасаушылар екені белгілі. m сызығы жасаушы бола алмайды, өйткені m1 ' S1. Сондықтан, m сызығы – қисық, дәлірек айтқанда, эллипс және оның горизонталь проекциясы да қисық (эллипс) болады. m2 сызығын графикалық түрде салу үшін оның дискретті нүктелер жиынын: {М, М¢, М¢¢, … Мn} салу жеткілікті. Ол үшін конус бетінің (h) параллелдерін пайдаланамыз.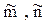 және
және 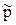 кеңіс қисықтары берілген болсын. Енді берілген түзулерді қандай түзулер жиыны қиятынын көрсетейік:
кеңіс қисықтары берілген болсын. Енді берілген түзулерді қандай түзулер жиыны қиятынын көрсетейік: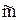 қисығын екі параметрлі жиын – түзулер тобы немесе үш параметрлі жиын – түзулер комплексі қиюуы мүмкін (11а-сурет);
қисығын екі параметрлі жиын – түзулер тобы немесе үш параметрлі жиын – түзулер комплексі қиюуы мүмкін (11а-сурет);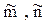 қисықтары конустық беттердің бір параметрлі жиынын немесе екі параметрлі – түзулердің конгруэнттілігін қиып өтуі мүмкін (11б-сурет);
қисықтары конустық беттердің бір параметрлі жиынын немесе екі параметрлі – түзулердің конгруэнттілігін қиып өтуі мүмкін (11б-сурет);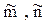 және
және 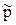 қисықтары кейбір сызықтық беттердің ℓ i жасаушыларының бір параметрлі жиынын қиып өтуі мүмкін (11в-сурет).
қисықтары кейбір сызықтық беттердің ℓ i жасаушыларының бір параметрлі жиынын қиып өтуі мүмкін (11в-сурет).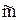 сызығынан) берілген бір интервалда алынған А, В, …нүктелерін белгілеп және олар арқылы беттің ℓ i жасаушыларын жүргізу керек. Бұл жерде жасаушылар айқас түзулер болады.
сызығынан) берілген бір интервалда алынған А, В, …нүктелерін белгілеп және олар арқылы беттің ℓ i жасаушыларын жүргізу керек. Бұл жерде жасаушылар айқас түзулер болады.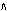
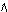




























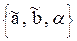 ,бұл жерде a –параллелизм жазықтығы. АА q |ℓ i ∩
,бұл жерде a –параллелизм жазықтығы. АА q |ℓ i ∩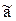 ,ℓ i ∩
,ℓ i ∩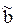 , ℓ i || a|. Цилиндроид бетінде М нүктесін салу үшін ℓ жасаушысын жүргізеді және одан ізделінген М нүктесін белгілейді.
, ℓ i || a|. Цилиндроид бетінде М нүктесін салу үшін ℓ жасаушысын жүргізеді және одан ізделінген М нүктесін белгілейді.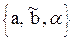 , бұл жерде a – параллелизм жазықтығы. АА q |ℓ i ∩
, бұл жерде a – параллелизм жазықтығы. АА q |ℓ i ∩ 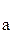 ,ℓ i ∩
,ℓ i ∩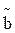 , ℓ i || a. 15-суретте кез-келген М нүктесін коноид бетінде салу көрсетілген (ℓ Ì q, М Î ℓ):
, ℓ i || a. 15-суретте кез-келген М нүктесін коноид бетінде салу көрсетілген (ℓ Ì q, М Î ℓ):














































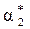 );
2. М Î ℓ.
);
2. М Î ℓ.



































 а)
а)

 Өзара қиылысатын а және b (сурет 1) түзулері горизанталь бәсекелес түзу-лер болады, а ¯ b: а ¯ b Þ а 2 = b 2 .
Өзара қиылысатын а және b (сурет 1) түзулері горизанталь бәсекелес түзу-лер болады, а ¯ b: а ¯ b Þ а 2 = b 2 .
 m n: m n Þ m1 = n1 (сурет 2).
m n: m n Þ m1 = n1 (сурет 2).
 с ¯ d: c ¯ d Þ d 2 Ì с 2 (сурет 3)
с ¯ d: c ¯ d Þ d 2 Ì с 2 (сурет 3)












 а1
b1
a2=b2
а1
b1
a2=b2