Статистические характеристики

Вариационный ряд чисел и его основные

В результате выборки мы получим ряд значений варьирующего признака. Этот ряд называется вариационным рядом чисел. Каждое в отдельности наблюдение является представителем или элементом вариационного ряда.

Чтобы выявить определённую закономерность при анализе вариационного ряда чисел часто подходят двумя путями:

1. Можно группировать эти данные (не сводить их в таблицу, не разбивать их на группы), но это неудобно!

2. Данные группируют. Разбивают на классы или группы.

Последовательность группировки этих данных заключается:

а) устанавливают количество групп или классов. Оно зависит от объёма выборки (n)

n k

20 - 30 5 - 6

30 – 60 6 – 7

60 – 100 7 – 8

> 100 8 - 15

_{__}

б) К = 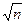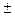2 Количество классов берётся от 5 до 20

в) Устанавливают интервал или классовый промежуток

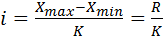, где

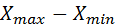– размах варьирования (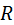), разница между наибольшим (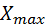) и наименьшим (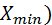значениями признака.

г) Затем данные разносят по классам и рассчитывают характеристики вариационного ряда.

1. Средняя арифметическая выборки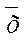

2. Дисперсия (средний квадрат отклонений) S²

3. Стандартное отклонение или среднее квадратическое S

4. Коэффициент вариации V

5. Ошибка средней арифметической (в абсолютных единицах)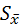

6. Относительная ошибка средней арифметической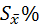

7. Доверительный интервал 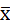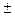t

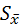
Составляется вспомогательная таблица, в которой вычисляются средняя арифметическая (), отклонения от средней (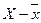), квадраты отклонений 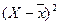и суммы квадратов отклонений .

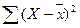1. Х_прост. и Х_взвеш – это обобщенная характеристика вариационного ряда (изменчивость)

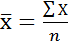
- средняя арифметическая 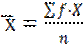- средняя арифметическая

простая, применяется при n – не более 10. взвешенная, применяется при n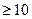

Правильность вычисления 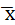проверяется по равенству 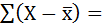0 в несгруппированном ряду и 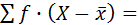0 в сгруппированном (если 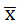найдена без остатка).

Средняя арифметическая – обобщённая характеристика всей совокупности в целом, но она не показывает степень изменчивости признака. Часто у двух вариационных рядов 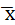бывает одинакова, а отклонения индивидуальных значений признака от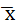различны, поэтому для характеристики степени изменчивости вариационного ряда находят показатели вариации (изменчивости) – дисперсию, стандартное отклонение и коэффициент вариации.

2. Затем рассчитывается дисперсия (S² ), показатель, характеризующий среднюю меру изменчивости.

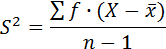
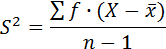
где n –1 – число степеней свободы (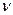_мю) где f – частота класса

3. Стандартное отклонение ( 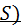. Размерность дисперсии и средней арифметической не совпадает: единица измерения первой – в квадрате, а второй – без квадрата. Поэтому, извлекая квадратный корень из 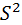, находят показатель варьирования – среднее квадратическое, или стандартное отклонение 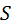– это средняя ошибка отдельного наблюдения, взятого из данной совокупности. Измеряется она в тех же единицах, что и изучаемый признак, и вычисляется по формулам

в несгруппированном вариационном ряду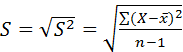

в сгруппированном вариационном ряду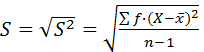

4. Коэффициент вариации (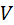) - стандартное отклонение, выраженное в процентах к средней арифметической.

(%)/

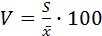Коэффициент вариации является показателем однородности или выравненности объектов по изучаемому признаку. Изменчивость вариационного ряда считается:

незначительной – при 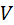до 10%;

средней – при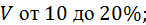

значительной – при 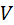больше 20%.

В селекции и семеноводстве используют коэффициент выравненности (величина дополняющая коэффициент вариации до 100 %).

В + V = 100 % В = 100 – V

5. Ошибка средней арифметической (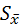). Средняя арифметическая выборочной совокупности (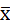) отличается от средней арифметической всей генеральной совокупности на величину ошибки 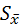, с которой определена средняя выборочной совокупности (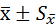). 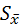прямо пропорциональна стандартному отклонению (S) и обратно пропорциональна корню квадратному из числа наблюдений (n):

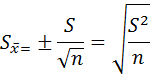
Если вместо S подставить его значение (для несгруппированного вариационного ряда), то формула примет вид:

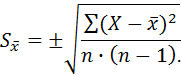
Абсолютная ошибка (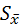) позволяет:

а) установить величину случайной ошибки в опыте;

б) оценить существенность различий между средними урожаями по вариантам;

в) рассчитать доверительный интервал

6. Относительная ошибка средней арифметической (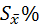). Сопоставляя среднюю арифметическую 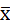с её ошибкой 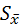, можно получить представление о точности определения :

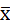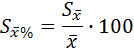
Чем меньше числовое значение 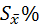, тем точнее проведено наблюдение, т.е. с меньшей ошибкой определена 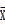. Таким образом, по значению относительной ошибки можно оценить точность определения средней арифметической.

При значении показателя 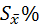1-2% - точность определения выборочной средней отличная, 2-3% - хорошая, 3-5% - вполне удовлетворительная, 5-7% - удовлетворительная, больше 7% - неудовлетворительная

Раньше 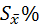- использовали для оценки качества выполнения полевого опыта и считали, что если 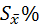, больше 7-8 % то опыт нужно браковать. Но это не объективно т.к. относительная ошибка зависит от 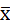и чем больше 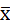, тем меньше 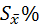при одном и том же числе наблюдений.

7. Доверительный интервал (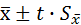). Величина 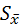даёт возможность вычислить пределы, в которых находится средняя генеральной совокупности, - доверительный интервал для средней. Границы доверительного интервала равны 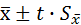. Значение 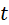дано в приложении 2 для принятого уровня значимости (05 или 01) и числа степеней свободы n – 1.

Дата добавления: 2014-01-03