Нахождение параметров выборочных уравнений прямой линии регрессии

Пусть в результате 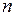независимых опытов получены 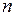пар значений системы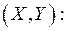 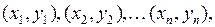которые могут быть заданы (табл. 1). По этим статистическим данным найдем сначала параметры (коэффициенты) уравнения (3) регрессии 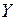на

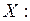
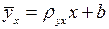(5)

Так как различные значения 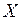и соответствующие им значения 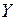наблюдались по одному разу, то группировать данные нет необходимости; также нет надобности использовать понятие условной средней (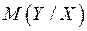−условное матожидание 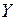при конкретном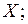 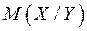− условное матожидание 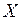при конкретном 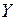), поэтому уравнение (3) можно записать:

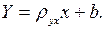(6)

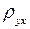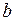Подберем параметры и так, чтобы точки 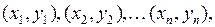построенные по данным наблюдениям на плоскости 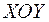лежали как можно ближе к прямой (5).

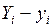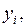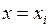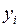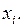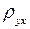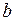Разность – является отклонением ординаты вычисленной с помощью уравнения (5) при от наблюдаемой ординаты (табличное значение), соответствующей значению Используем в дальнейшем метод наименьших квадратов, а именно подберем и так, чтобы сумма квадратов отклонений была минимальной, т.е. составим функцию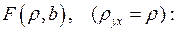

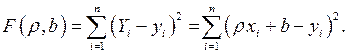
Исследуем функцию 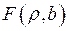на минимум, приравниваем к нулю ее частные производные 1-го порядка:

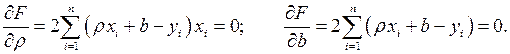(7)

Получим систему двух линейных уравнений относительно 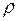и

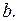
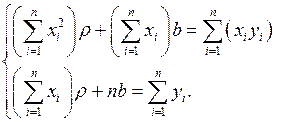(8)

Решив эту систему, получим: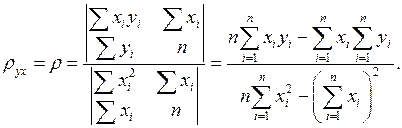

Применяя безындексную форму:

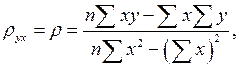
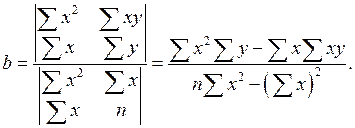
Аналогично можно найти выборочные уравнения прямой линии регрессии 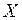на 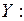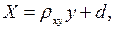формулы для параметров 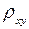и 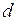имеют вид:

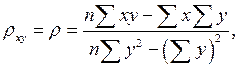
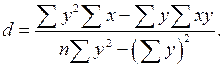
Однако иногда уравнение регрессии (5) удобно записать в другой форме, вводя выборочный коэффициент корреляции. Найдя 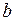из уравнения второго системы (8) и подставляя в уравнение (5), получим:

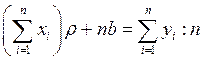
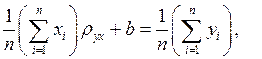
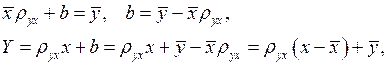
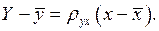(9)

Если ввести соотношени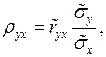е где

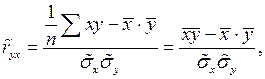(10)

(10) – выборочный коэффициент корреляции.

Действительно,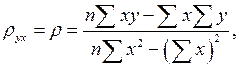

разделим числитель и знаменатель на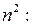

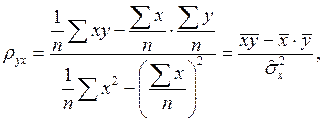но 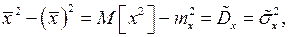отсюда

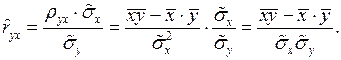Тогда

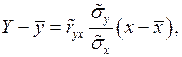(11)

(11) – выборочное уравнение регрессии 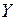на 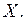Аналогично находится выборочное уравнение линейной регрессии 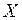на .

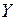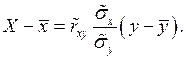(12)

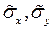−выборочные средние квадратические отклонения

Пример 1. Методами корреляционного анализа исследовать зависимость между урожайностью пшеницы и картофеля на соседних участках на основании статистических данных (США). Построить выборочное уравнение линейной регрессии.

Таблица 2

Годы:
Урожай пшеница (ц)	20,1	23,6	26,3	19,9	16,7	23,2	31,9	33,5
Урожай картофель(т)	7,2	7,1	7,4	6,1	6,0	7,3	9,4	9,2

Дата добавления: 2014-01-03