Основное уравнение гидростатики

Рассмотрим объем жидкости, находящейся в покое под дейст­вием сил тяжести и давления на свободной поверхности. Опре­делим гидростатическое давление Р в т. А на бесконечно малой площадке dS, расположенной на глубине h от свободной поверхности жидкости и параллельной ей (рис.). Выделим над этой площадкой некоторый цилиндрический объем жидкос­ти, заменив действие окружающей его среды силами давления на свободную поверхность РodS, на нижнее основание цилиндра РdS и на его боковую поверхность. Силы давления жидкости на боковую поверхность цилиндра взаимно уравновешиваются. На выделенный объем действует также массовая сила — вес G = g h dS. Цилиндр находится в равновесии, поэтому сумма проекций всех сил на ось z будет равна нулю:

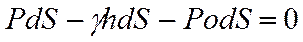
Сократив члены этого уравнения на dS и перегруппировав их, получим основное уравнение гидростатики:

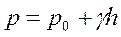
где P—полное или абсолютное давление, иногда обозначаемое как Pабс,gh — весовое давление, равное весу столба жидкости при единичной площа­ди и высоте h; z и z₀ — геометрические высоты расположения точек относительно произвольной горизонтальной плоскости называемой плоскостью сравнения

Если в уравнении заменить h на z-z₀, то получим

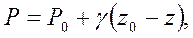
откуда пр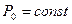и и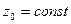

(для точек лежащих на свободной поверхности) имеем

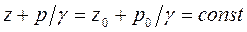
т. е. другую форму записи основного уравнения гидростатики,

где P/ g и P₀/ g —высоты, соответствующие гидростатиче­скому давлению P и P о. Величины z и P / g часто в гидрав­лике называют геометрической и пьезометрической высотами или геометри­ческим и пьезометрическим напорами.

Поскольку все слагаемые, входящие в уравнение

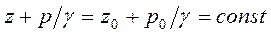
име­ют линейную размерность, то и сумма высот z+P/g будет также высотой Н с линейной размерностью. Высоту Н называют гидро­статическим напором. А горизонтальную плоскость, удаленную от плоскости сравнения на величину гидростатического напора Н называют плоскостью гидростати­ческого напора. Эта плоскость расположена выше плоскости свободной поверхности на высо­ту P₀/ g. Итак, для данного объе­ма жидкости гидростатический напор относительно выбранной плоскости сравнения - величина постоянная:

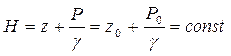
С энергетической точки зрения рассматриваемое уравнение представля­ет собой постоянную величину суммы удельной потенциальной энергии положения z и удельной потенциальной энергии давле­ния P/ g во всех точках покоящейся жидкости относительно плос­кости сравнения.

Из основного уравнения гидростатики следует, что гидростатическое давление Р в любой точке жидкости и на любой глубине h зависит от внешнего давления Ро на свободной поверхности, т. е. всякое внешнее давление, действующее на свободную поверхность жид­кости, находящейся в равновесии, передается внутрь во все точ­ки жидкости без изменения. В этом заключается закон Паскаля, найденный опытным путем и имеющий большое практическое значение.

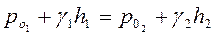
Рассмотрим равновесие двух неоднородных жидкостей (g_{1 ¹} g₂), покоящихся в сообщающихся сосудах (рис.):

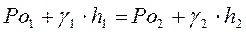
если Ро₁ = Ро₂ = Ро, то h₁/h₂=g₂/g₁; h₁/h₂=r₂/r₁ т.е. неод­нородных жидкостях и одинаковом внешнем давлении в сообща­ющихся сосудах уровень жидкостей обратно пропорционален удельному весу этих жидкостей.

Для однородных жидкостей (g₂=g₁) свободная поверхность в сообщающихся сосудах устанавливается на одном уровне (h₁=h₂).

Дата добавления: 2014-01-03