
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для закрытого сосуда
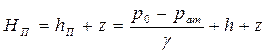
В точке размещения пьезометра избыточное гидростатическое давление
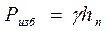 , откуда
, откуда
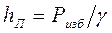
Абсолютное гидростатическое давление 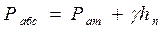 Внешнее давление, действующее на поверхность жидкости в закрытом резервуаре,
Внешнее давление, действующее на поверхность жидкости в закрытом резервуаре, 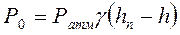 , откуда
, откуда
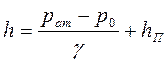
Пьезометры применяют для измерения небольшого давления десятых и сотых долей атмосферного давления. Пьезометрическую высоту измеряют в метрах столба жидкости. Длина трубки пьезометра обычно не превышает 3...4 м.
ОПРЕДЕЛЕНИЕ СИЛЫ И ПОЛОЖЕНИЯ ЦЕНТРА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКИЕ И КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ. ЭПЮРЫ ДАВЛЕНИЙ
Определим силу суммарного гидростатического давления действующего на плоскую прямоугольную фигуру (с проекцией на плоскость чертежа EF) площадью S, расположенную на стенке FO, наклоненной к горизонту под углом а (рис. 2.7 а). Проекцию фигуры EF на плоскость чертежа примем за' ось координат у. Продлим линию EF до пересечения с уровнем свободной поверхности жидкости в точке О, которую будем считать за начало координат. Линия Ох, перпендикулярная направлению EF, будет в нашей системе осью х. Мысленно повернув фигуру EF вокруг оси у до совмещения с плоскостью чертежа, выделим на площади S бесконечно малую полоску шириной dy. Эта полоска, погруженная в жидкость на глубину h, находится на расстоянии у от оси х и имеет элементарную площадку dS.
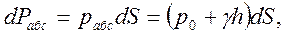
Бесконечно малая сила абсолютного гидростатического давления, действующего на рассматриваемую полоску,
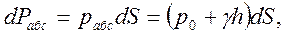
где  — абсолютное гидростатическое давление в области бесконечно малой полоски.
— абсолютное гидростатическое давление в области бесконечно малой полоски.


Рис. Схема определения силы давления:
а—на плоскую стенку; б — на криволинейную поверхность
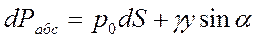
Из треугольника OMN, у которого сторона MN равна h, a сторона NO равна у, находим h=y sin a. Тогда
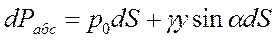
Для определения силы гидростатического давления проинтегрируем это выражение по площади S:
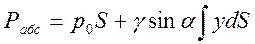
Интеграл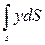 выражает статический момент площади фигуры
выражает статический момент площади фигуры
EF относительно оси х, т. е.  Величину расстояния ус от
Величину расстояния ус от
центра тяжести до оси х находим из треугольника OMcNc 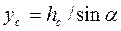 Здесь hс— глубина погружения центра тяжести площадки S в жидкость. Тогда
Здесь hс— глубина погружения центра тяжести площадки S в жидкость. Тогда
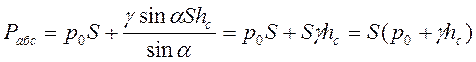
Следовательно, сила полного давления на плоскую фигуру равна абсолютному гидростатическому давлению в центре тяжести этой фигуры P с, умноженному на площадь фигуры S.
В случае, когда Ро=Рат, сила полного давления, действующего на плоскую фигуру, равна произведению площади фигуры на избыточное давление в ее центре тяжести.
Центр давления — точка приложения сил избыточного гидростатического давления 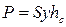 . Для определения ординаты центра давления уц воспользуемся теоремой Вариньона: момент равнодействующей относительно любой оси должен быть равен сумме элементарных моментов составляющих ее сил относительно той же оси, т..
. Для определения ординаты центра давления уц воспользуемся теоремой Вариньона: момент равнодействующей относительно любой оси должен быть равен сумме элементарных моментов составляющих ее сил относительно той же оси, т..  или
или 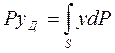
откуда 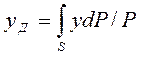
Элементарная сила избыточного давления 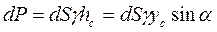 , а равнодействующая этих сил
, а равнодействующая этих сил 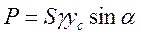 .
.
Тогда значение ординаты центра давления
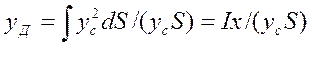
где 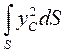 — момент инерции Ix фигуры EF относительно оси х
— момент инерции Ix фигуры EF относительно оси х
Используя для него формулу перехода к оси, проходящей через центр тяжести С, получим
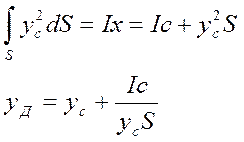
Как видно из рассмотренного, центр давления лежит ниже центра тяжести фигуры на расстоянии эксцентриситета Ic/(yc S).
Графическим изображением изменения гидростатического давления вдоль плоской стенки служат эпюры давления (рис.). Площадь эпюры выражает силу давления, а центр тяжести эпюры — это точка, через которую проходит равнодействующая сила давления.
При построении эпюр учитывают, что давление направлено нормально к стенке, а уравнение Р = Ро + yh, характеризующее распределение гидростатического давления по глубине, является уравнением прямой.
Чтобы построить эпюры давления на вертикальную стенку, откладывают в выбранном масштабе давление по горизонтальному направлению, совпадающему с направлением сил давления (на поверхности жидкости и у дна), соединив концы этих отрезков прямой линией.


Рис. Примеры построения эпюр давления на стенку:
Эпюра абсолютного гидростатического давления представляет собой трапецию, а эпюра избыточного — треугольник (рис. а).
Если плоская стенка, на которую действует жидкость, наклонена к горизонту под углом a (рис. б), то основное уравнение гидростатики принимает следующий вид:
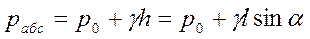
Таким образом, эпюры абсолютного и избыточного гидростатического давления на наклонную стенку представляют собой соответственно наклонную трапецию и наклонный треугольник.
Если плоская стенка, на которую с двух сторон оказывает воздействие жидкость, вертикальна, то на нее будут действовать параллельные и противоположно направленные силы гидростатического давления. Эпюра гидростатического давления на вертикальную стенку представляет собой вертикальную трапецию.
Эпюра гидростатического давления на горизонтальное дно резервуара представляет собой прямоугольник, так как при постоянной глубине избыточное давление на дно постоянно.
На практике широко применяют криволинейные поверхности, находящиеся под давлением жидкости (стенки труб, резервуаров и т. д.).
Рассмотрим действие избыточного гидростатического давления на криволинейную поверхность EF (рис. б). Выделим на этой поверхности элементарную площадку dS, центр тяжести которой погружен в жидкость на глубину h. На эту элементарную площадку будет действовать сила избыточного гидростатического давления 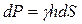 , которую можно разложить на вертикальную и горизонтальную составляющие, т. е. на силы dPz и dPx.
, которую можно разложить на вертикальную и горизонтальную составляющие, т. е. на силы dPz и dPx.
Предположим, что элементарная сила dP наклонена к горизонту под углом a. Тогда составляющие силы dPx и dPz могут быть представлены в виде 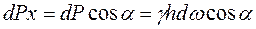 и
и 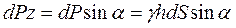
Величина dScosа является проекцией dS на вертикальную плоскость, т. е. 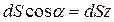 Следовательно,
Следовательно, 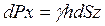 Тогда
Тогда
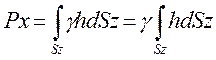 Здесь интеграл
Здесь интеграл 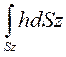
является статическим моментом всей площади вертикальной проекции криволинейной поверхности Sz относительно свободной поверхности жидкости. Этот статический момент равен произведению Sz на глубину погружения центра ее тяжести hc, т. е.
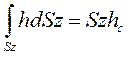
Следовательно, горизонтальная составляющая полной силы избыточного гидростатического давления, действующего на криволинейную поверхность, равна силе гидростатического давления, под воздействием которого находится вертикальная стенка, равная по площади вертикальной проекции рассматриваемой криволинейной поверхности:
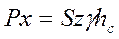
Величина составляющей может быть выражена площадью эпюры гидростатического давления.
Величина dS sinа является проекцией dS на горизонтальную плоскость, т. е. 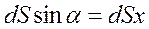
Выражение h dSx представляет собой объем dV призмы. Произведение же yhdSx является весом жидкости в этом бесконечно малом объеме, т. е.
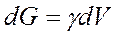
Тогда вертикальная составляющая полной силы избыточного гидростатического давления
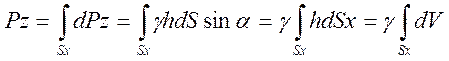
Объем V, являющийся суммой элементарных объемов, называют телом давления. Значит, вертикальная составляющая полной силы избыточного давления, действующего на криволинейную поверхность, равна весу жидкости в объеме тела давления.
Полная сила избыточного гидростатического давления, являющаяся равнодействующей ее составляющих Рх и Рz, определяется зависимостью
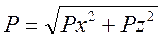
а ее направление — углом a, который можно найти из выражения
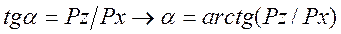
Полная сила избыточного гидростатического давления Р приложена в центре давления. В данном случае центр давления будет расположен в точке пересечения вектора полной силы давления с криволинейной поверхностью EF. Вектор полной силы давления Р должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих под углом a. Центр давления для криволинейных поверхностей находят графоаналитическим методом.



Рис. 1.13. Эпюры давления на плоские прямоугольные стенки:
а- вертикальная стенка; б – наклонная стенка, в – вертикальная стенка с двусторонним действием воды; г – наклонная стенка с двусторонним действием воды; д – стенка в виде ломанной поверхности.
Эпюра давления будет в виде трапеции (рис.). При P о=Pат давление распределяется по закону уравнения первой степени 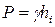 :
:
если 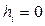 , то
, то 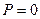
|
Дата добавления: 2014-01-03; Просмотров: 656; Нарушение авторских прав?; Мы поможем в написании вашей работы!