Устойчивость усилителей с обратной связью

Проходная проводимость и ее влияние на входные свойства усилительных схем

Часто усилительный тракт в целом или его отдельное звено организованы таким образом, чтобы в них помимо однонаправленного по передаче усилительного звена K ₀ в присутствует пассивный двухполюсник

Из выражения , определяющего коэффициент усиления линейной системы с ОС в установившемся режиме, следует: при значении петлевого коэффициента усиления 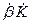=1 коэффициент усиления системы становится бесконечно большим. При этом ничтожно малое входное напряжение частоты, для которой 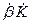=1, должно привести к появлению на выходе бесконечно большого напряжения этой частоты. В действительности выходное напряжение не будет бесконечно большим, ограничиваясь амплитудной характеристикой системы.

Так как на входе любой системы имеется напряжение тепловых и других шумов с непрерывным частотным спектром, то на выходе системы с 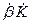=1 даже при отсутствии входного сигнала появляются электрические колебания частоты, для которой петлевое усиление равно единице. Это явление называют самовозбуждением системы.

Самовозбудившаяся система не может усиливать подаваемые на ее вход электрические сигналы, т.к. она оказывается загруженной собственными колебаниями. Поэтому для УУ самовозбуждение недопустимо, и его предотвращение является одной из основных задач проектирования усилителей с ОС.

Устойчивой в отношении самовозбуждения усилительной системой считают такую, которая не может самовозбудиться в эксплуатационных условиях. Ввиду того, что в эксплуатационных условиях коэффициент усиления усилителя и его частотно-фазовая характеристика (ФЧХ) могут изменяться, для обеспечения устойчивости системы необходимо иметь запас как по модулю вектора 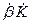, так и по его фазе.

В УУ с ООС введение сколь угодно глубокой ОС казалось бы не может вызвать самовозбуждения, т.к. при этом знаменатель выражения () положителен и превышает единицу. Однако при дополнительном фазовом сдвиге цепи 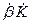на ±π (в этом случае суммарный сдвиг составит либо 2π, либо 0) ООС превращается в положительную и, если при этом 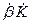=1, устройство самовозбуждается.

Ввиду того, что дополнительный фазовый сдвиг цепи 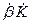достигает π обычно за пределами рабочей полосы частот, самовозбуждение усилителя с ООС обычно имеет место на очень низких или очень высоких частотах, выходящих за пределы рабочей полосы частот.

Расчет устойчивости выполняется на основе так называемых критериев устойчивости. Наиболее удобным для расчета устойчивости усилителей является критерий Найквиста.

Критерий Найквиста для однопетлевой ОС формируется так. Если полярная диаграмма вектора 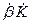, представляющая собой геометрическое место точек, соответствующих перемещению конца этого вектора при изменении частоты от 0 до ∞, не охватывает критической точки с координатами (+1; j 0), то система устойчива. Если указанная точка находится внутри контура полярной диаграммы, то система неустойчива, и возникает генерация. Контур полярной диаграммы называют также годографом вектора .

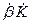На точка с координатами (1; 0) лежит внутри годографа вектора 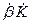для диапазона частот от 0 до ∞, и поэтому система неустойчива, т.к. для частоты, соответствующей пересечению годографа с горизонтальной осью правее точки (1; 0), произведение 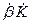вещественно и превышает единицу, а, следовательно, для этой частоты выполняется условие самовозбуждения.

Рис.... Полярная диаграмма вектора K β_ос

как видно из рис...., точка с координатами (1; 0) лежит вне указанного годографа, а значит система с ОС устойчива, т.к. частота, для которой выполняется условие самовозбуждения, не существует.

Получение устойчивой работы усилителя с ООС встречает тем больше трудности, чем больше глубина ОС γ₀=1+ K ₀β₀ и чем больше число каскадов ею охватывается. Это объясняется тем, что при большой величине глубины ОС на средней частоте γ₀ для создания необходимых запасов устойчивости по усилению требуется большая крутизна его спадания, приводящая к резкому изменению (φ _K +φ_β). В то же время необходимые запасы устойчивости по мере увеличения числа каскадов, естественно, возрастают.

За пределами области СЧ петлевой коэффициент усиления K β=γ−1 перестает сохранять вещественное значение, фаза напряжения ОС начинает изменяться и действие ОС, направленное на уменьшение искажений и стабилизацию характеристик усилителя, пропадает. При достаточно больших фазовых сдвигах в цепях усилителя или ОС на определенных частотах ОС становится положительной (γ<1) и это может приводить к резкому увеличению искажений сигнала и нестабильности основных параметров усилителя, а в худшем случае – к самовозбуждению усилителя.

Из (4-*) следует, что самовозбуждение (K_{E ос}→∞) наступает при условии γ=0, т.е. K β=−1. На практике для предотвращения самовозбуждения выполняют условие

(4-*)

на частоте, при которой наступает баланс фаз:

. (4-*)

С точки зрения общей формулировки критерия устойчивости Найквиста требуется, чтобы АФХ коэффициента петлевого усиления (рис. 4.*) построенная для частот от 0 до ∞, не охватывала точку –1 на вещественной оси (например, рис. 4.*, а). Эта формулировка позволяет считать устойчивыми системы с характеристикой типа показанной на рис. 4.*, в, которая не удовлетворяет условиям (4-*) и (4-*). Подобные системы называют условно устойчивыми, поскольку при уменьшении коэффициента усиления (например, при снижении температуры окружающей среды) они теряют устойчивость. В усилителях всегда требуют абсолютной устойчивости и поэтому пользуются критерием (4-*).

Рис. 4.*. Диаграммы Найквиста для петлевого коэффициента усиления усилителя: абсолютно устойчивого усилителя (а), неустойчивого (б) и условно устойчивого (в); определение запаса устойчивости (г).

Выражение (4-*) при подстановке в него γ=0 (K β=−1) показывает, что условием неустойчивости можно считать также взаимную компенсацию реактивных и активных составляющих иммитансов W _г и W _вх (или W _н и W _вых). Поскольку активная составляющая W _г (или W _н) положительна, признаком опасности неустойчивости является отрицательный знак активной составляющей W _вх (или W _вых).

На практике требуется определенный запас устойчивости, т.е. удаленность от условий самовозбуждения, гарантирующая отсутствие самовозбуждения при некоторой нестабильности характеристики усилителя. Для этого вводят представление о коэффициенте устойчивости, под которым понимают значение глубины ОС на частоте баланса фаз, т.е.

,

где ω_φ –частота, при которой выполняется условие (4-*), и о запасе по фазе

,

где φ(ω_ср)=φ_K+φ_β – фаза петлевого коэффициента усиления на частоте «среза» ω_ср, при которой выполняется условие баланса амплитуд | K β|=1 (рис. 4.*, г).

Обычно требуют k _у≥0,5…0,8 или φ_зап=20…60°, причем для выполнения этих требований в усилителях с глубокой общей ОС приходится весьма тщательно рассчитывать все частотно-зависимые его цепи в полосе частот, намного превышающей рабочую (стр.*, [*]).

Дата добавления: 2014-01-03