Усилительный каскад с последовательной ООС по току

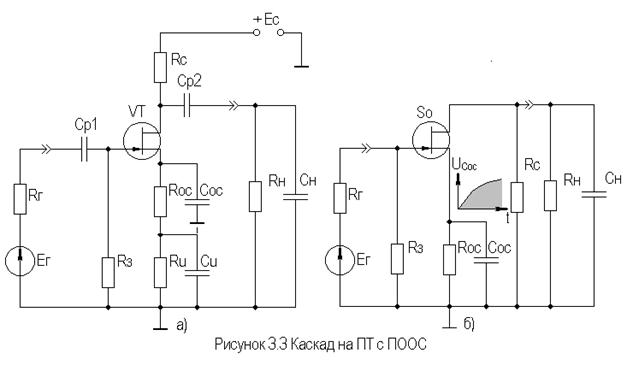
Схема каскада с последовательной ООС по току (ПООСТ) на ПТ с ОИ приведена на рис. 3.3.

При ПООСТ в выходной цепи усилителя последовательно с нагрузкой включается специальная цепь (на рис. 3.3 это 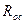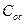), напряжение на которой 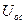пропорционально выходному току. Во входной цепи усилителя 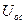алгебраически складывается с входным напряжением.

В области СЧ (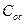=0) можно записать

.

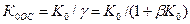Проведя анализ каскада по методике подраздела 2.3, получим:

.

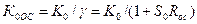Поскольку 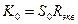(см. подразд.?.?), то при глубокой ООС (γ>10) 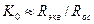. Из полученного выражения следует, что ПООСТ обеспечивает стабильность усиления по напряжению при условии постоянства нагрузки.

С помощью ПООСТ удается уменьшить нелинейные искажения в УУ, поскольку с увеличением γ будет уменьшаться напряжение управления усилителем, его работа станет осуществляться на меньшем участке ВАХ активного элемента (транзистора), а это приведет к уменьшению коэффициента гармоник. В подразд.?.? приведены расчетные соотношения для коэффициента гармоник усилителя, охваченного ООС последовательного типа. Приближенно оценить влияние ПООСТ на коэффициент гармоник можно по соотношению:

.

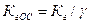Все вышесказанное в равной мере относится и к каскаду на БТ с ОЭ и ПООСТ (схема каскада не приводится ввиду идентичности ее топологии схеме рис. 3.3).

Входное сопротивление усилителя с ООС определяется способом подачи напряжения ОС во входную цепь. Согласно элементарной теории ОС, ПООСТ увеличивает входное сопротивление усилителя в γ раз, т.е.

.

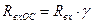Выражение для входного сопротивления каскада с ОЭ на БТ с ПООСТ, определенное по методике подразд. 2.3, имеет вид:

.

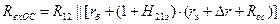При известных допущениях последние два выражения дают близкие результаты.

Входное сопротивление каскада с ОИ на ПТ определяется 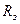(см. подразд.?.?), поэтому практически не меняется при охвате каскада ПООСТ.

Выходное сопротивление усилителя с ООС определяется способом снятия напряжения ОС с нагрузки усилителя. Согласно элементарной теории ОС, ПООСТ увеличивает выходное сопротивление усилителя в γ раз, т.е.

.

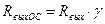На СЧ выходное сопротивление каскадов на ПТ (ОИ) и БТ (ОЭ) определяется в большинстве случаев соответственно номиналам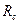и и 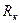, поэтому данная ООС его практически не меняет.

На рис. 3.3 б приведена схема каскада с ОИ и ПООСТ в области ВЧ. Данный каскад еще носит название каскада с истоковой коррекцией, т.к. основной целью введения в каскад ООС является коррекция АЧХ в области ВЧ.

Поскольку цепь ООС (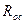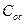) частотнозависима, то |γ| с ростом частоты уменьшается относительно своего значения на СЧ, что приводит к относительному возрастанию 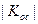на ВЧ. С точки зрения коррекции временных характеристик, уменьшение 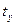каскада объясняется зарядом 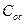, что приводит к медленному нарастанию 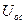, и, следовательно, к увеличению коэффициента усиления в области МВ, а это, в свою очередь, сокращает время заряда 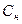, которое, собственно, и определяет .

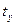Анализ влияния ПООСТ вначале проведем для случая резистивной цепи ОС (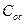=0). Учитывая, что крутизна ПТ практически не зависит от частоты (см. подразд.?.?.?), можно сказать, что во всем диапазоне рабочих частот глубина ООС γ=const, уменьшение коэффициента усиления по всему диапазону рабочих часто одинаково и коррекция отсутствует.

Воспользовавшись рекомендациями подразд.?.?, получим выражение для комплексного коэффициента передачи каскада с токовой коррекцией (цепь ОС комплексная, 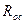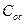) на ВЧ:

,

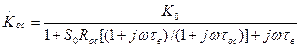где .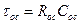

Анализ полученного выражения упрощается в предположении 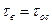. При этом условии имеем:

,

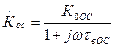где 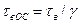(см. так же подразд.?.?).

Уменьшение постоянной времени каскада в области ВЧ приводит к увеличению верхней граничной частоты 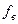(уменьшению 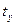) каскада. Площадь усиления каскада с ОИ и истоковой коррекцией при этом не меняется:

.

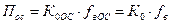Расчет каскада с истоковой коррекцией в области НЧ ничем не отличается от расчета некорректированного каскада за исключением того, что формула для постоянной времени цепи истока будет выглядеть иначе:

.

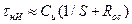В зависимости от цели введения ООС в каскад, глубину ООС можно определить по следующим соотношениям:

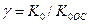, либо .

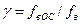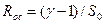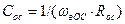При этом и . Каскад с ОЭ и ПООСТ еще носит название каскада с эмиттерной коррекцией.

В отличие от ПТ, в БТ крутизна частотнозависима, поэтому даже при частотно-независимой цепи ООС (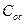=0) наблюдается эффект коррекции АЧХ и ПХ за счет уменьшения глубины ООС на ВЧ:

,

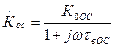где 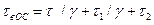(см. так же подразд. 2.5).

Нетрудно увидеть, что эмиттерная коррекция каскада на БТ при частотно-независимой цепи ООС (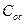=0) эффективна при 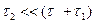, т.е. в каскадах с малой емкостью нагрузки.

Воспользовавшись рекомендациями подразд.?.?, получим выражение для комплексного коэффициента передачи каскада с эмиттерной коррекцией в области ВЧ:

,

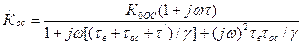где , .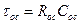

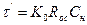Эмиттерная коррекция позволяет значительно увеличить 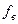(уменьшить 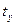) при заданных величинах подъема АЧХ на ВЧ (выброса ПХ d в области МВ). Готовые таблицы и графики для расчета каскада с эмиттерной коррекцией приведены в [?].

Входная емкость каскада с ПООСТ уменьшиться примерно в γ раз:

.

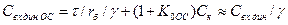Расчет каскада с ОЭ и ПООСТ в области НЧ ничем не отличается от каскада без ОС (следует только учитывать изменение при расчете постоянных времени разделительных цепей), исключение составляет расчет постоянной времени цепи эмиттера:

.

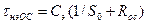Дата добавления: 2014-01-03