Виды средних величин. В зависимости от исходных данных рассчитывается несколько видов степенных средних величин

В зависимости от исходных данных рассчитывается несколько видов степенных средних величин. Они могут быть рассчитаны по сгруппированному и не сгруппированному признаку (соответственно различают простые и взвешенные средние величины).

В каждом конкретном случае для определения исходного соотношения средней может использоваться одна из следующих форм средних величин:

1)средняя арифметическая;

2)средняя хронологическая;

3)средняя геометрическая;

4)средняя гармоническая;

5)средняя квадратическая;

6)средняя кубическая и т.д.

Все степенные средние величины сроятся по одному общему принципу:

где – варианта;

n=N – объем статистической совокупности;

k – показатель степени.

Показатель степени k может принимать любые значения. На практике обычно используются несколько его значений:

при k=1 получают среднюю арифметическую;

при k=-1 получают среднюю гармоническую;

при k=0 получают среднюю геометрическую;

при k=2 получают среднюю квадратическую.

Все степенные средние различаются между собой значениями показателя степени. При этом чем выше показатель степени, тем больше количественное значение среднего показателя.

.

Данное свойство степенных средних называется свойством мажорантности средних.

Средняя арифметическая является наиболее распространённым видом средних величин, может быть простой или взвешенной.

Средняя арифметическая простая используется в тех случаях, когда расчёт осуществляется по несгруппированным данным.

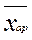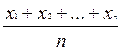==, где

х - значение показателя;

n - количество показателей

Пример: сотрудники бригады имеют следующий стаж работы:

Табельный номер рабочего
Стаж (лет)

Определить средний стаж.

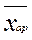=57/78,1 года

При расчёте средних величин, отдельные значения осредняемого признака по совокупности могут повторяться (встречаться по несколько раз). В данном случае расчёт средней производится по сгруппированным данным или вариационным рядам. При этом для расчета используют формулу средней арифметической взвешенной. По средней арифметической взвешенной рассчитывается среднесписочное число сотрудников, средние доходы, цены и т.д.

Зависимость для определения средней арифметической взвешенной для дискретного вариационного ряда будет иметь следующий вид:

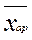=, где

х - значение признака;

f - частота (вес) i-того признака

Пример: по исходным данным дискретного вариационного ряда рассчитать среднюю арифметическую взвешенную.

Пример: продажа акций на торгах условной фондовой биржи:

Сделка	Количество проданных акций, шт. fi	Курс продажи акций, руб. xi

=

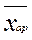При расчете средней арифметической по интервальному вариационному ряду для выполнения вычислений от интервалов переходят к их серединам.

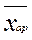=, где

- середина i-того интервала;

f - частота (вес).

Средняя арифметическая обладает рядом полезных свойств, важнейшими из которых являются:

1. Средняя арифметическая постоянной величины равна этой величине.

2. Алгебраическая сумма отклонений вариант от их средней арифметической равна нулю.

3. Если все варианты увеличить (уменьшить) на постоянное число А, то средняя арифметическая увеличится (уменьшится) на это же число.

4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз.

5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится.

Средняя хронологическая – исчисляется в том случае, когда данные представлены в хронологическом порядке. По этой средней рассчитывают средние товарные запасы, средние остатки готовой продукции на складе.

=

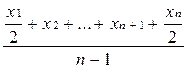
Средняя гармоническая исчисляется, когда известно общее значение признака и индивидуальные значения, связанные с этим признаком.

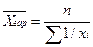-по не сгруппированному признаку

-по сгруппированному признаку

где W_i = x_i*f_i (W_i –статистический вес).

Средняя геометрическая применяется в тех случаях, когда общий объём осредняемого признака является мультипликативной величиной, т.е. определяется умножением отдельных значений признака.

- средняя геометрическая простая

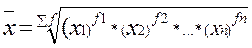- средняя геометрическая взвешенная

Наибольшее распространение средняя геометрическая получила в анализе рядов динамики.

Средняя квадратическая – используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин.

Средняя квадратическая применяется для измерения степени колеблемости индивидуальных значений признака относительно средней арифметической, а также в тех случаях, когда необходимо вычислить среднюю величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины участков, диаметра труб, стволов и т.д.).

- простая

- взвешенная.

Дата добавления: 2014-01-03