Абсолютные показатели вариации

Понятие вариации

Тема 5. Показатели вариации

1. Понятие вариации

2. Абсолютные показатели вариации

3. Относительные показатели вариации

4. Виды дисперсий и правило их сложения

5. Эмпирическое корреляционное отношение

Вариация – это колеблемость значения признака от его среднего значения.

Чем больше мера колеблемости, тем неоднороднее совокупность, тем неистиннее средняя величина.

Средняя величина представляет собой обобщающую статистическую характеристику, в которой получает количественное выражение типичный уровень признака, которым обладают показатели изучаемой статистической совокупности. Однако, средняя величина не позволяет учесть все характерные черты статистического распределения. Для характеристики и упорядочения статистических совокупностей используют показатели вариации.

К абсолютным показателям вариации относят:

-размах вариации;

-среднее линейное отклонение;

-дисперсия;

-среднее квадратическое отклонение.

Размах вариации представляет собой разброс элементов совокупности.

R = x_max – x_min

Данный показатель учитывает только крайнее значение признака совокупности и, следовательно, не отражает отклонение всех вариантов значения признака.

Среднее линейное отклонение учитывает различие всех единиц изучаемой совокупности. Оно представляет собой среднюю арифметическую абсолютных значений отклонений отдельных значений признака от их средней арифметической.

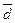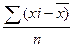= - для несгруппированных данных;

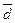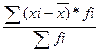= - для сгруппированных данных.

В практических расчётах среднее линейное отклонение используется для оценки ритмичности производства, равномерности поставок.

Дисперсия представляет собой средний квадрат отклонений значений признака от их средней величины.

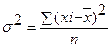- для несгруппированных данных;

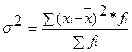- для сгруппированных данных.

При расчёте дисперсии в интервальных рядах распределения в качестве вариантов значений признака используется середина интервала; в результате получается приближенное значение дисперсии.

Показатель дисперсии обладает рядом вычислительных свойств, позволяющих упростить её расчёт.

Свойства дисперсии:

1)Дисперсия постоянной величины равна нулю.

2)Дисперсия не меняется, если все варианты увеличиваются или уменьшаются на одно и то же число.

3)Если все варианты признака умножить (разделить) на число а, то дисперсия увеличится (уменьшится) в а² раз.

Размерность дисперсии соответствует квадрату размерности исследуемого признака, поэтому для сохранения экономического смысла будет рассчитываться показатель, который называется средним квадратическим отклонением.

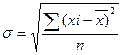- для несгруппированных данных;

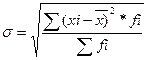- для сгруппированных данных.

Среднее квадратическое отклонение имеет размерность осредняемого признака. Этот показатель используется для оценки надёжности средней величины. Чем меньше среднее квадратическое отклонение, тем надёжнее среднее значение признака, и тем лучше средняя величина представляет исследуемую статистическую совокупность.

Дата добавления: 2014-01-03