Вычисление линейных невязок по осям координат

Вычисление приращений координат

Вычисление дирекционных углов и румбов.

По исходному дирекционному углу α_пт–I и исправленным значениям углов определяют дирекционные углы сторон теодолитного хода:

α_n=α_n–1±180º–β_n – для правых углов

α_n=α_n–1±180º+β_n – для левых углов

Контролем правильности вычислений дирекционных углов является совпадение значения дирекционного угла начальной стороны α_I–II:

α_I–II= α_пт–1±180º–β_пр=α_V–I±180º–β₁

Вычисляют румбы

№ четв.	Дирекционный угол	Назв. румба	Формулы	Знаки приращения
∆x	∆y
I	0 º–90º	СВ	r= α	+	+
II	90º–180º	ЮВ	r=180º –α	–	+
III	180º–270º	ЮЗ	r= α– 180º	–	–
IV	270º–360º	СЗ	r=360º– α	+	–

По значениям дирекционных углов и горизонтальными проложениям сторон теодолитного хода вычисляют приращения координат с точностью до 0.01м:

∆х=d·cos r

∆у=d·sin r

Знаки приращения координат определяют в зависимости от названия румба.

Находят суммы вычисленных приращений

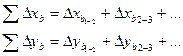
И теоретические суммы приращений

ΣΔх_т=х_кон–х_нач

ΣΔу_т=у_кон–у_нач

Линейные невязки по осям координат

f_x= Σ∆х_ф– Σ∆х_т

f_у= Σ∆у_ф–Σ∆у_т

Вычисление абсолютной и относительной невязок теодолитного хода

f_абс =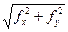

Определяют относительную линейную невязку f_отн теодолитного хода: f_отн=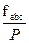

где Р – периметр хода.

Допустимое значение относительной невязки не должно превышать погрешности линейных измерений 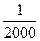. Если это условие нарушено, то длины линий перемеряют, а если выполняется, то вычисляют поправки в вычисления координат:

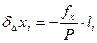
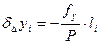
Поправки округляют до 0.01 мм и выписывают их со своими знаками над соответствующими приращениям ∆х и ∆у.

Сумма поправок должна равняться невязке с обратным знаком:

Σδ_Δx=–f_x

Σδ_Δy=–f_y

Вычисляют исправленные приращения координат и записывают результаты в ведомость:

∆х_испр= ∆х_{выч +} δ_Δх

∆у_испр= ∆у_{выч +} δ_Δу

Для контроля определяют суммы исправленных приращений координат, которые должны быть равны теоретическим суммам приращений:

∆х_испр= Σх_т

∆у_испр= Σу_т

Дата добавления: 2014-01-03