Полиномиальная формула и формула бинома

Пусть требуется вычислить выражение 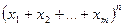, т.е. перемножив n скобок, привести его к виду

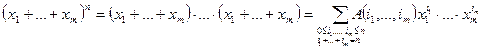
Числа 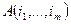называются полиномиальными коэффициентами. Найдем эти числа. В соответствии с правилами алгебры из каждой скобки выбирается один из символов 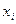и они перемножаются. Коэффициенты 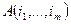получаются в результате приведения подобных членов в полученной таким образом сумме произведений. Таким образом коэффициент 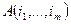равен числу последовательностей длины n, составленных из символов 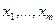, причем символ 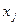используется 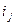раз. В соответствии с 1.1 число таких последовательностей равно 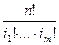. Это дает полиномиальную формулу: .

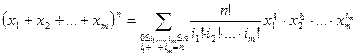В частном случае, когда в n- ую степень возводится двучлен, она используется наиболее часто и называется биномом Ньютона

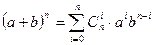
Из школьного курса математики известны частные случаи этой формулы при n=2 и n=3.

Приведем важнейшие тождества для биномиальных коэффициентов

1. ;

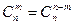2. ;

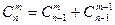3. ;

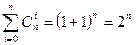4. ;

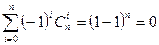5. ;

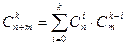6. .

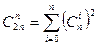Тождество 1 уже известно. Тождество 2 можно получить с помощью следующего рассуждения. Выделим в 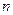- элементном множестве один из элементов. Каждое 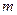- элементное подмножество либо содержит, либо не содержит выделенный элемент. Подмножеств первого типа 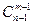, второго - .

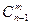Третье и четвертое тождества следуют, как это показано, из формулы бинома, причем третье тождество выражает тот факт, что n- элементное множество имеет 2ⁿ подмножеств. Пятое тождество получим, если рассмотрим разбиение 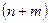- элементного множества на 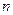- элементное и 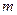- элементное. Шестое тождество следует из пятого, если положить.

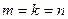Отметим, что биномиальные коэффициенты 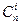растут по i от 0 до [i/2] и убывают от ] i/2 [ до n. При n- четном максимальный коэффициент один -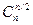, при n- нечетном максимальных коэффициентов два - 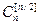и .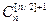

При больших n биномиальные коэффициенты могут быть оценены с помощью асимптотической формулы Стирлинга

, .

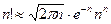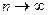Тест

1. Коэффициент при 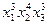в разложении (x₁+x₂+x₃)¹⁰ равен а) 10³; б) 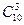; в) .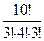

2. Коэффициент при а³b³с⁴ в разложении 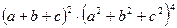равен а)12; б) 24; в) 18.

3. Коэффициент при t¹⁷ в разложении 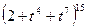равен а)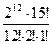; б) 0; в) .

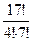Дата добавления: 2014-01-03