И теорема Пойа

Перечисление в присутствии группы. Лемма Бернсайда

Рассмотрим задачу о числе раскрасок граней куба в 3 цвета: белый (white), синий (blue) и красный (red). Так как есть три возможности для раскраски каждой из 6 граней, то всего раскрасок 3⁶=729. Далее, можно найти число раскрасок, использующих i раз белый, j раз синий и k раз красный цвет (i+j+k=6). Для этого достаточно раскрыть 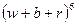с помощью полиномиальной формулы

.

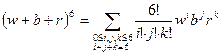При этом фактически каждой грани куба ставится в соответствие скобка 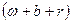, и выбор цвета при раскраске грани соответствует выбору буквы при раскрытии скобок. Таким образом, раскрасок, использующих i раз белый, j раз синий и k раз красный цвет, имеется

.

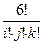Эти формулы, однако, справедливы лишь в том случае, если все грани куба различны, другими словами, куб занимает определенное положение в пространстве. Если же куб можно поворачивать, самосовмещая его, то различные раскраски могут переходить друг в друга, совмещаться. При этом естественно считать совместимые раскраски одинаковыми и ставить задачу нахождения числа различных раскрасок. На математическом языке это можно выразить следующим образом. Группа самосовмещающих вращений куба действует как группа перестановок на множестве из 3ⁿ раскрашенных кубов. Совместимость различных раскрасок является отношением эквивалентности. Классы эквивалентности принято называть в данном случае орбитами. Таким образом, требуется найти число орбит, а также число орбит, раскраски которых используют заданное число раз каждый из цветов.

Сформулируем общий результат о числе орбит, возникающих при действии группы на конечном множестве, выражаемый леммой Бернсайда. Пусть группа G действует на конечном множестве Х, элементы которого будем называть точками. Результат действия элемента группы 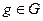на точку 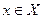будем обозначать через 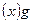, т.е. писать точку в скобках слева от действующего на нее элемента группы. Точку 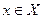назовем стационарной для элемента 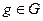, если 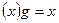. Через X_g обозначим множество стационарных для 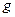точек. 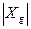и 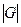- число элементов множества 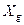и группы .

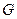Лемма Бернсайда. Число орбит N при действии группы G на конечном множестве точек X равно среднему по группе числу стационарных точек

.

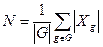Доказательство. Пусть 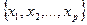- одна из орбит при действии G на X. Пусть A_i – множество элементов 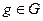таких, что 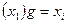, 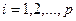. Тогда 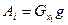где 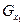- стабилизатор точки 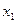, т.е. такая подгруппа группы G, элементы которой оставляют на месте точку 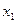, а 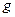– произвольный фиксированный элемент множества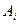. В самом деле, ясно что 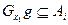. Докажем обратное включение. Пусть 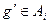, т.е. 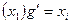. Тогда 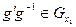, т.к. 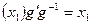. Поэтому 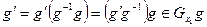. Этим доказывается, что 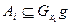,т.е. 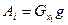. Таким образом. 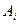, 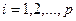- множество смежных классов по стабилизатору 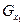. По теореме Лагранжа

;

;

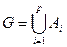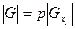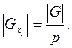
Такую же мощность имеют и стабилизаторы остальных точек орбиты

, .

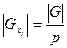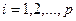Поэтому .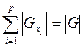

Рассмотрим теперь двудольный граф, одну долю которого составляют элементы группы G, другую – точки множества X. Ребро (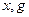) проводится в таком и только в том случае, если точка 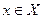является стационарной для элемента .

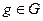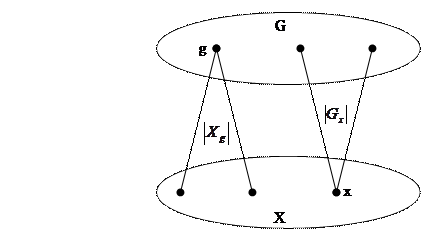
Подсчитаем теперь число ребер графа двумя способами: с верхней доли и с нижней доли. С верхней доли подсчет дает

.

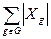С нижней доли подсчет дает

.

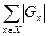Если последнюю сумму разбить по орбитам, то вклад каждой орбиты по доказанному ранее будет равен 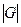. Поэтому вся сумма будет равна 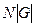, где N - число орбит. Имеем

.

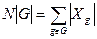Откуда

.

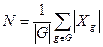Лемма доказана.

Вернемся теперь к задаче о раскраске граней куба. С этой целью рассмотрим группу самосовмещающих вращений куба. Так как куб можно поставить на стол любой из 6 своих граней и при этом имеется ещё 4 самосовмещающих положения, то эта группа содержит 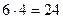элемента, а именно:

1. Тождественное вращение.

2. 3 нетождественных вращения вокруг каждой из 3 осей, соединяющих середины противоположных граней, - итого 9 вращений.

3. 2 нетождественных вращения вокруг каждой из 4 осей, соединяющих противоположные вершины, - итого 8 вращений.

4. 1 нетождественное вращение вокруг каждой из 6 осей, соединяющих середины противоположных ребер, - итого 6 вращений.

Выпишем циклическую структуру каждого из вращений как перестановки на множестве 6 граней.

1. Тождественное вращение оставляет каждую из 6 граней на месте. Запишем это как 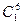(6 циклов длины 1).

2. Эти вращения по циклической структуре разбиваются на 2 класса: вращения на 180⁰ и вращения на 90⁰. Первые имеют циклическую структуру 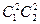(2 цикла длина 1 и 2 цикла длины 2), вторые - 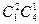(2 цикла длины 1 и 1 цикл длины 4).

3. Эти вращения имеют циклическую структуру 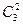(2 цикла длины 3).

4. Это вращение имеет циклическую структуру 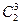(3 цикла длины 2).

Просуммировав циклические структуры всех перестановок и поделив сумму на число элементов в группе, получим так называемый цикловой индекс группы

.

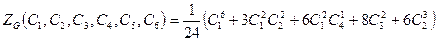Зная цикловой индекс группы самосовмещений куба и опираясь на лемму Бернсайда, легко найти число орбит действия этой группы на множестве 3⁶ раскрасок. Основным здесь является следующее наблюдение. Для данной перестановки 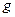граней куба раскраска будет стационарной в том и только в том случае, если грани, принадлежащие одному циклу, выкрашены в один цвет. Поэтому, если циклическая структура перестановки g есть 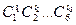и используются 3 цвета, то

.

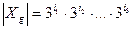Таким образом, для того, чтобы найти число орбит N достаточно согласно лемме Бернсайда в цикловой индекс вместо каждой из переменных 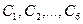подставить число 3:

.

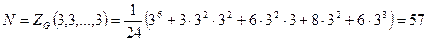А для того, чтобы найти число орбит, раскраски которых используют i раз белый, j раз синий и k раз красный цвет, нужно в цикловой индекс вместо каждой переменной 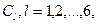подставить 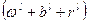и, раскрыв скобки в выражении

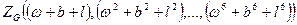, найти коэффициент при 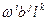. Это и составляет содержание теоремы Пойа. Доказательство повторяет доказательство леммы Бернсайда. Нужно лишь ребрам, отходящим от раскрасок типа 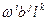, приписать веса, также равные 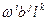, и просуммировать веса ребер двумя способами.

В качестве примера найдем число раскрасок, использующих каждый цвет дважды. Коэффициент, получающийся при 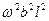после раскрытия скобок в выражении

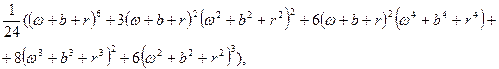
равен

,

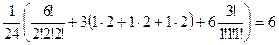что и дает число искомых раскрасок.

Тест

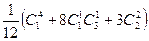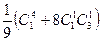1. Цикловой индекс группы самосовмещающих вращений тетраэдра, действующей на множестве его 4 граней, равен а) ; б) ; в) ;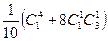

2. Число различных раскрасок граней тетраэдра в 2 цвета с учетом самосовмещений равно а) 5; б) 7; в) 4.

3. Число различных раскрасок граней тетраэдра в 2 цвета, использующих каждый цвет дважды, с учетом самосовмещений равно а) 1; б) 2; в) 3.

Глава II. Графы и алгоритмы.

Дата добавления: 2014-01-03