Паросочетания в двудольных графах

Подмножество М ребер графа G=(V,E) называется паросочетанием, если никакие два ребра из М не имеют общей вершины. Паросочетание называется наибольшим, если оно содержит максимально возможное число ребер. Если наибольшее паросочетание покрывает все вершины графа, то оно называется совершенным. Задача о паросочетании состоит в нахождении наибольшего паросочетания.

Особенно часто она возникает для двудольных графов, множество вершин которых разбивается на 2 непересекающихся подмножества 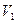и 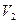, а любое ребро имеет одним своим концом вершину из 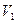, а другим – из 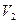. Задача имеет многочисленные интерпретации и приложения. Укажем некоторые из них.

Если 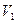- множество юношей, 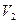- множество девушек, желающих вступить в брак, а ребро в графе соответствует взаимному согласию к вступлению в брак, то задача о паросочетаниях является задачей о заключении максимального числа счастливых браков.

Если 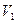- множество лиц, желающих получить работу, 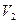- множество вакантных мест, и ребро в графе обозначает способность определенного лица выполнить данную работу, то задача о паросочетании становится задачей о трудоустройстве.

Множество может быть также множеством подмножеств некоторого множества, а - множеством элементов этого же множества. Ребро в этом случае соответствует вхождению элемента в подмножество. Тогда задача о паросочетании становится задачей о выборе различных представителей. Пусть, например, в Думе имеется ряд комитетов, причем член Думы может состоять в нескольких комитетах, но возглавлять не более одного. Тогда задачу выбора председателя в каждом комитете можно рассматривать как задачу о системе различных представителей.

Универсальным подходом, позволяющим строить эффективные алгоритмы для задачи о паросочетании, является подход, основанный на идее чередующейся цепи. Пусть в графе имеется некоторое паросочетание. Если удастся найти цепь, первая и последняя вершина которой не покрыты паросочетанием, а ребра чередуются, попеременно то не входя, то входя в паросочетание, то мощность паросочетания можно нарастить на единицу. Для этого достаточно все ребра цепи, не входящие в паросочетание, включить в него, а все входящие в паросочетание ребра – исключить из паросочетания.

Следующий рисунок, где жирно отмеченные ребра принадлежат паросочетанию, иллюстрирует принцип чередующейся цепи.

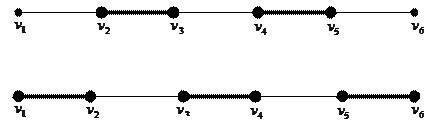
Замечательно, что верно и обратное. Если паросочетание не является наибольшим, то всегда найдется чередующаяся цепь, позволяющая его нарастить. Пусть 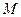– не наибольшее паросочетание, т.е. существует паросочетание 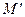такое, что 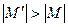. Рассмотрим подграф 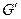графа 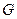, образованный ребрами, входящими ровно в одно из паросочетани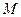й или 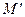. Степень любой вершины графа 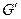не превышает двух. Поэтому каждая компонента связности является циклом или цепью, в которых чередуются ребра двух паросочетаний. Поэтому все циклы имеют четную длину и содержат одинаковые число ребер каждого из паросочетаний. А так как 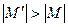, то должна найтись чередующаяся цепь, имеющая больше ребер из паросочетания 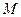, которая и позволяет нарастить паросочетание .

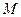Рассмотрим метод чередующейся цепи на примере двудольного графа

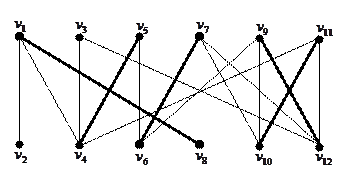
Заданное паросочетание является максимальным в том смысле, что к нему нельзя добавить ни одного ребра. Является ли оно наибольшим? Не покрыты паросочетанием две вершины графа 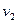и 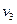. Они находятся в разных долях, но не соединены ребром. Попытаемся найти чередующийся путь из 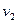в 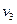. Таким путем является например, 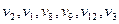. Альтернируя ребра пути, получаем паросочетание, имеющее на одно ребро больше. Оно является совершенным и поэтому наибольшим.

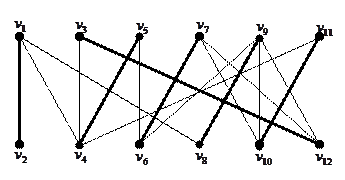
Поиск чередующегося пути занимает в двудольном графе 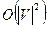операций. Для построения наибольшего паросочетания его нужно применить 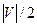раз. Поэтому трудоемкость построения наибольшего паросочетания методом чередующейся цепи есть 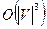операций.

Обратимся теперь к задаче о системе различных представителей и укажем критерий её существования. Пусть 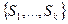- система подмножеств конечного множества 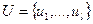. Ясно, что необходимым условием существования системы различных представителей является 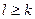, а также, чтобы объединение любых m подмножеств 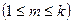имело мощность не менее m. Оказывается, что это условие является и достаточным.

Теорема. (Hall, 1935). Для существования системы различных представителей для системы подмножеств 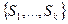конечного множества необходимо и достаточно, чтобы для любых m подмножеств 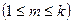выполнялось условие

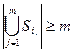
Доказательство. Необходимость очевидна. Для доказательства достаточности воспользуемся интерпретацией системы подмножеств в виде двудольного графа, верхняя доля которого соответствует подмножествам, а нижняя – элементам. Будем последовательно произвольно выбирать представителей для подмножеств 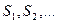до тех пор, пока дойдя до подмножества 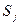не окажется, что все его элементы уже использованы в качестве представителей.

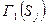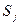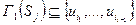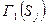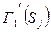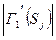
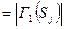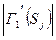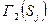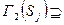
Обозначим через - множество вершин, смежных с вершиной , . Поднявшись по ребрам паросочетания из множества , получим, множество вершин верхней доли , . Из множества , опустившись по всем ребрам графа, получим множество , 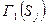. Поднявшись из множества 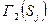по ребрам паросочетания получим множество 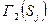и т.д. Каждый раз имеем 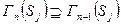. Поэтому априори возможны два исхода. Либо на некотором шаге 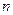множество 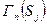выйдет за пределы множества 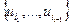, либо стабилизируется, оставшись в пределах множества 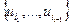, т.е. будет иметь место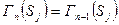 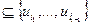. В первом случае возникает чередующаяся цепь, паросочетание наращивается на единицу, и подмножество 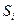получает своего представителя. Во втором случае получается, что множество подмножеств 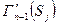имеет в совокупности число элементов, равное числу подмножеств. Если к множеству подмножеств 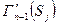добавить множество 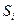, то суммарное число элементов в них не изменится и будет на единицу меньше числа подмножеств, что противоречит условию теоремы. Поэтому этот случай невозможен, и мощность паросочетания можно нарастить на l, и все подмножества получат своих представителей.

Следствие. Регулярный двудольный граф имеет совершенное паросочетание.

Доказательство. Интерпретируя граф как систему подмножеств, покажем, что для нее выполнены условия теоремы Холла, и стало быть, существует система различных представителей, определяющая в графе совершенное паросочетание.

Нужно показать, что для любых m вершин верхней доли графа (подмножеств) для числа 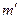смежных им вершин нижней доли (элементов) справедливо неравенство 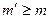. Для этого подсчитаем число соединяющих их ребер двумя способами: сверху и снизу. Если степень графа равна 2, то число этих ребер равно 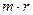, как показывает их подсчет сверху. С другой стороны, это число равно 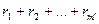, где 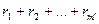- число ребер из выделенного множества, отходящих от каждой из 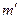вершин нижней доли. Имеем

,

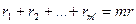а так как 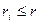, , 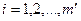то отсюда следует, что .

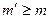Сходным приемом может быть доказана имеющая важное значение в дискретной математике так называемая лемма Шпернера о максимально возможном числе попарно несравниваемых подмножеств данного конечного множества, т.е. таких подмножеств, что ни для какой пары из них не имеет место отношение включения.

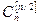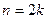Теорема. ( Sperner, 1928). Максимальное число попарно несравнимых подмножеств n – элементного множества равно . При максимальная система подмножеств единственна – это система всех k – элементных подмножеств. При 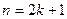максимальных систем две – система всех k – элементных подмножеств и система всех k+1 – элементных подмножеств.

Доказательство. Пусть 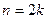. Допустим, что имеется некоторая система попарно несравнимых подмножеств, некоторые из которых имеют мощность, отличную от k. Покажем, что она не может быть максимальной. Пусть, например, минимальная мощность подмножеств системы равна 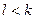. Для каждого подмножества мощности 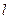рассмотрим 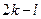содержащих его подмножеств мощности 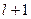. Покажем, что полное число таких подмножеств больше числа имеющихся в системе подмножеств мощности .

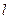Рассмотрим двудольный граф 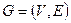, долями которого являются рассматриваемые подмножества мощност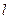и и 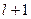, 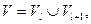а ребрами являются отношения включения подмножеств. От каждой вершины доли 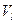отходит 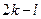ребер, а от каждой вершины доли 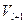- не более 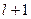ребер. Так как 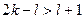, то, подсчитывая число ребер двумя способами, получаем .

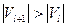Заменяя в системе несравнимых подмножеств подмножества 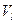на подмножества 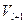, получаем систему из большего числа несравнимых подмножеств. Таким же образом показывается, что максимальная система несравнимых подмножеств не может содержать и подмножеств мощности, большей чем k. Аналогично рассматривается случай .

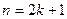Тест

1. Что называется чередующейся цепью? а) цепь, содержащая хотя бы одно ребро паросочетания; б) цепь, содержащая попеременно ребра, входящие и не входящие в паросочетание; в) цепь, начинающаяся и заканчивающаяся вершинами, не покрытыми паросочетанием, и содержащая попеременно ребра, входящие и не входящие в паросочетание.

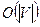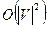2. Трудоемкость решения задачи о паросочетании в двудольном графе равна: а) ; б) ; в) .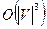

3. Регулярный двудольный граф а) всегда имеет совершенное паросочетание; б) никогда не имеет совершенного паросочетания; в) может иметь, а может и не иметь совершенное паросочетание.

Дата добавления: 2014-01-03