Помехоустойчивое кодирование

Будем считать, что информация закодирована двоичными блоками длины n, которое будем называть кодовыми словами. Пусть эта информация в закодированном виде передается по некоторому каналу связи, где вследствие шумов и помех могут происходить ошибки, в результате которых некоторые единицы становятся нулями и наоборот. Если каждый из 2ⁿ блоков является кодовым словом, как это имеет место, например, в телеграфном коде, то каждая такая ошибка приведет к тому, что одно кодовое слово перейдет в другое и информация дойдет до получателя на приемном конце канала в искаженном виде. Этого можно избежать путем введения некоторой избыточности, когда не все двоичные блоки являются кодовыми словами.

Пусть и 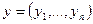- два двоичных набора (блока) длины n. Расстоянием Хэмминга 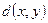между ними называется число позиций, в которых они различаются. Пусть, например, 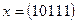, 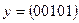. Тогда 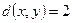, т.к. наборы различаются в первой и четвертой позициях. Расстояние Хэмминга удовлетворяет обычным аксиомам метрики:

1. 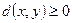, причем 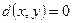тогда и только тогда, когда ;

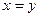2. ;

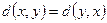3. 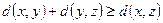(неравенство треугольника).

Шаром Хэмминга радиуса 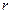с центром в 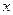будем называть множество наборов 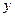таких, что 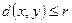. В шаре радиуса 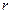содержится 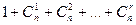наборов.

Пусть теперь кодовые слова выбраны из множества 2ⁿ блоков так, что расстояние между каждой парой слов не меньш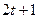е , где 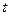– некоторое натуральное число. Тогда, если при передаче слова произошло не более 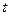ошибок, то их можно исправить по правилу ближайшего соседа: истинное кодовое слово является ближайшим кодовым словом к полученному в результате ошибок блоку. Таким образом, ограниченное число ошибок может быть исправлено и истинное кодовое слово восстановлено.

Вопрос о выборе множества кодовых слов, отстоящих достаточно далеко друг от друга, в принципе может быть решен тривиально. Для этого достаточно дублировать каждый двоичный символ слова 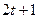раз или столько же раз дублировать все слово. Однако это приведет к росту длины блоков в такое же число раз, что нежелательно. Кодовые слова, находясь на расстоянии не менее 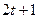друг от друга, должны быть все же «упакованы» достаточно плотно в том смысле, что шары Хэмминга радиуса 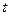с центрами в кодовых словах должны покрывать значительную часть из 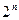блоков, а в идеале покрывать их все, в этом случае код называется совершенным. К сожалению, такая плотная упаковка возможна лишь в исключительных случаях.

Один из основных подходов к построению кодов основан на том, что множество двоичных блоков длины 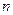рассматривается как множество 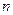– мерных векторов. Сложение векторов осуществляется их покоординатным сложением, причем 0+0=0, 0+1=1+0=1, 1+1=0, т.е. сложение выполняется по модулю 2. Векторы можно также умножать на 1 и 0, при этом умножение на 1 оставляет вектор без изменения, а умножение на 0 делает его нуль – вектором. Скалярное произведение двух векторов есть сумма их покоординатных произведений, приведенная по модулю 2. Таким образом, скалярное произведение также равно 0 или 1. Если скалярное произведение двух векторов равно 0, то говорят, что они ортогональны. Если в определенном таким образом линейном пространстве выбрано некоторое подпространство размерности 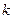, то множество векторов, ортогональных ко всем векторам подпространства, также является линейным подпространством. Которое имеет размерность 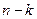и называется подпространством ортогональным к исходному.

Помимо конечности, важным отличием нашего пространства от евклидового является то, что скалярный квадрат вектора, имеющего четное число единиц, оказывается равным нулю, т.е. вектор получается ортогональным самому себе. Поэтому из ортогональности системы векторов не следует их линейной независимости и все пространство может не быть суммой некоторого подпространства и ортогонального ему пространства. Это, однако, не является существенным для наших целей.

Важный класс кодов, называемых линейными, определяется тем, что в линейном пространстве двоичных блоков выбирается некоторое подпространство и его векторы объявляются кодовыми словами. Пусть выбранное подпространство имеет размерность 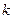. Тогда в нем существует 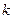линейно независимых векторов (базис) и любой вектор подпространства является их линейной комбинацией. Так как каждый коэффициент линейной комбинации равнее 0 или 1, то всего существует 2^k различных линейных комбинаций, т.е. кодовое подпространство имеет 2^k векторов.

Пусть 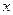,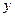– два произвольных слова линейного кода. Прибавив к каждому слово 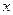(как вектор), получим два других кодовых слова 0 и 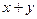. Ясно, чт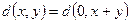о , но 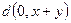равно числу единиц в слове 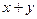. Отсюда следует, что минимальное расстояние между кодовыми словами линейного кода равно минимальному числу единиц ненулевого кодового слова.

Пусть 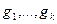- базисные векторы кодового подпространства, 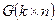- матрица, строками которой являются векторы 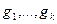. Она называется порождающей матрицей кода. Выбрав в пространстве, ортогональном кодовому, базис 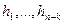, образуем таким же образом матрицу 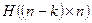,которая называется проверочной матрицей кода. Каждый вектор 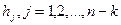, ортогонален каждому из векторов 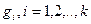. Это может быть записано как 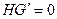, где 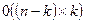- матрица, состоящая из нулей.

Имея проверочную матрицу 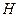, кодовое подпространство можно определить как множество векторов 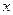, удовлетворяющих соотношению

,

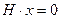где 0 – вектор – столбец из 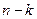нулей.

Опишем теперь прием, позволяющий строить линейный код с минимальным расстоянием 3. Выберем некоторое натуральное число 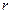и сформируем матрицу 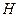так, чтобы все её 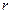столбцов были нулевыми и попарно различными, что всегда возможно при 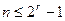. Тогда линейный код с проверочной матрицей 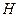будет иметь кодовое расстояние не менее 3, т.к. вектор 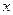, имеющий одну или две единицы не может удовлетворять соотношению 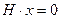. Этот линейный код, способный исправить одну ошибку, называется кодом Хэмминга.

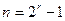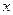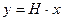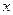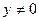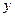Особенно изящной эта конструкция оказывается при . Пусть – произвольное слово (не обязательно кодовое), и пусть . Тогда, если , то является кодовым словом. Если же , то является одним из столбцов матрицы 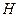, например 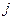– ым. Тогда, инвертировав 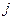– ую координату вектора 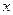, мы получим кодовое слово.

Данное замечание, с одной стороны, позволяет легко исправлять одиночные ошибки, а с другой – показывает, что шары единичного радиуса с центрами в кодовых словах не пересекаются и покрывают все векторы линейного пространства, т.е. код является совершенным.

В качестве примера пусть 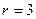, , 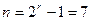тогда проверочная матрица

.

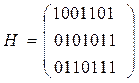Совершенный код Хэмминга длины 7 с проверочной матрицей 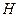содержит 2⁴=16 кодовых слов. Допустим, что на приемном конце канала связи было принято слово 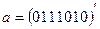. Так как

.

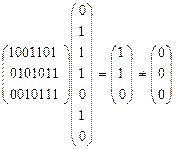то 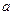не является кодовым словом. В соответствии с допущением, что в канале связи могло произойти не более одной ошибки, восстановим истинное передаваемое по каналу слово. Столбец 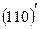является четвертым столбцом матрицы 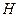. Инвертируя четвертую координату вектора а, получаем, что передавалось кодовое слово.

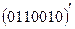Тест

1. Какое минимальное расстояние между кодовыми словами позволяет исправить t ошибок? а) t; б) 2t; в) 2t+1.

2. Сколько имеется кодовых слов в линейном коде с проверочной матрицей 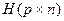? а) 2^р; б)2ⁿ ; в) 2^n-p.

3. Какой код с минимальным расстоянием 2t+1 называется совершенным? а) шары радиуса t не пересекаются; б) шары радиуса t покрывают все двоичные блоки; в) шары радиуса 2t+1 покрывают все двоичные блоки.

Дата добавления: 2014-01-03; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!