Согласно Малой теореме Ферма в поле для любого имеем

Если n – число составное, то кольцо 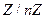не будет полем. В этом случае мультипликативную группу образуют те 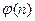элементов из 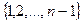, которые взаимно просты с n.

Для любого элемента а мультипликативной группы имеем место 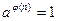, что составляет содержание теоремы Эйлера, обобщающей теорему Ферма на случай произвольного n.

Эффективный метод обращения элементов мультипликативной группы основан на алгоритме Евклида. Пусть требуется найти а ^-1. Так как (а, n)=1, то существуют такие целые k ₁ и k ₂, что 1= k ₁ а+k ₂ n. Тогда 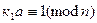, т.е. а ^-1= k ₁.

Выберем в качестве примера n =20. Мультипликативная группа кольца 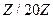состоит из элементов 1, 3, 7, 9, 11, 13, 17, 19. Найдём элемент, обратный к 9, т.е. 9^-1. Для этого применим алгоритм Евклида для нахождения общего делителя чисел 20 и 9 (который равен 1). Делим 20 на 9 с остатком

20=2×9+2.

Делим 9 на 2 с остатком

9=4×2+1.

Полученную в качестве остатка единицу выражаем из последнего равенства через 9 и 2 и подставляем вместо двойки её выражение из первого равенства

1=9-4×2=9-4(20-2×9)=9×9- 4×20.

Таким образом, элемент 9 оказался обратным сам себе 9^-1=9.

Если а – примитивный корень по простому модулю р, то каждый ненулевой элемент поля 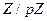может быть единственным образом представлен в ви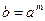де , где 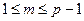. Число m называется дискретным логарифмом элемента b по основанию а. Дискретный логарифм является функцией, обратной по отношению к функции возведения в степень.

Есть, однако, существенная разница между двумя функциями с вычислительной точки зрения. Для вычисления а ^m достаточно сделать не более 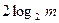умножений, т.е. трудоёмкость пропорциональна числу десятичных знаков числа m. Пусть, например, требуется вычислить а ⁵³. Вместо того, чтобы делать 52 умножения, поступим следующим образом. Представим число 53 в двоичной записи 53=2⁵+2⁴+2²+1 и возведём в степень по формуле

,

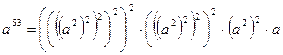которая требует всего лишь 5+3=8 умножений.

Для дискретного логарифма подобного эффективного приёма не известно, и его вычисление представляет собой трудную задачу, которая оказывается не под силу даже современным компьютерам, если р - число с более чем 200 десятичными знаками.

Другая алгоритмически трудная задача в теории чисел – это разложение числа на простые множители. Существуют эффективные методы проверки числа на простоту, полиномиальной трудоёмкости от длины записи числа в позиционной системе счисления. Однако, если число оказывается не простым, то найти его разложение на простые множители может оказаться невозможным даже с помощью самого мощного современного компьютера, если это число с более чем 200 десятичными знаками. Эффективного алгоритма для решения этой задачи не известно, хотя и не доказано, что его не существует. Положение не улучшается даже в том случае, когда известно, что число разлагается на два простых множителя.

На алгоритмической трудности задач нахождения дискретного логарифма и разложения на множители и основана современная криптография, позволяющая избежать процедуры предварительного обмена ключом.

Современная криптография. Рассмотрим две известные криптографические системы, позволяющие избежать предварительного распространения ключа – это система с открытым распространением ключа и система с открытым ключом. В системе с открытым распространением ключа два корреспондента вырабатывают общий секретный ключ, пользуясь открытым каналом связи. При этом третье лицо, перехватывая все общения по данному каналу, тем не менее не в состоянии получить ключ. Это «чудо», предложенное Диффи и Хеллменом, основано на алгоритмической сложности вычисления дискретного логарифма.

В системе с открытым ключом каждый пользователь имеет два собственных ключа: открытый для зашифровывания и секретный- для расшифровывания. Ключ для зашифровывания помещается в открытый файл и любой, желающий отправить секретное сообщение данному лицу, может им воспользоваться. Расшифровать же данное сообщение способно только само лицо, т.к. лишь оно имеет ключ для расшифровывания. Хотя, в принципе, найти ключ для зашифровывания возможно, алгоритмическая трудность этой задачи не позволяет решить её в приемлемое время. Среди систем с открытым ключом наибольшее распространение получила система RSA, названная так в честь своих создателей (Rivest, Shamir, Adleman, 1978). Система RSA основана на алгоритмической трудности разложения числа на простые множители.

Опишем сначала систему Диффи и Хеллмана с открытым распространением ключа. Группа пользователей помещает в открытый файл простой модуль р (очень большое число) и примитивный корень a поля 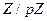. Затем каждый пользователь выбирает число 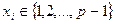, которое хранит в секрете, вычисляет 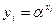и помещает 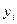в открытый файл. Если пользователи i и j хотят обменяться сообщениями, они используют в качестве ключа 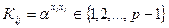. Пользователь i берёт 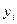из открытого файла и вычисляет 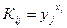. Пользователь j берёт y _i из открытого файла и вычисляет.

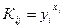Двоичная запись ключа 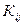может быть теперь использована двумя пользователями в качестве двоичной ленты для побитового сложения с сообщением.

Перехватчик, зная y _i и y _j, может, в принципе, найти х _i и x _j и получить ключ 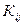, но алгоритмическая трудность вычисления дискретного логарифма не позволяет сделать это в приемлемое время. Если же эффективный алгоритм для вычисления дискретного логарифма будет найден, то эта криптографическая система рухнет.

Обратимся теперь к системе RSA. Каждый пользователь выбирает два больших простых числа 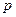и 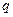, которые хранит в секрете, и находит 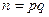. Функция Эйлера 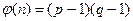. Затем пользователь выбирает 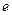, взаимно простое с 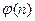, и находит ему обратное по модулю 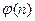, т.е. такое 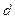, что 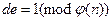. Пользователь помещает 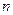и 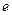в открытый файл, а 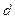хранит в секрете.

Кодовым алфавитом в системе RSA является множество 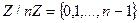. Открытый текст переводится в двоичную последовательность, которая разбивается на блоки, кодируемые символами алфавита 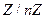. Зашифровывание сводится к перестановке на множестве символов 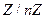, расшифровывание - к обратной перестановке. Вскрытие шифра с помощью частотного анализа здесь оказывается невозможным из-за огромного объёма алфавита .

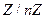Пусть 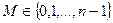- кодовое слово открытого текста. Соответствующее слово шифротекста 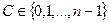вычисляется с помощью имеющегося в открытом файле числа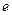

.

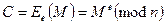Обратное преобразование осуществляется с помощью хранимого пользователем в секрете числа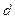

.

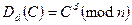Покажем, что результатом обратного преобразования будет исходное кодовое слово открытого текста

.

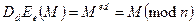Так как 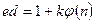,то

.

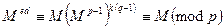Последнее сравнение следует из Малой теоремы Ферма.

Аналогично

.

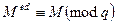Отсюда следует, что

.

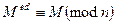Факт существования обратного преобразования доказывает, что зашифровывающее преобразование действительно является перестановкой на множестве символов .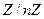

Не известно эффективного способа нахождения секретного расшифровывающего ключа 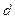по открытому зашифровывающему ключу 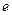без знания разложения числа 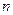на простые множители. Этим и обуславливается криптографическая стойкость системы RSA.

Системы с открытым ключом типа RSA, наряду с несомненным удобством для пользователей, обладают, на первый взгляд, и существенным недостатком. А именно, каждый может воспользоваться открытым ключом определенного лица и от его имени послать зашифрованное сообщение. Если банк получает по электронной почте от своего клиента зашифрованное сообщение с распоряжением, касающимся управления финансовым вкладом клиента, то он должен быть уверен в подлинности авторства сообщения при осуществлении с вкладом требуемых операций. В случае письменного распоряжения его аутентичность подтверждается личной подписью клиента. Подобное подтверждение в случае распоряжения, посланного по электронному каналу связи, называется электронной подписью.

В системе RSA проблема электронной подписи может быть решена просто. Пусть 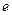– открытый зашифровывающий ключ банка, 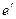- открытый зашифровывающий ключ клиента, а 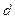и 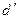соответственно – их секретные расшифровывающие ключи. Для доказательства аутентичности клиенту достаточно зашифровать открытый текст М с помощью оператора 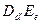, что дает шифротекст

,

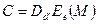а банку для расшифровывания следует воспользоваться оператором 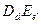. Так как 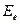и 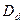, а также 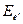и 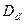- пары взаимно обратных операторов, то

.

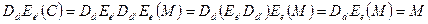Этим приемом в системе RSA может быть обеспечена как секретность, так и аутентичность. Подтверждением аутентичности служит зашифровывающий оператор 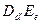, в состав которого входит оператор 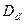, являющийся личным секретом клиента.

Тест

1. Что такое «ключ»? а) Алгоритм зашифровывания; б) Алгоритм расшифровывания; в) Сменный элемент шифра, обеспечивающий поддержание секретности.

2. Совпадают ли зашифровывающий и расшифровывающий ключи? а) Совпадают; б) Не совпадают; в) Не совпадают в системе с открытым ключом.

3. Что обуславливает криптографическую стойкость системы RSA? а) Трудность нахождения дискретного логарифма; б) Трудность разложения на множители; в) Трудность нахождения обратного элемента в мультипликативной группе кольца .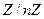

Итоговый тест

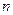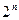1. Сколько подмножеств у n – мерного множества? а); б) ; в) .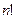

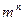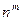2. Чему равна мощность прямого произведения n – мерного и m – элементного множеств? а) ; б) ; в) .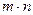

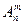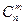3. Cколько m – элементных подмножеств у n – элементного множества? а) ; б) ; в) .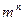

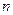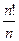4. Сколькими способами можно рассадить n человек за круглым столом? (Два способа считаются одинаковыми, если каждый имеет тех же двух соседей, неважно с какой стороны). а) ; б) ; в) .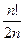

5. Цикл называется гамильтоновым, если он а) проходит через каждое ребро; б) проходит через каждую вершину; в) через каждую вершину проходит один раз.

6. Алгоритм в дискретной математике считается эффективным, если а) всегда приводит к решению; б) может быть реализован на компьютере; в) имеет полиномиальную от размерности задачи трудоемкость.

7. Чему равно минимальное расстояние между кодовыми словами линейного кода? а) минимальному числу единиц нулевого кодового слова; б) числу строк порождающей матрицы; в) числу строк проверочной матрицы.

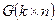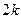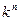8. Число кодовых слов у кода с порождающей матрицей равно а) ; б) ; в) .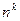

9. Что обеспечивает криптографическую стойкость системы с открытым распространением ключа? а)трудность нахождения дискретного логарифма; б)трудоемкость разложения на множители; в)трудоемкость нахождения обратного элемента в мультипликативной группе кольца .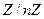

10. Почему в современных криптографических системах типа RSA невозможно вскрытие шифра с помощью частотного анализа? а) из – за объема необходимых вычислений; б) из – за трудностей программирования; в) большая длина участков открытого текста, зашифровываемая одним блоком, практически исключает повторяемость блоков шифротекста.

Рекомендуемая литература

Основная

1. Андерсон Д.А. Дискретная математика и комбинаторика. – М.: «Вильямс», 2003.

2. Аршинов М.Н., Садовский Л.Е. Коды и математика. – М.: «Наука», 1983.

3. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: «Наука», 2004.

4. Дориченко С.А., Ященко В.В. 25 этюдов о шифрах. – М.: «ТЕИС», 1994.

5. Зуев Ю.А., Садыкова А.Р. Математика логика и теория алгоритмов. Теория множеств. Дискретная математика. – М.: МГУТУ, 2004.

6. Иванов Б.Н. Дискретная математика. Алгоритмы и программы. – М.: «Лаборатория Базовых Знаний», 2002.

7. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: «МАИ», 1992.

Дополнительная

1. Емеличев В.А., Мельников О.И., Сарванов В.И., Тышкевич Р.И. Лекции по теории графов. – М.: «Наука», 1990.

2. Кнут Д.Э. Искусство программирования. Том 1. Основные алгоритмы. – М.: «Вильямс», 2000.

3. Мак – Вильямс Ф.Дж., Слоэн Н.Дж.А. Теория кодов, исправляющих ошибки. – М.: «Связь», 1979.

4. Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность.- М.: «Мир», 1985.

5. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика.- М.: «Мир», 1980.

6. Харари Ф. Теория графов. – М.: «Мир», 1973.

7. Штайнер Б. Прикладная криптология. – М.: «Триумф», 2002.

Словарь основных терминов

1. Гамильтонов граф – граф, имеющий гамильтонов цикл.

2. Гамильтонов цикл – цикл, проходящий по одному разу через каждую вершину графа.

3. Граф – конечное множество элементов, называемых вершинами, с выделенным подмножеством неупорядоченных пар элементов, называемых ребрами.

4. Двудольный граф – граф, множество вершин которого можно разбить на 2 пересекающиеся подмножества так, что каждое ребро имеет одну вершину из одного подмножества, а другую – из другого.

5. Дерево – связный граф без циклов.

6. Ключ – сменный элемент шифра, периодическое изменение которого обеспечивает поддержание секретности.

7. Криптография – тайнопись.

8. Лес – граф без циклов.

9. Ориентированный граф (орграф) – конечное множество элементов, называемых вершинами, с выделенным подмножеством упорядоченных пар элементов, называемых дугами.

10. Остовной подграф графа 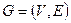– граф 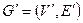, у которого , .

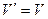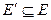11. Паросочетание – подмножество ребер графа такое, что каждая вершина графа инцидентна не более чем одному ребру из подмножества.

12. Подграф графа 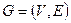– граф 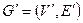, у которого , .

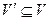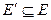13. Регулярный граф – граф, все вершины которого имеют одинаковую степень.

14. Сеть – ориентированный граф с двумя выделенными вершинами – истоком и стоком и с заданными на дугах пропускными способностями.

15. Степень вершины – число инцидентных ей ребер.

Ответы к тестам

1 2 3 4 5

1.1	б	б	в	в	б
1.2	в	б	б
1.3	а	б	в	в
1.4	в	б	в	а	в
1.5	а	б	в
1.6	а	а	а
2.1	в	в	б
2.2	а	в	б
2.3	в	в	б
2.4	в	б	а
2.5	в	б	а
2.6	в	в	а
2.7	б	в	б
3.1	б	б	б
3.2	в	в	б
3.3	в	в	б

Зуев Юрий Анатольевич

Дискретная математика

Курс лекций

Подписано к печати:

Тираж:

Заказ №:

Дата добавления: 2014-01-03