Имитационный способ представления задачи 1

При имитационном способе решения обязательным является наличие некоего счётчика, который позволяет моделировать процесс по шагам или по деталям процесса.

а)Имитационный алгоритмический способ

Повторяя пошагово расчёт в цикле, на каждом этапе работы алгоритма будем имитировать течение процесса (рис. 1.16). Обратите внимание, что процесс берётся не в целом, а как бы в деталях, по шагам. Переменная t является координатой, а значит, отслеживается счётчиком с шагом h. Идея имитации — продвигать пешехода и велосипедиста на величину V · h на каждом такте, где h — достаточно малая величина. Поскольку мы рассматриваем множество актов движения по отдельности, можно по ходу менять все переменные модели, например, V. Остановка процесса имитации определяется суммой путей, пройденных велосипедистом и пешеходом навстречу друг другу, и сравнением её с расстоянием S.

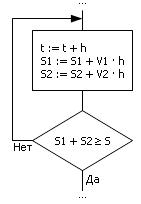
Рис. 1.16. Блок-схема решения задачи о встрече
(имитационный алгоритмический способ)

б) Имитационный геометрический способ

Решение может быть найдено геометрически. Для этого в осях (t, S) схемой, показанной на рис. 1.17, строятся траектории движения объектов.

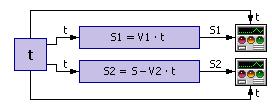
Рис. 1.17. Схема решения задачи о встрече
(имитационный геометрический способ)

На рис. 1.18 вы видите картину, образованную двумя осциллограммами. Точка, в которой пересекаются осциллограммы, является предполагаемой точкой встречи двух объектов.

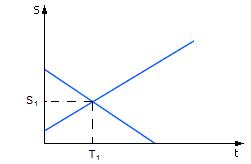
Рис. 1.18. Вид решения задачи о встрече
(имитационный геометрический способ)

в) Имитационная статистическая постановка задачи

Главное отличие имитационных моделей от аналитических, которые мы рассмотрели выше, состоит в том, что имитационную модель можно постепенно усложнять, при этом результативность модели не падает.

Усложним задачу 1, введя в неё дополнительное условие. Представим, что на пути первого и/или второго объекта встретится помеха — пусть это будет участок железной дороги со шлагбаумом, который работает по случайному закону. Если шлагбаум открыт, то объект может переходить железную дорогу, в противном случае он не имеет права этого делать

Промоделировать случайную работу шлагбаума можно с помощью генератора случайных чисел (ГСЧ). В различные моменты времени ГСЧ будет выдавать случайное число r = 0 или r = 1, это будет означать, что шлагбаум закрыт или, соответственно, открыт (см. рис. 1.19).

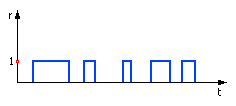
Рис. 1.19. Вид функции случайных помех
(к задаче о встрече)

Частоту открывания шлагбаума можно контролировать, увеличивая или, наоборот, уменьшая число q, пересчитав случайное число r в z по формуле: z:= ed(q – r).

На рис. 1.20 дана иллюстрация усложнённой задачи 1.

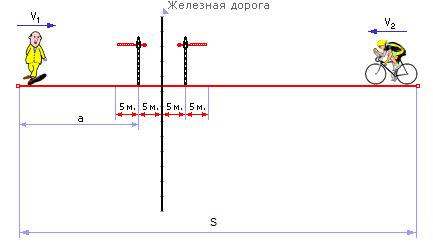
Рис. 1.20. Иллюстрация к усложнённой задаче о встрече

Итак, подведём итог.

Модель - способ замещения реального объекта, используемый для его исследования, когда натуральный эксперимент невозможен, дорог, опасен, долговременен.

Примеры. Поскольку исследование Луны небезопасно для человека, для этой цели используют луноход как модель исследователя; поскольку реальные эксперименты над экономикой страны дороги по своим последствиям, то используют математические модели экономики для изучения последствий управляющих решений; поскольку процесс обработки металлов взрывом скоротечен во времени, то его изучают на модели в увеличенном масштабе времени, а процесс коррозии — в уменьшенном; атом изучается в увеличенном масштабе пространства, а космогонические процессы - в уменьшенном масштабе пространства; поскольку при проектировании объекта его попросту не существует, то исследование будущих свойств объекта ведётся на модели.

Модель несёт системообразующую и смыслообразующую роль в научном познании. На модели изучают неизвестные свойства предметов. Модель стремится как можно более ярко выразить структуру явления, его главные аспекты. Модель является концентрированным выражением сущности предмета или процесса, выделяя только его основные черты.

Знания - это модели окружающего мира, фиксируемые человеком в его мозгу или на технических носителях. Модели обладают повышенной наглядностью, выделяя главные аспекты сущности, и активно используются в процессах познания и обучения. Человек, решая, как ему поступить в той или иной ситуации, всегда пытается представить себе последствия решения, для этого он проигрывает ситуацию, представляет её себе мысленно, строя модель в голове. Компьютер является усилителем для производства данной деятельности, инструментом информационной технологии. Компьютерные модели ускоряют процесс исследования, делают его более точным.

Алгоритмы - знания, выстраиваемые человеком (или, шире, разумным существом) в цепочку так, чтобы соединить исходное состояние с желаемым, целью; это один из вариантов ряда мероприятий, шагов, приводящих к цели.

Таким образом, модели - это основа разумной мыслительной деятельности; модели играют роль базиса, а моделирование — роль инструмента для прогнозирования.

Процесс моделирования состоит из трёх стадий: формализации (переход от реального объекта к модели), моделирования (исследование и преобразования модели), интерпретации (перевод результатов моделирования в область реальности).

Модель есть зависимость F между входом X и выходом Y. Модель отражает закономерность Y = F (X). Часто модель является законом. Модель верна в рамках допущенных при её построении гипотез. Поэтому модель ограничена некоторой областью и адекватна в ней.

Набор моделей образует научную дисциплину (механика, физика, горное дело и т. д.) Модель может быть расширена путём учёта в ней дополнительных параметров. Тогда область её применения становится шире.

Объект может быть представлен в виде аналитической или имитационной модели.

Аналитическое представление подходит лишь для очень простых и сильно идеализированных задач и объектов, которые, как правило, имеют мало общего с реальной (сложной) действительностью, но обладают высокой общностью. Аналитические модели обычно применяют для описания фундаментальных свойств объектов (поэтому ими так широко пользуется теоретическая физика), так как фундамент прост по своей сути. Сложные объекты редко удаётся описать аналитически.

Имитационное моделирование позволяет разлагать большую модель на части (объекты, «кусочки»), которыми можно оперировать по отдельности, создавая другие, более простые или, наоборот, более сложные модели. Таким образом, имитационное моделирование тяготеет к объектно-ориентированному представлению, которое естественным образом описывает объекты, их состояние, поведение, а также взаимодействие между ними. Имитационную модель можно постепенно усложнять и усложнять; аналитический способ этого не допускает или допускает, но с большими ограничениями.

Модель может быть соединена с другими моделями. Математически это означает совместное решение моделей (пересечение) и наложение тождеств на связываемые переменные. При связывании модели образуют систему, которая имеет определённую структуру (вложенную, параллельную, последовательную, смешанную, с обратными связями и т. д.)

Если к построенной модели добавить вопрос, то с помощью неё можно решить задачу, получить ответ, который заранее не очевиден. Если ответ заранее очевиден, то модель не строят. Обычно одна и та же модель годится для решения множества задач. Решая задачи, человек обычно строит модели в своей голове и оживляет (интерпретирует) их там же или на искусственном носителе (в среде моделирования).

Повторим:

модель + вопрос + дополнительные условия = задача.

В виде условий могут быть любые дополнительные выражения: равенства, присваивания начальных данных, неравенства, цели, функционалы и т. д., имеющие смысл ограничений, условий, дополнительных связей.

В виде вопроса может служить одна (или несколько) из неизвестных переменных.

Задача доопределяет свободные переменные модели, сужает область возможных решений.

Задачи, решаемые на модели, делятся на прямые и обратные. Прямые задачи по заданному X находят Y путём подстановки X в уравнение Y = F (X). Обычно такие задачи называют задачами анализа. Обратные задачи по заданному Y находят X путём нахождения обратной функции F ^–1 и подстановки X = F ^–1(Y). Обычно их называют задачами синтеза. Если найти обратную функцию F ^–1 в явном виде затруднительно, то составляют вычислительные схемы для численного определения X. Часто к этому виду приводятся задачи управления объектами.

Ещё одной специфической задачей является нахождение по заданным X и Y зависимости F или её коэффициентов. Это задача построения (или настройки) модели.

Дата добавления: 2014-01-03