Полный факторный эксперимент (ПФЭ)

Систем

Методы планирования эксперимента с моделями

Основная задача планирования машинных экспериментов заключается в получении необходимой информации об исследуемой системе при ограниченных ресурсах (затраты машинного времени, памяти и т.п.). К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, уменьшения погрешности результатов моделирования, проверки адекватности модели и т.п.

Эффективность машинных экспериментов существенно зависит от выбора плана эксперимента, т.к. именно план определяет объём и порядок проведения вычислений на ЭВМ, приёмы накопления и статистической обработки результатов моделирования системы. Поэтому основная задача планирования машинных экспериментов с моделью формируется следующим образом: необходимо получить об объёме моделирования, заданном в виде моделирующего алгоритма (программы) при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования.

Таким образом, при машинном моделировании необходимо не только рационально планировать и проектировать саму модель системы, но и процесс её использования, т.е. проведения с ней эксперимента.

При планировании машинных экспериментов возникает целый ряд проблем, взаимно связанных как с особенностью функционирования моделируемого объекта, так и с особенностью машинной реализации модели и обработки результатов эксперимента. В первую очередь к таким относятся проблемы построения плана машинного эксперимента, стохастической сходимости результатов, ограниченности машинных ресурсов, уменьшения дисперсии оценок, полученных на машинной модели и т.д.

Рассмотрим основные понятия теории планирования эксперимента. Исследуемый объект (над которым проводится эксперимент) будем представлять в виде модели «черного ящика» с входами 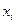и выходами .

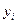Цель эксперимента - изучение влияния переменных 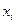на 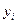. Входы 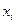называются факторами (независимые, экзогенные переменные); выходы 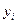- реакция/отклик (параметр оптимизации, целевая функция, эндогенные переменные).

Фактор может принимать одно из нескольких значений-уровней. Фиксированный набор уровней факторов определяет одно из возможных состояний системы и представляет собой условия проведения одного из возможных опытов одного эксперимента - точка в факторном пространстве. Факторное пространство - это координатное пространство, на осях которого откладывают значения исследуемых факторов. Если перебрать все возможные наборы состояний системы, то мы получим полное множество состояний - число возможных опытов. Математическая модель объекта - это функциональная зависимость

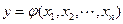, (2.14)

которая называется функцией отклика, а ее геометрический образ - поверхностью отклика.

В общем случае, когда исследование модели ведется при неполном знании механизма изучаемых явлений, аналитическое выражение функции (2.14) неизвестно. Наибольшее в этом случае применение нашли модели в виде полиномов

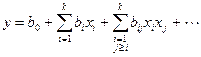(2.15)

с теоретическими коэффициентами регрессии . Функция отклика может иметь и более сложную зависимость от факторов. Некоторые из них удается привести к линейному виду. Такими моделями являются мультипликативная регрессионная, экспоненциальная и др. Если выбрана модель планирования, т.е. выбран вид функции (2.15) и записано уравнение, то остается спланировать и провести эксперимент для оценки числовых значений коэффициентов этого уравнения.

План эксперимента, позволяющий вычислить коэффициенты линейного уравнения регрессии, называют планом первого порядка. План эксперимента, позволяющий вычислить коэффициенты полного уравнения регрессии 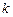-й степени, будет планом 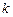-го порядка.

Каждый фактор 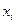меняется в определенном диапазоне 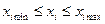, а фактически принимает ряд 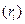значений из этого диапазона. Общее число возможных экспериментов дается соотношением

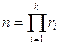, (2.16)

а при одинаковом значении фиксированных значений (уровней) для всех факторов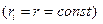

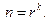(2.17)

Эксперимент, при котором реализуются все возможные сочетания факторов, принято называть полным факторным экспериментом (ПФЭ). Из выражения (2.17) следует, что в многофакторных задачах при нескольких фиксированных уровнях факторов общее число экспериментов оказывается чрезвычайно большим. На практике обычно используют планы, предусматривающие фиксирование всех факторов на двух (планы 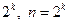) или, существенно реже, на трех (планы 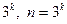) уровнях.

При составлении плана ПФЭ 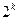для каждого фактора выбирается нулевой (базовый) уровень 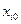, соответствующий центру эксперимента. Обычно, но не обязательно, он выбирается в центре диапазона варьирования:

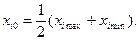
Выбирается шаг варьирования 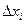, характеризующий отклонение фактора от нулевого уровня. Эксперимент проводится при двух значениях факторов 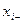и :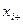

.

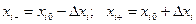Шаг варьирования выбирается на основе опыта и интуиции исследователя и обычно составляет

.

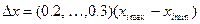Для облегчения расчетов удобно провести нормировку факторов с

помощью преобразования

.

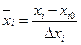При этом нижнее и верхнее значение фактора 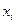равны -1 и +1:

.

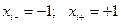Расположение экспериментов при планировании 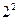показано на рис.2.9, а соответствующая матрица планирования приведена в табл.2.3.

Строки матрицы соответствуют различным экспериментам, а столбцы значениям факторов. Для упрощения и унификации записи условий экспериментов и облегчения обработки данных в матрицах планирования обычно вместо -1 и +1 записывают: на нижнем уровне «-» и на верхнем уровне «+».

Планирование 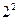позволяет определить четыре коэффициента уравнения регрессии. Модель может быть представлена в виде неполного квадратного уравнения, включающего свободный член, линейные эффекты и эффект двойного взаимодействия факторов

.

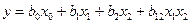В табл.3.1 добавлен столбец фиктивной переменной 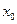, необходимый для оценки свободного члена .

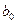План, в котором число экспериментов равно числу определяемых коэффициентов, называется насыщенным.

После реализации плана получают 4 уравнения с 4 неизвестными, их решение и даст оценку всех 4 коэффициентов уравнения регрессии .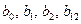

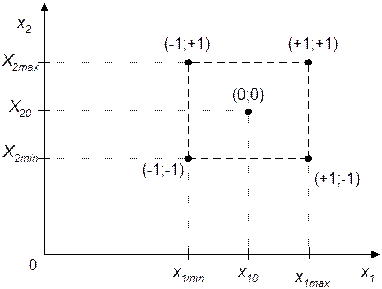
Рис.2.9. План эксперимента

Таблица 2.3

Матрица планирования полного факторного эксперимента

для двух факторов

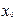
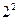
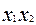
№ эксперимента		План ПЭФ		Отклик y
	+	–	–	+
	+	+	–	–
	+	–	+	–
	+	+	+	+

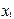
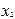
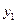
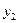
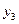
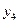
Пример. Одна из основных целей в теории эксперимента - это оптимальное использование факторного пространства.

Проиллюстрируем идею на простом примере - задаче о взвешивании трех объектов A, B, C. Традиционно эксперимент проводится по следующей схеме:

№ опыта	A	B	C	Результат взвешивания
	-	-	-
	+	-	-
	-	+	-
	-	-	+

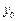
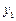
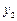
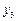
где «+» - объект положен на весы; «-» - объект отсутствует на весах.

Сначала проводится «холостое» взвешивание — определяется нулевая точка весов, затем по очереди взвешиваются все объекты. Это пример однофакторного эксперимента - здесь изучается поведение каждого фактора в отдельности. Вес определяется по результатам двух опытов:

.

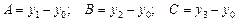Дисперсия результатов взвешивания:

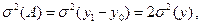
где 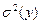— дисперсия ошибки взвешивания.

Рассмотрим другую схему проведения эксперимента.

№ опыта	A	B	C	Результат взвешивания
	+	-	-
	-	+	-
	-	-	+
	+	+	+

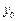
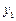
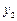
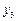
Вес каждого тела определяется по формулам:

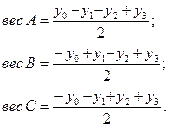
В числители стоят элементы последнего столбца со знаками, указанными в соответствующих столбцах А, В, С. Мы видим, что при вычислении, скажем, веса А он входит в числитель два раза, и поэтому в знаменателе стоит число 2. Вес объекта А, вычисленный по приведенной выше формуле, оказывается неискаженным весами объектов В и С, так как вес каждого из них входит в формулу для веса объекта А дважды и с разными знаками.

Дисперсия результатов взвешивания по новой схеме

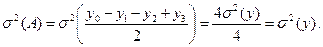
При новой схеме взвешивания дисперсия вдвое меньше, хотя в каждом случае выполнялось по четыре эксперимента.

Увеличение точности эксперимента в два раза происходит по той причине, что в первом случае вес определялся по результатам двух экспериментов, во втором случае - по результатам всех четырех.

Вторая схема эксперимента — многофакторная: здесь оперируют всеми факторами так, чтобы каждый вес вычислять по результатам всех опытов, проведенных в данной серии экспериментов.

Матрица ПФЭ обладает следующими свойствами:

a) Свойство симметричности: алгебраическая сумма элементов вектор - столбца каждого фактора равна нулю (за исключением столбца, соответствующему свободному члену)

,

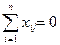где i – номер фактора; j – номер эксперимента.

b) Свойство нормирования: сумма квадратов элементов каждого столбца равна числу опытов

.

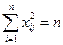c) Свойство ортогональности; скалярное произведение всех вектор – столбцов (сумма почленных произведений элементов любых двух векторов – столбцов матрицы) равно нулю

.

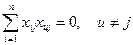d) Рототабельность матрицы, т.е все точки в матрице планирования подбираются так, чтобы точность предсказания значений параметра оптимизации была одинакова на равных расстояниях от центра эксперимента и не зависела от направления.

Планы, для которых выполняется условие (с), называются ортогональными. Благодаря этому свойству резко уменьшаются трудности, связанные с расчетом коэффициентов уравнения регрессии.

Поскольку результаты наблюдений носят случайный характер, то для повышения точности результатов целесообразно при каждом сочетании факторов проводить не один, а несколько экспериментов и в качестве выходного значения функции отклика принимать их среднее. План такого эксперимента для случая двух факторов и трех экспериментов приведен в табл.2.4.

Таблица 2.4

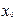
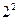
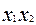
Номер эксперимента		План ПЭФ		Результат	Среднее
	+	–	–	+
	+	+	–	–
	+	–	+	–
	+	+	+	+

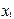
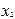
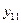
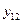
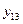
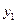
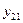
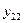
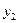
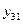
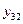
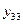
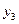
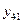
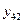
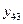
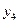
Порядок проведения всех (в данном случае 12-ти) экспериментов должен быть рандомизирован, т.е. определен с помощью таблицы случайных чисел, что позволяет исключить влияние временного дрейфа характеристик исследуемой системы. Делается это следующим образом. Выбирается произвольный участок таблицы случайных чисел, и последовательно просматриваются его строки или столбцы с любого места. Последовательность (очередность) проведения экспериментов назначается в соответствии с очередностью появления чисел 1, …,N при просмотре участка таблицы. Числа, большие по значению, чем номера экспериментов, пропускаются. Повторяющиеся числа учитываются лишь первый раз, а далее также пропускаются.

Переход к планированию 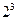требует двукратного повторения планирования 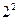, причем в первом случае 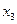поддерживается на нижнем, а во втором на верхнем уровне (рис.2.10). Матрица планирования приведена в табл. 2.5.

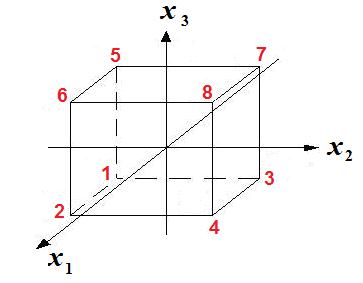
Рис. 2.10. План эксперимента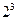

Таблица 2.5

Матрица планирования полного факторного эксперимента

для трех факторов

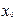
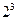
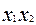
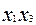
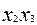
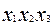
Номер эксперимента		План ПЭФ					Реакция y
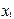
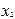
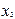
	+	-	-	-	+	+	+	-	y1
	+	+	-	-	-	-	+	+	y2
	+	-	+	-	-	+	-	+	y3
	+	+	+	-	+	-	-	-	y4
	+	-	-	+	+	-	-	+	y5
	+	+	-	+	-	+	-	-	y6
	+	-	+	+	-	-	+	-	y7
	+	+	+	+	+	+	+	+	y8

Модель может быть представлена в виде

.

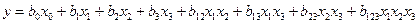И включает в себя свободный член, линейные эффекты, эффекты двойного взаимодействия и эффекты тройного взаимодействия.

Аналогично можно построить матрицы планирования 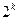для задач большей размерности. При этом дважды повторяется планирование меньшей размерности 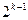, причем первый раз новый фактор берется на нижнем, а второй раз на верхнем уровне.

Для компактной записи плана эксперимента, а также отдельных экспериментов используются буквенное обозначение – код эксперимента. Каждому из варьируемых факторов сопоставляется буква латинского алфавита 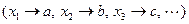, и в буквенное обозначение выносятся буквы, соответствующие факторам, находящимся на верхнем уровне.

Так, для факторов планирования 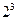код ab указывает на то, что на верхнем уровне заданы факторы 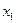и 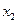, а фактор 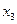находится на нижнем уровне. Код bc означает, что фактор 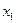находится на нижнем уровне, а факторы 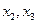- на верхнем уровне. Для эксперимента, где все факторы заданы на нижнем уровне, используется обозначение (1).

Полные факторные эксперименты 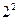и 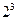можно задать кодами

(1), a, b, ab;

(1), a, b, ab, c, ac, bc, abc.

Дата добавления: 2014-01-03